《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第5章 根据边值观点的电准静态场

第5章根据边值观点的电准静态场5.0 引言在第4章中，我们讨论了电准静态场定律。电场强度E是无旋的，且可用电位梯度的负值表示E=-@(1)如果电位@通过泊松方程与电荷密度β相联系vo=-.(2)那么高斯定律就能满足。在无电荷的空间区域中，@服从拉普拉斯方程，即β=0时的式(2)。第 4章的最后部分我们致力于用“机会主义的”方法求边值问题的解。在4.8 节中描述的导致用场源叠加的方法求边值问题解的数值方法则是一个例外。在这一章中将用更直接的方法求解逆值问题，不必借助于数值方法。这是一种不仅作为极化与传导的效应加于EQS定律而有广泛应用的方法，而且在处理MQS系统时也是如此对于那些熟悉用常微分方程描述线性电路动力学的人们又一次存在着有用的类比。当把时间作为自变量时，对于在t=0时接通的激励的响应，可有两种方法去确定。第一种方法是把响应表示成许多冲激响应的叠加。最后所得到的卷积积分代表了t=0之前、之后甚至！-0时全部时间的响应。这与第4章第一部分中所持观点相似。第二种方法根据初始条件描述了在t=0以前的动态特性的厉史。如果所关心的只是t一0之后的时间，那么响应可分成“特殊的”和"齐次的”两部分。描述电路的微分方程的特解不是唯一的,但能保证我们所关心的时间范围内每一磷间，都能满足微分方程。这一特解不必满足初始条件。在这一章中，“激励"是电荷密度，特定的电佗响应保证泊松方程式(2)，在所关心的空间区域中处处满足。在电路的类比中，齐次解用来满足初始条件。在场的问题中，齐次解用来满足边界条件。在一个电路中,齐次解可以认为是对发生在t=0时刻前(在讨论的时闻范围之外)的激励的响应。在确定电位分布时,齐次的响应是由拉普拉斯方程,β=0 时的式(2)所预计的，并可认为或者是由位于所关心区域之外的虚设电荷引起的，或者是感应在边界上的面电荷引起的。在5.1一5.3节中这些观点的展开是自成体系的，并不依赖于对电路理论的熟知。然而，对于那些熟悉常微分方程解答的人，看到在这里处理偏微分方程所用的方法，是过去用以处理常微分方程方法的一种自然的延伸，将感到满意。虽然特解常常能更简单地用其他方法求得，但它直是由重叠积分得来的。因此，本章主要.110

讨论的是齐次解的确定，即求拉普拉斯方程的解。许多实际的结构具有可通过令三维坐标系中的一个坐标变量等于常数来描述的边界。例如，具有矩形横截面盒子的各个面可通过令一个笛卡儿坐标为常数来描述边界。类似地，一个圆柱体的边界自然地应用圆柱坐标系来描述。因此，我们将对自然地“符合”这些构形的拉普拉斯方程的解发生强烈的兴趣。讨论中将穿插许多例子，本章的大部分篇幅用来编列这些解答。。这些结果在本章中是用来描述自由空间中EQS场的。然而，当极化和传导的效应被补充到EQS的范围，以及考虑具有磁化和传导的MQS系统时，本章所建立的拉普拉斯方程的齐次解将是一种频繁应用的方法回顾第4章将识别许多拉普拉斯方程的解。只要场源在讨论区域之外，求出的电位就满足拉普拉斯方程。那么本章将要确定的解答有什么不同呢，从4.8节中采用的满足任意边界条件的数值过程可得到一些启发。在4.8节中，用N个拉普拉斯方程解的叠加来满足边界上N个点的条件。遗憾的是，为了确定这N个解的幅值，必须解N个方程求出N个未知量。本章求出的拉普拉斯方程的解也可弱来作为满足任意边界条件的一个无穷级数中的各项，但是在这一级数中各项的不同之处，是它们的正交性。解答的这一性质使直接确定这个级数中各项的幅值成为可能。通过对傅里叶分析的介绍，函数正交性的概念可能已很熟悉。总之，有关的基本概念将在5.5节中介绍。5.1泊松方程与拉普拉斯方程的特解和齐次解假设我们想要分析如图5.1.1所示的电准静态的情况。在我们关心的用休积V表示的部分空间中已规定了电荷分布 p(r)。这一区域由规定了形状和位置的理想导体所界定。施加在这些导体和封闭面上的电位是已知的，封闭面可以在无限远处。图5.1.1其中可能有电有冷布的间新关心的体积为了说明其上电位受约东的边界而，图中示出了n个隔离的表面和一个包鼠体积的闭合面。在导体之间的空间中，电位函数遵循泊松方程（5.0.2)式。在规定的体积√中，这个方程的特解可由重叠积分(4.5.3)式给出。p(r')dy0,(r)=j,.4xelr=r)(1)在体积V中各点工，这一电位避循泊松方程。由于我们1并不计算此方程在体积V外的值，式(1)

中要求的对源的积分，只需要包含体积√中的源。这就使得特解并不是唯一的这点很清楚，因为由体积V外任意电荷的积分造成的对电位的增添，只能引起一个在体积V中其拉普拉新导数为零的电位。式(1)是完整的解吗?因为它不是唯一解，所以答案当然应该是不。进一步说，跆解中并不包含有关导体的位置和形状这些信息是很清楚的。因此，一般来说，作为式(1)电位Φ，的负梯度所求得的电场，在电极表面具有有限的切向分量。另一方面，导体具有面电荷分布，它能自行调整使得产生在导体表面的净电场具有零值的切间电场分最。这些面电荷的分布最初并不知道，因此不可能包括在式(1)的积分中。走出这一困境的方法是：在这个空间中没有导体处，我们寻求的电位分布足两种电荷分布的结果。第一种是导致电位函数Φ，的给定的体电荷分布，第二种足分布在导体表面的电荷。由面电荷产生的电位函数在所关心的空间√中必须遵循无源的泊松方程。我们用电位函数Φ来表示齐次形式的泊松方程的这个解。那么，在体积V中，Φ。必须满足拉普拉斯方程。Vbn=0(2)根据叠加原理，总电位可写成Φ=0,+0(3)现在，求完整的电场分布的问题已简化成寻求一-个使式(8）的净电位在表面：上具有给定的电位：的解答问题。现在Φ，为已知的，并可在表面S，上求出其值。于是对S；计算式(3)的值，给出(0)=Φ,(S) +@n(S)因此，在边界S，上，现定齐次解答为@n(S) =V-Φ,(S)(6)所以，对于给定了边界上电位情况下的电准静态场的确定已简化为求满足由式(5)给出的边界条件的拉普拉斯方程式(2)的解问题。本节形成的方法是能应用于第4章最后部分中边值问题的另一观点。当然，图5.1.1提低的边值情况的抽象图形与图4.6.1的图形并无不同之处。在例4.6.4中，图4.6.8所示的电场是对于位于不带电的等电位球面电极附近的一个点电荷所确定的。在电极外所讨论的体积V中,体电荷分布是奇异的,即点电荷9。实际上,由式(4. 6.35)给出的电位，是式(3)的形式。特解可以看作是第一项，即点电荷的电位。而第二和第三项，等效于球体中两个虚设的也荷引起的电位，可看作是齐次解。为满足边界条件的叠加方法在以下几节中，将经常利用叠加作为满足边界条件的另一种方式。假设在体积V中没有电荷密度，非且在n个表面上每一个S，上的电位分别仍是。丁是@-0(6)Φ=u在S,上，j=1,n(7)解咨被分解为中，的叠加，Φ，是第3个表面上满足所要录的条件而点新有头地上为零的.112

一个解。0-2.(8)在S，@,=fo(9)在S...S.-.$S+.S.每一项都是拉普拉斯方程式(6)的一个解，所以它们的总和也是拉普拉斯方程的解(10)70,=0在5.5节中，提出了在包围所讨论的体积的四个表面中任何一个表面上满足任意边界条件的一种方法。电容矩阵假设在n个电极系统中，要求得第i个电极上的净电荷。根据式(8)，E·da在包围这个电极的表面S，上的积分为I-f evo.da=-fevo.da(11)由于拉普拉斯方程的线性性质，电位Φ，正比于激发这一电位的电压。由此得知，式(11)可写成独立于激励的电容参数的形式。即式(11)变为2-20u:(12)11其中电容系数是-$eovo,da(13)在第；个电极上的电荷是所有n个电压所作贡献的线性叠加。与自身电压相乘的系数C称为自电容，而其他的系数Cu,i3，都是互电容。5.2泊松方程解的唯一性在这一节中，我们将说明服从泊松方程的一种电位分布，如果在界定体积的表面上电位是确定的，那么在体积V中也是完全确定的。这样-个唯性定理所以是有用的，有两个原因：a)它说明如果我们已求出泊松方程的一个解。不论是通过数学分析还是物理理解，那么我们就求得了这唯一解；(b)它说明了什么边界条件适合于唯一地确定一个解。如在所讨论的区域中没有电荷存在，那么这一定理就陈述了拉普拉斯方程解的唯一性。根据“归谬法”，我们假设解不是唯一的，即存在两个解，Φ。和Φ，它们满足同一边界条件，然后我们来证明这是不可能的。我们推测的两个不同解Φ，和Φ，必须满足具有同一电荷分布的泊松方程，同时必须满足同一边界条件·113

(1)v0..-;@=在s上(2) V?0,=P焦上由此可将中定义为两电位之差值，，=()=0;0在上(3)现在一个很简单的论据证明Φ。既能满足拉界定V的表面S普拉斯方程又在所有边界面上为零的唯一方式是等于零。首先，论证@。在V内部任何一点上不可Vo的线能具有最大或最小位。借助于图5. 2.1，设想。梯度的负值为通过某一点r，的场线。因为电场是无散的(散度为零)，这样一根场线不能在V中发出或终止（参考2.7节）。进一步说，电场规定了图 5.2.1起始于边界面的某一部分经过点后终止于边界面的另一部分的电场线。一个电位(4.1.4)式。因此，当顺着负梯度方向沿着场线运动时，电位必须减小直到场线到达界定√的表面S，中之一时为止。类似地，当沿相反方向运动时，电位必须增加,直到到达边界表面中的另一个。因此,所有Φa(r)的最大和最小值必须位于表面上。在任何一个内点上的差值电位不可能设想比边界表面上电位的最大或最小值更大或更小。但边界表面本身处于零电位。由此可知，在V中差值电位到处为零，即=Φ。因此，对于用式(1)陈述的边值问题存在唯一的一个解。5.3连续性条件在金属导体的表面，电荷密度积聚在仅有几个原子间距的厚度中。在描述它们的电场时，对于在这个薄层内部电场分布的详细情况通常并不关心。于是，电荷用面电荷密度式(1.3.11)表示，并且把承载电荷的表面当作不连续的面来处理。在这样情况下，为了方便，常把要确定电场的体积分割成几个被这些不连续表面分陷开的区域，并用分片连续的函数表示这些电场。因此，就需要用连续性条件来联系由不连续表面分隔开的两个区域中电场的解。 这些条件包含在适用于整个区域的微分方程中。 它们确保电场甚至在通过不连续处都符合基本定律。四个麦克斯韦方程中的每一个都隐含了一个连续性条件。由于源的分布的奇异性，可用达些定律的积分形式将不连续表面两边的电场联系起来。如果定义失量n为不连续表面的单位法线,且由区域(b)指向区域(a),这些连续性条件汇总在表1. 8. 3 中。在 EQS 的近似法中,最重要的定律是没有电磁感应的法拉弟定律和高斯定律，即第 4章的前两个方程。因此，相应的EQS的连续性条件是nx|E-E}-0(1).114 :

n.(E*-eEb) -0.(2)因为在任何情况下，电磁感应对法拉第连续性条件都没有影响，所以这些条件与一般电动力学定律中的条件是相同的。作为提示，包围着法拉第定律在其上进行积分(1.6节)以求得式(1)的积分表面的周线，示于图5.3.1a中。根据高斯定律（1.3节）以求得式(2)所用的积分体积同样示于图5.3.1b中。图5.3.1（a）与承载面电荷密度的表面相交的微分周线。（b）包围在法线为n表面上面电荷的微分体积。电位的连续性条件是什么呢？横跨过一个不连续的面，即使在那个面上带有面电荷密度的情况下，电位中也是连续的。当场强E是有限时（包含一个无穷大的电场的偶极子层会引起电位的跃变）将是这样一种情况，因为，那时路径长度为无穷小，电场从表面一边到另一边的线积分为零。p*@h=0(3)为了确定描述高斯定律通过不连续面的跳跃条件，我们对图5.3.1b所示的与不连续面相交的休积进行了积分(1. 3 节)。对所得到的连续性条件式(2)，考虑到在 EQS 的近似法中 E=一的关系，写成用电位表示的形式(4)n[(vd)*-(vo)"]=--T在带有面电荷密度的突变面上，电位的法向导数是不连续的。如果连续性条件用来描述在体积中成立的那些定律所隐含的条件之外的物理约束，它就成为边界条件。一个熟悉的例子是电位受约束的电极表面处。因此，连续性条件、式(3),要求在邻近于电极的体积中的电位应该是给定的电极电位。如果没有援引在体积分形式的定律中不表示的关于电极的物理特性的信息（例如，它们是“无限导电的")，就不能证明这-一陈述是正确的，因此，也就不是连续性条件所固有的。5.4笛卡儿坐标系中拉普拉斯方程的解我们已经研究了泊松方程解的一些普遍特性，现在来讨论受边界条件约束的拉普拉斯方程求解的特殊方法是拾当的。这节和下一节将举例说明在描述EQS场时经常采用的三个标准步骤。首先，在边界面就是坐标面的坐标系统中建立拉普拉斯方程。然后，把偏微分方程通过变量分离化简为一组常微分方程。用这一方法产生了无数组的解。最后，通过附加上由变量分离·115

所求出的留使边界条件得以满足。在本节中，如果规定的边界条件是沿着某一笛卡儿然标系的坐标面，那么求出的为自然解。假设电场仪与二维坐标和9有关，那么拉普拉斯方程是（表I)30+=0一种历史悠久的数学方法是将这一个新问题简化这是一个具有两个自变量的偏微分方程。成一个以前解决了的问题，这里求解偏微分方程的过程就简化为对常微分方程求解的过程。这是用分离变量法完成的。它由具有特定的对空间依从关系的慢设解所组成。D(r,) =X(r)Y(y)(2)在式(2)中，假设X只是的函数,Y只是？的函数。如果需要的话，那么一个普追的空间依赖关系可通过这些特殊解的叠加而重新恢复。把式(2)代人式(1),并除以Φ给出dex(a)Y(u)(3)X(a)drY(u)d这里用了全导数符号是因为函数和根据定义分别只是和的函数。现在，在式(8)中左边只有的函数,而右边只有?的函数。只有当每个表达式都为常数时，方程与α和无关的条件才能够满足。我们用定义这个“分离”常数，由此可得-x(4)和-y(5)这些方程的解为X~coskr(6)或sinka(7)Y-coshhy或sinhhy如果=0,这些解答就简化为(8)X~常数或2Y~常数(9)或乘积解即式(2)，汇总在表5.4.1的前4行中。花右边一列中的解只是将中间一列的解的？表5.4.1拉善拉斯方操的二维笛卡儿解h0k=0"<0(→j8)带数coskreoshkycoshl'acosk'ycoskasinhkyr,Rsinrahisinka sinhtysinht'wsink'y'seocoshre*"e-*cost'yinkset:er'ssink'gye-vrsink'ssinkze-:116

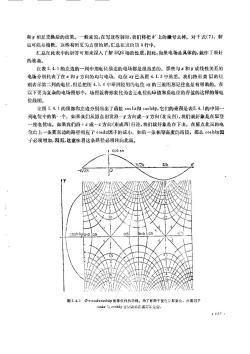
和y相互交换后的结果。一般来说，在写这些解时，我们将把上的撤号去掉。对于式（7），解也可能是指数。这些有时更为方便的解，汇总在表的后4行中。汇总在此表中的解答可用来深入了解EQS场的性质，因此，如果电场是具体的，就作了很好的准备。在表5.4.1的左边的一列中用电位描述的电场都是很熟悉的。那些与和?成线性关系的电场分别代表了在和g方向的均匀电场。电位已从图4.1.3中熟悉。我们将用类似的规则表示第二列的电位，但是把图4.1.4巾举例说明的电位3的三维图形记住也是有帮助的。在以下更为复杂的电场图形中，场图就将形象化为含正电位的峰值和负电位的谷值的这样的等电位线图。在图5.4.1的顶部和左边分别画出了函数coska和coshng，它们的乘积是表5.4.1的中间一例电位中的第-·个。如果我们从原点出发沿十方向或一！方向（北或南），我们就好象是在攀登一座电位山。如果我们沿十或一方向（东或西）行避，我们就好象是在下山。在原点北面的电位山上一条更东边的路径相应于coska因子的减小。如沿一条相等高度的路径，那么coshy因子必须增加，因而，这意味着这条路径必须转向北面。OS图5.4.1@等位线和场，分离因子无先边oskrtenshk分周装示在！117

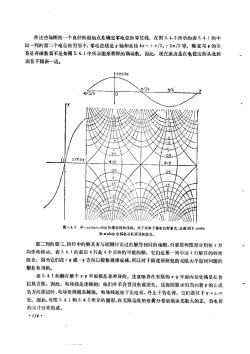
作这些场图的一个良好的起始点是确定零电位的等位线。在图5.4.2所示的表5.4.1的中间一列的第二个电位的图形中，零电位线是轴和直线zz=+元/2，+3元/2等。现在与3的关系是奇函数而不是如图5.4.1中所示图形那样的偶函数。因此，现在原点是在电位山的从北到南往下倾斜一边。b13.摩位线和场线。为了有助于使电位形象离因子cos和inh分码表示在顶部和左第二列的第三，四行中的解具有与刚刚讨论过的解答相同的场图，只要那些图形分别在方向作些移动。 表 5. . 1 的最后 4 行是 4 个另外的可能的解，它们是那一列中前 4 行解答的线性组合。因为它们在十或一方向以指数规律衰减，所以对于描述所研究的无限大半空间问题的解是有用的。表5.4.1的解在整个2-平面都是非奇异的。这意味着在有限的-平面内处处满足拉拉斯方程，因此，电场线是连续的；他们并不会置出来或消失。这些图显示出当向着！的正或，负方向推进时，电场变得越来越强。电场线起始于正电荷，终止于负电荷，它们都位于3→±。处。因此，对图5.4.1和 5.4.2 所示的图形,在无限远处的电荷分布必须由无限大的正、负电荷的交替分布组成。118 :

最后两段话用作进一步扩大对拉普拉斯方程解的性质的了解。肯先，第三维可用于以图4.1.4的方法来表示电位，使得电位表面具有从边界铺设的一张薄膜的形状，薄膜的高度正比于它们的电位。拉普拉斯方程式（1）要求反映在和3方向曲率的量的总和为零。如果一个函数的二阶导数为正，它就向上弯曲；如为负，就向下弯曲。如果曲率在方狗为正，那么在方向必为负。于是，在图5.4.1中的原点，电位在“方向的偏移是向下成凹形，所以在多方向，电位的偏移一定是向上成凹形的。类似的挂断必然适用于-平面上任一点。其次，因为出现在表5.4.1的第二列的周期函数中的与在指数函数和双曲线函数中的相问，很明显，周期的变化越快，衰减或外观的增长也越快。5.5满足边界条件的模态展开式上一节中用分离变盘法得到的每一个解可以由作用在=常数和一常数的平面内一对平行的表面上的适当的电位来产生。例如，考虑表5.4.1的≥0列中带有恒定乘数的第四个解为D-Asinkrsinhhy(1)这个解在=0的平面和a=n/的平面中，@=0，其中n是一个整数。假设我们令k=nt/a,使得在y=a平面中@也等于零。那么在g=b平面，式(1)的电位P(a,b)=Asinhnbsinn(2)具有对的正弦关系。如果式(2)形式的电位沿着在=b表面作用，并且在=0,x=a和9=0面上保持零电位（警如说，通过保持零电位的平面导体），那么，式(1)的电位将在0<<a，0<<b的空间内部存在。每一段电极受适当电位约束的许多分段电极可以用作9=b处电位的近似分布。图 5. 5. 1 中给出了 n=1和 n=2 时的电位和电场图。注意到 5. 2节中的定理保证所确定的电位是唯一的。d-yaoX=0Xsa-a处中=0图5.5.2在预部插入一电位为的电图5.6.1可以满足边界条件在9=0和-0,2的其有式(1)形式的无数个电位函数中的两个。极的零电位矩形情的积截面。119