《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第7章 传导与电准静态的电荷弛豫

第7章传导与电准静态的电荷弛豫7.0 引言本章是主要与静电场和电准静态场有关的儿章中的最后一章。电场E仍旧是无旋的，所以能够用电位@表示。xE=0E--V0(1)E的源是电荷密度。在第4章中，我们把这个源的分布看作是规定的来开始我们对EQS场的研究。到第4章结束前，我们确定边值问题的解，在那里等位面用完纯导电金属电极代替。在那里，以及在整个第5章中,象面电荷密度一样存在于电极表面上的源与场自相一致。然而在体积内，电荷密度仍是规定的。在第6章中，两步中的第一步是对体积中的电荷密度作出自相一致的描述。在通过高斯定律使E与它的源相联系时，我们认识到存在两类电荷密度，p 和 P，它们分别表示不成对的和成对的电荷。成对的电荷与极化强度P有关，结果商斯定律可以写成式(6.2.15)V·D=p?式中D三E.EP。在第6章中，一直假定体积是完全绝缘的。这样，P，或者为零，或者是给定的分布。对于体电荷密度自相一致的描述的第二步，把表示不成对电荷守恒的方程(2.3.3)式J+e=0(3)加到式(1)和(2)。出现在此方程中的电荷确实是不成对的电荷密度，通过对有极化时的安培定律式(6.2.17)，取散度，并利用式(2)给出的高斯定律消去D得出。要利用这三个微分定律，必须规定P和J。在第6章中，我们知道前者通常由规定极化强度P或通过引人P和E间关系的极化构成定律来完成。在本章中，我们将几乎总是涉及线件电介质，那里D=eE。需要一个联系J。和电场强度的新的构成定律。因此后面诺节中的第一节致力于传导的构成定律。当7.1节结束时，在我们而前有微分定律,它们是本章的主题。在进行下面的推导之前，与电路理论作一类比是有帮助的。如果前两章被认为是描述含有相互联接的电容器的电路，如图7.0.1a所示，则本章在电路中添加上电阻器，如图7.0.1b那样。假设电压源是阶跃函数。当电路由电阻器和电容器组成时，电路中也流和电压的分布最终只189

图7.0.1电位和电流密度的EQS分布类似于电阻器和电容器网络中的电压和电流分布。（a）完纯电介质和完统导体系统类似于电容网络。(b)本章中考虑的传导效应类似于在网络中乘加电阻器所引入的效应。由电阻器确定。这就是说，当t->o时，电容器停止充电，并且等效于开路。于是电压的分布曲通过电阻器的稳定电流确定。在这一长时间的极限情况下，电容器上的电荷决定于已经根据电阻网络确定的电压，稳定出流类似于在电荷守恒表达式(3)中apa/at-0时场的情况。我们将会发现,(1)和(3)两式，当后者用由传导构成定律表示的J，写出，就完全确定电位和E的分布，从而也确定J的分布。正如图 7.0.1b 的电路中,电容器上的电荷用已经确定的电压分布表示一样，电荷分布可以用高斯定律式(2)，从已经确定的场的分布，以求后的方式求得。在7.1节中考虑了一般传导构成定律的物理基础之后,7.2—7.6诸节专门用丁稳定的传导现象。在图7.0.1b的电路中，在阶跃电压施加后的--瞬间的电压分布由电容器决定，而与电阻器无关。 根据场论的观点,这是第 4 和 5 章中所描述的物理情况。 7.7一7. 9 诸节的目的是建立起对于这场与源的初始分布怎样驰豫到已在7.2—7.6 诸节中研究过，当t→>20时占优势的稳定条件的理解。在第3一5诸章中，对于导体，我们引用了“完纯电导率”模型。对于电准静态系统，我们将以对于“在什么情况下导体可以被看成是完纯的？"问题的回答，作为本章的结束。最后，如果场和电流基本上是静态的,则 EQS 和IMQS 的定律之间没有差别。这就是说，如果在MQS系统中2B/at是可以忽略的，法拉第定律仍简化为式(1)。因此，本章的前半部分不仅对EQS系统，而且也对一一些MQS系统中的稳定传导提供理解。在第8章中，我们从给定的电流密度分布确定磁场强度。假如变化率足够慢，使得电磁感应的影响可以忽略，在7.2-7.6诸节中所论述的稳定传导问题的解为开始讨论第8章提供了所需要的磁场源即电流密度的分布。究竞场能变化多快而不致产生电磁感应的影响？对于EQS系统，这个问题的回答出现在7.7-7.9诸节中，有限电导率和有限变化率的EQS 影响与它们在MQS中的对应量形成尖锐的对比，后者将在第10 章的后半部分研究。7.1传导构成定律存在物质时，场在空间变化至少在两个长度尺度范围内。微观尺度典型地是原子之间或分子之间的距离,而大得多的宏观尺度典型地是由材料构成的物体的尺寸。正如前一章所阐述的，极化媒质中的场是偶极子的微观尺度上的平均值。 实际上，实验确定的使宏观的 P 和 E 联系: 199

的极化构成定律(6.4节)，并不涉及微观场。在实验测得的值仍将用来计算宏观参数的条件下，我们假定在物质内部作用于不成对电荷或口由电荷上的平均力与洛仑兹力即式(1.1.1)有相同的形式。f=g(E+V×μH)(1)与极化电荷相反，自由电荷不是被约束在构成物质的原子或分子上，但在电场和磁场的影下，它能通过的距离比原子间或分子间的距离要大。通常，带电粒子与原子或分子的组成物相碰，因此由式(1)给出的力并不会像对在自出空间中的带电粒子那样导致均勾的加速度。事实上，在一般的传导过程中,粒子在所关心的时间范围内要经受那么多次的碰撞，使得它获得的平均速度相当低。这一现象产生两个结果。第，在时间平均值内，作用于粒子工力的平衡可以忽略惯性的作用。第二,速度太低使得磁场引起的力通常可以忽略。（磁力项导致霍尔效应，在金属导体中它很小并很难观察到，但是在半导体中由于电荷载流子达到的相对较大的平移速度，比较容易观察到。)在认为驱动力完全是由电场引起的，非且使它与正比于带电粒子的平均平移速度的“粘滞”力平衡的情况下，力方程变成(2)f--±l4lE=y+式中上面和下面的符号分别对应于正和负心荷的粒子。系数是正的常数，它表示由载流于与固定的原子或分子的碰撞引起的时间平均“阻力”，载流了是通过原子或分子而移动的。用迁移率 μ+表示,根据式(2),可把正和负粒子的速度写成(3)V=μE式中μ±=1±1/±。迁移率规定为正的。正和负粒子分别沿着或逆着电场强度而移动。现在假定有两类带电粒子，一类是正的而另一类是负的。它们可能是当盐溶解在水中时产生的正的钠离子和负的氯离子。在金属中，E电荷表示(零迁移率的)原子的空穴，而负的粒子是电子。于是，当N。和N-分别规定为每单位体积内这些带电粒子的数目时，则电流密度为(4)J.=N+19+lV+-N-19-1v负粒子通量构成的电流的方向与粒子运动的方向相反。囚此式（4）中的第二项有负号出现。此表达式中的速度通过式(3)与E相联系，所以得出也流密度为(5)Ja-(N+19+Iμ++N-Ig-Iμ-)E用同样的变量表示，不成对的电荷密度为(6)Pu=N+1Q+/N-19-1欧婚传寻通常，粒子密度N。和N-的分布由电场确定。不过，在许多材料中，式(5)括号中的量是材料的性质，称为电导率0。(7)[J=GE;O=(N.19iμ.IN-I9-Iu-)的MKS单位是(0一m）云西门子/米=S/m。+191

在这些材料中，电荷密度N，9.和N-9-保持相互（近似)平衡，所以外施场对于它们的和儿乎没有作用。这样,电导率α(r)在非均匀媒质中规定为位置的函数，用材料中的 N+分布和局部迁移率表示，它们也可以是的函数。式(7)给出的传导构成定律是欧姆定律在场理论的意义上的推广。一些常见材料的电导率的值在表 7.1.1中给出。记住任何构成定律的应用都是有限制的，欧姆定律也不例外，这是重要的。对于金属和半导体，在充分大的尺度上，它通常是好的模型。它也被广泛用于处理电解质。但是，当材料变成半绝缘体时，它的有效性就成问题。表 7.1. 1 各种材料的电导率固体状态的金风和合金α-S,m,200时铝，工业用冷拔3.54X10m期，退大的5.80X(0%钢，冷拉5.65×107金，完全延伸的4.15X107饮,99.98%1.0X10钢粉0.5-1.0 ×100.48X109中2.17×10%锦络合金0.10×107缘1.28×10根，99.98%6.14X1071.81X107半绝终和电介质固！酚醛塑料(平均值范围)*10-8-10-1赛璐珞*10*玻璃,普通的*10~12硬橡皮*10-14-:0-10云胜*10-110-15石蜡10-14-44-1石英，格凝的*小于.0硫*小0聚四张乙烯小于10-水银0.1X107酒糖，15°℃3.3X10-*蒸馏水，1802X10-*玉米淇5X10-*对于离度绝绿的格料，缺娘定律的行效性是可怀疑的，电导率的值只在估算时有用。192

单向传导要建立对欧姆定律本质的了解，把它与单向传导的定律对比是有用的。在后一种情况下，只有一种符号的带电粒子在中性的背景中运动，因此代替(5)和(6)两式的电流密度和电荷密度的表达式为(8)J.=loluE(9)式中电荷密度p现在带有它自己的符号。用这些关系描述的典型情况是离子通过空气的迁移。要注意只是在有净电荷密度的时候，在单向传导中才存在电流密度。相反地，对子欧姆传导,电流密度和电荷密度分别由(7)和(6)两式给出，在没有净电荷密度的地方可以有电流密度。例如,在金属中,带负电的电子通过固定的带正电原子的背景运动。这样,在(7)式中 μ+-而电导率完全起因于电子。但由（6)得出，正电荷确有重要的作用，在那里它们可以使电子的电荷密度等于零。我们常常会发现在欧姆导体中，在没有净的不成对电荷密度的地方，有电流密度。7.2稳定的欧姆传导为下两节作准备，考虑有线性极化率并用欧姆定律式(7.1.7)描述的材料中的场。J=g(r)E; D=e(r)E(1)通带，这些特性是位置「的函数。典型地，电极用来约束包围此材料的一些表面上的电位，如图7.2.1所示。在本节中，我们假定在任何给定的位置，电荷积聚的速率对电流密度的分布的影响可以忽略不计，在此意义上，激励基本上不随时间而变。这样，在电荷守恒定律式(7.0.3)中，不成对的电荷密度的时间导数可忽略。这意味着电流密度是无散的。(2)图7.2.1 由面8*和8*所包围的体积的图形。8上VE-0的电位是受约束的，而8*上电位的法当然，在 EQS近似中，电场也是无旋的。向导数是受约束的。(3)VXE-0>E=-将(2)和(3)式结合，得出电位分布的二阶微分方程(4)V.0V-0在均勾电导率（α二常数)区域中，它呈现熟恶的形式。(5)0=0·193

在均勾导体中，电位分布满足拉普拉斯方程。在均勾导体中，电位分布获得拉普拉斯方程的物理原因，与第4和5章中电准静态情况下导致拉普拉斯方程的物理原因是十分不间的,认识到这一点是重要的。当稳定传导时,决定性的要求是电流密度的散度为零。不成对的电荷密度并不影响电流分布，而是由它确定。在均勾导体中，连续性对了的约束碰巧意味着没有不成对的电荷密度。在不均勾导体中，式(4)表明有不成对电荷的积聚。确实，当α是位置的函数时，式(2)成为(6)V·E+E.V0=0一经求得电位分布，就可用高斯定律来确定不成对电荷密度的分布。(7)Pu=EV.E+E.ve方程(6)可以用来解出divE,然后将该量代人式(7),得到P=-E-Va+E-Ve(8)即使的分布在确定E时不起作用，但通过高斯定律，它却影响了不成对电荷密度的分布。连续性条件在电导率突然变化处,从式(2)和(3)可得出连续性条件。从式(2)导出的条件(9)n.(o,E*-o,Eb) =0正如从高斯定律得到的式(1.3.17）一样。由式(3)包含的连续性条件已在5.3节中熟悉。n×(E*-E)=00.-0=0(10)图例说明绝缘表面处的边界条件绝缘的导线和普通的电肌器是导电媒质被基本上是绝缘的媒质界定的例子。应该用什么边界条件来确导电材料内部的电流分布在图7.2.2中，区域(a)与区城(b)相比是相对绝缘的，0,《αb。由式(9)得出区域(a)中的法向电场比区域(b)中的大得多，》。根据式(10)，E的切线分量是相等的，一。假定在绝缘区域内E的法向和切线分最的大小有相同的数量级的情况下,这两个语句分别建立了E的法向和切线分量的相对大小,示于图 7. 2. 2。 我们)可以断定在相对导电的区域(b)内，E的法向分量与切线分量相比基本上为零。因此，要在相对导电区域内确定场，在绝缘表面处使用的边界条件是(11)nJ=0->n.y@=0+ 194

在绝缘边界处，在导体内，电位的法向导数为零，而边界的电位调节它自身使这成为事实。电流线转变方狗使得它们保持与绝缘边界相切，如图7.2.2所示。正如包含在式(8)中的高斯定律在事后用来求出不成对的体电荷密度一样，高斯连续性条件式(6.5.3)，可用来计算不成对的面电荷密度。与电流连续性条件式(9),结合在一起，它成为 (-)(12)电如果只有两个电极连接图7.2.1中的导体，从而只有一个电压=和一个电流=端口的电压-电流关系有如下的形式(13)G式中G为电导。为了使G与场量相联系，把式（2)对面S所包断的体积V进行积分，并且用高斯定理将体积分转换为电流gE·da对面 S的积分。于是此积分定律应用于图 7. 2. 1中所示的包围连接到正端钮的电极的表面。在那里它横切导线，贡献是一i，以致对闭合面的积分变成oE.da=0(14)式中S，是电位为的完纯导电电极与欧姆导体的界面。将式(14)除以端电压就得出由式(13)定义的电导的表达式。oE-da(15)注意决定电位分布的方程式(4)的线性性质保证i正比于。从而式(15)与无关，并且确实是表征与激励无关的系统的一个参数。对电导的式(15)与对电容的(6.5.6)式的比较，启示一种模拟，这将在7.6节中计论。导体中场的定性图素图7.2.3中说明三类稳定传导形式的特征。在第一类中，所关心的区域是一个有均勾电导率，被具有受约束电位的表面或被完纯绝缘体所界定。在第二类中，在界面处电导率有突变，但11.1148884F图7.2.3包含导电材料和完维导电电极的典型形式。(a)所关心的区城充满具有均匀电导率的材料。(b)由不同的有均勾电导率的材料构成的区域。在界面处电导率不连续。(c)电导率卡滑地变化。195

数量是有限的，而在第三类中，电导率是平滑地变化的。因为高斯定律在确定电位分布时不起作用,在这三类形式中介电常数的分布是任意的。当然,它们对于所引起的不成对电荷密度的分布有强烈影响。在导体内电场分布的定性图景是根据类似于6.5节对线性电介质所用的论证形成的。因为J是无做的，并与E有相同的方向，它通过管子从高电位电极到低电位电极，这些管子内的J线既不终止又不起始。E线形成同样的管子,但或者终止或者起始于不成对电荷与极化电荷的和。这些电荷密度的和是dive-E,它可以由式(6)确定。- E0J.2gP+P,-VE--E..(16)在突然的不连续处,面电荷密度的和确定 E的法向不连续性。考虑到式(9),O.+o,=n.(cE*-.E)=nE(1-g)(17)注意e的分布在使E线成形时不起作用。在图 7.2.3a的均匀导体中，从高电位沿着典型的电流管到低电位时，没有碰到电导率梯度，所以式(6)告诉我们不存在E的源。从而，在整个均勾导体中@满足拉普拉斯方程是不奇怪的在沿着电流管通过图7.2.3b的不连续处时，从低电导率到高电导率，式(17)表明存在E的负值而电荷源。因此,E趋向于从较导电的区域中被排除而在导电较差的区域中塔加。当电导率在如图 7. 2. 3 ℃ 所示 E 的方向平滑地增加时，E-Vo 是正的。 因此，E 的源是负的，而E线沿着通量管减少通常碰到的是均勾和分块均勾的导体，这一类的例子将在7.4和7.5两节中讨论。电导率是平滑地分布的例子类似于6.7 节中示例的平滑地变化的介电常数的情况。在简单的一维构型中，下面的例子说明所有三种类型。例 7.2.1、一维电阻器图 7. 2. 4 所示的电阻器在任何 2一多平面有相同的截面积 4。 沿它的长度4 有电导率 α(1)。完纯导电电极把0处的电位约束为，处的电位约束为零。圆柱形导体被完纯绝缘体包国。馥定电位只和1有关。因此,电场和电流密度是1方向的，并且,没有垂直于绝练边界E的分盘这一条件是自动斑满足的。对于一维场,式(4)简化为(od)0(18)括号中的量即电流密度的负值,在电阻器的整个长度上是不变的。 这样,当小。定义为需数时，ode--.(19)现在将这个表达式从下南的电极到任意位置积分darsTedy(20)02-500在多一比和Φ一处计算这个表达式，就使电流密度与端电压相联系。-J.e./1o(21)· 196

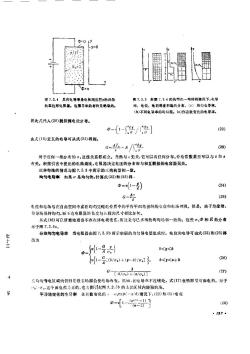
围 7. 2. 4 具有电导率是电极间位经势的两数图 7. 2. 5 在围 7.2. 4 的移型的一些转殊情况下,电导率、电位、电荷密度和场的分布。（a）均幻电导率。的圆柱形电阻骤。包圖导体的材料是绝缘的。(b）不同电导本的均勾层。（c)作指数变化的电导将此式代人(20)就得到电位分布。[1-{% /%](22)由式(15)定义的电导可从式(21)得到G-Afes/'dy(23)对于任何一维分布的0，这些关系都成立。当然与无关，它可以有任何分布。介电常数甚至可以与和z有关。根据引言中提出的电路类比，电阻器决定电压的分布而与相互联接的电容器无关。三种特殊的情况与图7.2.3中所示的三类构型相一致。均匀电导率 如果α 是均勾的,计算式(22)和(23)得,(24)$=e(1-)G-Ao(25)电位和电场与在自由空间中或在均匀究纯电介质中的平行平面电极问的电位和电场相同。但是，由于绝缘璧，传导场保持均匀,而不论电阻器的长度与其核向尺寸相比如何。从式(16)可以清慈地看出不存在体电荷密度，而这是与已崇得的均勾场相一致的。这些6,Φ和E的分布亲于图 7. 2. 5a分块均匀电导率当电阻器由图7.2.5b所示串联的均勾导电层纽减时，电位和电导可由式(22)和(23)得t出为Jl-%?0<<b5(26)(0f1-%:(0/0)+(9-6)/0.1 /b<<a+b(27)[.b/0)-(a/)]在均勺导电区域内仍归是设有场源会使电场改变。然猫，在电导离不连续处，式(17)表明那里有面电荷。对于0，这个面电荷是正的，它力图引起图7.2.5b的L部区毅内较强的场。平滑地变化的电号率在指数变化的4,exp（—3:d)情况下，(22)和(23)变成@-[1--(e-1)(28)197

(29)a(a)这里叫起E的分布的电荷密度由式（16）因此，电场从下部区域被作指数增加的体电荷密度所屏崴7.3分布的电流源和相关的场在稳定条件下，电荷守恒要求电流密度是无散的。因此，J线无始无终。迄今我们认为电流管是起始于所关心的区域的外部,即在边界上。有时引入规定为s(r，t)A/m的体分布的电流源是方便的，从而稳定的电荷守恒方程变成(1)f, J.da=f,sdvvJ=s当我们现作定义了奇异源并考虑它们怎样能够物理地实现时，引人分布的电流源的动机就变得清楚了。分布电流源的奇异性式(1)和高斯定律之间的相似性要求点，线和面电流源的定义如图7.3.1所描述。回到1.3节，那里规定了类似的奇异电荷分布时，应该记住我们现在考虑的是电流密度源，不是电通量源。点电流源引起流出体积的净电流，此体积收缩到零，然而始终包围着源。(e))()图7.3.1上面一行概念性地表示奇异的电流源分布，下面一行提出它们如何可以通过绝缘导线馈电的电极物理地实现f,Jda=i, i,= lm Jsdo(2)im100- 198