《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第4章 电准静态场 重叠积分观点

第4章电准静态场：重叠积分观点4.0引言首先从研究电准静态场开始的原因是因为这种矢量场的表示比较容易。法拉第定律的电准静态形式要求电场强度E是无旋的。VxE=0(1)电场强度是通过高斯定律与电荷密度β相关的。(2)V.e.E-p这样，电准静态场的源是一个标量电荷密度P，而在自由空间中，磁准静态场的源是个尖量电流密度，标量源比矢量源简单，这就是我们为什么首先从电准静态场着手的原因。本章的大部分是关于给定了β的分布，根据这些定律找出E的分布。但在本章结束之前我们将寻求被导体界定的有限区城中的电场。在许多实际的场合，只有在电场已经确定后，边界表面上的电荷分布才能知道。因此，本章为在第5章中解决边值问题作了准备。我们从建立电位开始，作为可唯一地描述无旋的电场强度的标量函数。梯度算子和梯度定理是推导的产品。然后，综合式(1)和(2)可得到泊松方程的标量形式。这个方程将被证期是线性的，由此得出，由电荷叠加产生的电场是有关的个别电荷所产生的电场的叠加。所得到的重叠积分说明了电位，因而也说明了电场强度如何由给定的电荷分布来确定。因此，在4.5节的最后，我们得到了求解式(1)和(2)的一般方法。在一个限定的区域中，如何确定电荷分布，使由此得到的电场满足边界条件的方法，将在4.6和4.7节中举例说明，最后，用重登积分法求解边值问题的更为一般的技巧，将在4.8节详细说明。对于那些对电路理论有一定基础的人来说，如果能意识到这一章和下一章使用的方法是早已熟悉的，将是有益的。在三维空间求式(1)和(2)的解，就象求解电路方程一样，只是电路中只有一维的时间，在电场问题中，电荷密度是激励函数。求出电路响应的一种方法是基于先求出对于一-个冲击的响应。然后，对任意激励的响应可由该激励源分解出来的各冲击响应的叠加来确定。这个响应采取了重尧积分的形式——卷积积分。作为我们研究的起点，泊松方程的冲击响应是一个点电荷的电场。因此,本章的主题是求解方程(1)和(2)的卷积方法。在下一章的边值方法中，还会利用我们熟悉的也路理论的概念。一个解由两个部分组成：由激励源产生的特解和满足边界条件所要求的齐次解。将会发现重登积分是找出特解的一种68

方法。4.1用标盘电位表示的无旋电场：梯度算子和梯度积分定理-个无旋电场从某一个参考点rrer到位r的积分是与它的积分路径无关的。这个结论是从式(1)对S面的积分得到的，如图4.1.1所示，S面由可选择的路径I和I限定的边界线所包围。斯托克斯定理(2.5. 4)式给出了Eds=0I.VxE.da=(1)斯托克斯定理用的是围绕S表面单一方向的周线的线积分，而电场从r到rrat，即从点a到b 的两个线积分是以相反方向沿周线进行的。考虑到路径增量的方向，式(1)等价于f.E.ds-f..E-dsE.ds'-0(2)A腔因此，对一个无旋场来说，两点闻的电动势与路径无关E.ds-fwE.ds'(3)如果一个场，它在两点间的线积分是与路径无关的唯一值，称为“守恒场”。如把参考点保持固定，则线积分就是积分终点r的标量函数。我们用符号Φ(r)定义这个标量函数(r"E.ds@(r) -@(rrer)= /(4)并且称Φ(n)为点「相对于参考点的电位。假如各终点组成了可以连接导线的“节点"，式(4)的电位差就是点相对于参考点的电压。典型地，后者是“地"电位。因此，对于一个无旋场，1.6节中定义的电动势就变成a点相对于b点的电压我们要说明标量函数 Φ(r)与电场 E(r)具有相同的表达内容。这是一个值得注意的事,因为一个r的矢量函数一般地说需用的三个标量函数来描述，警如用失量函数的三个笛卡儿坐标分最表示。另一方面，要说明@(r)只需r的一个标量函数。要注意表达式Φ(r）一常数表示三维空间中一个面。这类表达式的一个熟悉的例于就是描路径1S格径工三擀妆图4.1该装面s越的这干点产m图4.1,2所示两个等位面被包含它信法线简的利分路径丨利II的平而切过.62

述具有半径R的球面：*+9+2=R(5)电位为常数的那些面称为等位面。图4.1.2中所示是两个等位面的横截面，其中一个面通过r点，另一个通过r十△r点。如果把Ar看作微分失量，r+Ar点的电位和r点的电位相差一个微分量△Φ。这两个等位面不能相交。事实上，如果它们相交，那么r和r+Ar两点具有相同的电位，这就与我们的假设不特。图4.1.2中表示了从点r到点r+Ar所在等位面的最短距离An。微分几何学中设定，长度元An是与两个等位面都垂直的，由图4.1.2,AncosAr，可得A-cosr=on.r(6)式（6)中的矢量Ar可以是任意方向，它也其有任意的微分长度。确实，如果把距离An增大一倍，A@和Ar也将增大倍;△@/△n则保持不变，因此式（6)对任何（微分长度的)Ar都适用。我们得出结论，式(6)对于任何由r出发的微分矢鼠长度元Ar，斌予了一个标量，它的值正比于Ar 的量值，也正比于△r和单位失量n之间的夹角的余弦。这种对于失量的标量赋值可以表示为由失量长度元 Ar 与一个量值为 AΦ /△n方间为 n 的失量的标量积。也就是说，式(6)等价于A@grad@.Ar(7)其中电位梯度定义为grado=4n(8)因为式(8)与任何特定的坐标系无关,因此它提供了使梯度算子概念化的最好方法。同样的方程提供了在任何特定坐标系中所表示的gradΦ的算法，例如，在笛卡儿坐标系中有(9)r=ain+yi,+zi;Ar-Arir+Ayi,+Azig同时，对式(6)中Φ的微分变化的另一种表达A0(r+r,9+Ay,z+z)-(a,y,2)(10)A鉴于式(9)，这个表达式可写成=++)r=r(11)由此得出，在笛卡儿坐标系中，由公式(8)定义的梯度运算式为grad-i++(12)这里，引入了式(2.1.6)中定义的個三角形算了，作为表示梯度算子的另一种方式。本章最后的习题是作为例子以说明如何在其他坐标系中可以用类似的方法确定梯度，所得结果汇集于本书最后的表「中。·70

我们现在将证明电位函数Φ(r)可唯一-地确定E(r)。根据式(4),从点r到点r+Ar,电位变化为A=(r+Ar)-Φ(r)--*" .ds+f(13)Edsfr+srE.d式(13)中,前两个积分是根据Φ的定义公式(4)得来的。意识到ds就是Ar,且Ar是微分长度,因此,可以认为在失量 Ar 的这段长度中 E(r)是常量,则式(13)中最后的积分变为A@--E.Ar(14)失量元Ar是任的。因此,比较式(14)和式(7)，表明(15)E--Vo若给定电位函数@(r)，相关的电场强度就是Φ的梯度的负值。注意到我们还得到了一个有用的积分定理，因为如果把式(15)代人式(4),就有(16)f. p.ds=(r)-o(r)也就是说，电位梯度的线积分就是两端点间的电位差。当然，Φ可以是任何标量函数。回顾一下，我们能发现，由式（15)表示的E保证了它是无旋的，因为欠量恒等式(17)V×(v0) =0成立。标量位Φ的梯度的旋度为零。因此，给定一个按式(15)由电位表示的电场，那末(4.0.1)式自动满足，因为以上的讨论表明，电位@包含了有关电场E的全部内容，所以用grad@取代E构成了(4.0. 1)式的一个通解或积分。 一阶常微分方程的积分会产生一个任意积分常数,而一阶矢量微分方程curlE=0 的积分产生一个标录的积分函数Φ(r)。迄今，我们还没有对参考点r有过任何详细的说明。假如无穷远处电位的特性合适的话，通常把参考点设在无穷远处往往是很方便的。但对于一些特殊情况，这样选择参考点是不可行的。所有这些特例，都是涉及无穷大电荷量的问题。这种情况的一个例子是1.3节中第二个图例说明，由一个在士2方向延伸到无穷远的电荷分布所建立的电场。这个电场以反比于与带电区域的径向距离的规律衰减。因此，E的线积分即式(4),将从有限距离积到无穷远，涉及到(nr在两端点对应值的差值。如果一个端点移到无穷远，积分值就变成无穷大。对于延伸到无穷远但是不出现这类奇异特性的问题，我们仍假定参考点在无穷远处。例4.1.1等位面考虑与≥无关的电位函数(9)(18)(a,n-.+71

等位面可以用任何“！平面中的横截面图形来表示，在这些图中它们以图4.1.3所示的曲线出现。时干由式(18)给出的电位,在-平面中它的等位线是双曲线族。通过点(a, a)和(一a,一)的等位线的电位为 V, 而通过点(a,一a)和(一a,a)的等位线的电位为-Vn。E的量值正比于与等位面垂直方向上@的空间变化率。因此，如以相同的电位增量作出等位面，如图4.1.3中所做的(图中电位增量是 V。/4),则E的最值就与各等位面间的距离成反比。等位线的问隔越近，电场强度越高，图4.1.3中的电场线的箭头，总是从高电化指向低电位。注意到到由于电场线总是垂直于等位面，自然地在电场强度最大的地方，电场线的间距最小。例4.1.2梯度和线积分的求佩图4.1.3由式(18)给出的二维电位的管位面的横截面图我们的日的是通过直接计算作示例来说明在两给定点之间无场的线积分与积分路径无关的事实。特别是，考虑由式(18)给定的电位,鉴于式(12),电场强度可表示为E--v--K+)(19)我们将这个失量函数沿着图4.1.3质示的连接(1）和(2)两点的两条不同路径进行积分。对第一条路径Cs保持=a不变，因此 da=dziz。这样，积分式成为(20)[ E-da-' r,(r,a)dr --Loadr--2V对于第二条路径C,-a=0,通常ds=dzi十Ggin，因此所求积分为(21)I..E-ds-f..(Erda+E,dy)但是,对路径C,我们有 dg-(22)dz/a=0,因此式(21)变为Se E-ds- f.(B.+)drV(+22)dz=—2V(22)由于 E是通过取Φ的负梯腹求得的,因此是无能的,因而对于(20)、(21)两式给出相同的结果就不足为奇了。例4.1.3球形电荷云的电位均勾的静电荷分布P占有一个半径为R的球域。其余空间没有电荷（当然，无穷远处的平衡电荷除外）。下面将详细说明分片连续电位函数的确定。电荷分布的球面对称，使电场也是球面对称，因此可以根据商斯积分定律确定。接按照例1.3.1中的同样方法，求得电场强度为cR(24)· 72

为了求出内部区城的@，积分先是在球外区成进行，定处式（24）的值）然后选入半径为T的球内区裁可得(() -4-p(R)+%(r-r)(25)在电荷分布区的外部≥R处，电位民有点电荷的库仑电位形式(26) 注意4是净分布电荷。二维无旋场的形象化一般来说，等位面都是三维的表面。因此，任何恒定电位的二维图形都是这些等位面与某个给定平面的交线。如果电位的依从关系是二维函数，那未等位面就是柱形。例如式（18）表示的二维电位，其等位面具有如图4.1.3所示的双曲线截面的柱面我们复习这些几何概念是因为我们现在介绍一种有助于描绘二维场的不同观点。在画出的三维图形中，第三维用作表示电位@的幅度。这种图如图4.1.4所示，图中以式(18)的电位作为例子。三维图象的底面是-平面，而垂直的那一维坐标代表电位。恒定电位的等位线用恒定商度的线表示。Sr-V图4. 1.4以三继形式表示的式(18)和图 4,1.3 的二维电位，乘直坐标代表电位，类似于一张向上瓷低的潮紧的蘑膜。等位线族是薄跟表面一定高度的等高线族图4.1.4的表面可以看作是一张仲展在位于感兴趣区或周界的支架上的薄膜，这些支架随若边界电位的变化而成正比地抬高或降低。根据梯度的定义式(8),电场强度线总是沿着这个表面坡度最陡的下降轮廓线上。在人们的心目中，等位面是最有意义的，它能把二维电位画成好象一张等高线图，而电场强度线好象水从山上流下形成的水流线。4.2泊松方程给定E是无旋的，即式(4.0.1)，并给定高斯定律式（4.0.2)中的电荷密度，那末电场强度的:73

分布又是怎样的呢？由4.1节我们知道，通过用标量电位@表示矢量E。E--O这两个方程中的第一个方程同样可以得到满足。也就是说，由于引人了这种关系，式(4.0.1)已经被积分。在把式(4.0.1)积分后，我们把它放一下，集中解决第二个电准静态方程，即高斯定律。将式(1)代入高斯定律式(1.0.2),给出V.0--PE上式等同于70=-(2) 给定了方程右边的电荷密度，对这个标量的泊松方程进行积分，就是本章剩下的任务。类似于电路理论中的常微分方程，方程右边的电荷密度就是“激励函数”，在方程左边的是由式(2)的第二种形式表示的算子，称为Φ的拉普拉新。在笛卡儿坐标系中，由散度和梯度算子的表达式，即由式(2.1.5)和式(4.1.12)可得++--℃(3)+圆柱坐标系和球面坐标系的拉普拉新算子将在习题中求得，并汇集在本教科书最后的表！中。在笛卡儿坐标系中，这种算于表达式中的导数具有常系数。而在另外两种坐标系中，有些系数是随着空间变化的。注意在式(3)中，时间并不作为一个独立的变最出现。因此，求解一个随时间变化的电荷分布p(r,t)在时刻t。的准静态电场的数学问题与求解不随时间变化的电荷分布p(r）的静电场问题是相同的，只是p(r)等于p(r,t=to),即随时间变化的电荷分布在特定时刻t。时的值。在电荷分布已经给定的问题中，求解准静态场的值就等于求解一系列我们感兴趣时刻的不同电荷分布情况下的静态场问题。这里，我们强调这点，是为了说明静电场的求解比人们预先设想的具有更广泛的应用：每个静电场的解表示在一个特定时刻拍的一张“快照”。说了这么多，我们不需要电荷密度和电场的明显时间依从关系，而是说，只是在为了清楚有此要求时，应该这样做。4.3叠加原理正如式(4.2.3)用笛卡儿坐标系举例说明的那样，泊松方程是联系电位@(r)和电荷分布p(r）的线性二阶微分方程。所调“线性”是指微分方程中各导数的系数不是应变量Φ的函数。泊松方程是线性的一个重要推论是Φ（r）服从叠加原理。认识到这与电路理论中线性常微分方程服从叠加原理的相似之处是很有帮助的。叠加原理可以说明如下。考虑两个不同空间分布的电荷密度p.(r)和ps(r)。这两个电荷分布也许归属于不同的区域，或占有同一个区域。假设我们已分别地求得相应的电荷分布分别为p，和Ps并满足泊松方74

程(4.2.3)的电位中。和中。由定义V'0.(r)= -p.(r)(i)1'0)(r)=-h(n)(2) 把这两式相加，得(3)"0.(r)-V'D.(r)=-[p.(r)+ p(r))内为拉普拉新运算中要求的导数，例如式(4.2.3)中二阶导数，无论是先对各个电位求导然后相加，还是先把电位相加再进行求导，其结果是相同的，因此式(3)还可写为,(r)+(r)]=-1p.(r)+p(r))(4)由式(1)、(2)和(4)得登加原理的数学表达式。即,如果.o.(5)p0那末(6)parpb-ΦlΦ由电荷分布的叠加而产生的电位分布，等于与个别分布相关的电位之和。4.4与电荷奇异性相关的电场本节的任务至少有三项。第一，举例说明4.3节的叠加概念。第二，开始处理不是非常对称的电场，用图形表示这类电场时，电位是非常有用的，因此我们继续深入讨论用图形表示电位和出场分希的方法。最后,研究出的电位函数在以后各章中还会多次出现。象这节描述的，泊松方程在整个空间的解将证明是在没有电荷的子域中拉普拉斯方程的解。因此，在拉普拉斯方程起重要作的第 5章中，还将用第二种观点来讨论。首先，考虑与位于球坐标原点的点电荷相关的电位。电场可以应用1.3节中的高斯定律的积分形式式(1.3.12)求得。根据电位的定义，即式(4.1.4),可得点电荷的电位为(1)@=Ane这个对于三维泊松方程的“冲击响应”是公式推导和问题求解的出发点，是值得记住的。下面考总与分别位于z轴上a/2和一d/2处的一个正电荷和一个负电荷相关的电场，其图形e示于图4.4.1。式(1)中，是观察点与电荷之间的标量距离。用P表示观察点的位置,在图 4. 4. 1中这两个距离用r和r来表示。根据式（1)和图44.12轴上大小相等，符号相反的两个点电存75

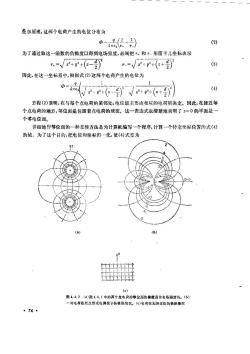
叠加原理，这两个电荷产生的电位分布为/11)(2) D-A()为了通过取这一函数的负梯度以得到电场强度，必须把1、和"-用笛卡儿坐标表示r=/249+(e+号)=/2+9+(c-%)(3)因此，在这一坐标系中，根据式(2)这两个电荷产生的电位为D=(4)Ve-+(s-号)e+g+(a+方程(2)表朗，在与每个点电荷的紧邻处，电位值主要由相应的电荷所决定。因此,在接近每个点电荷的地方，等位面是包围着点电荷的球面。这一表达式也清楚地表明了“=0 的平面是一个零电位面。详细地作等位面的一种直接方法是为计算机编写一个程序，计算一个特定丛标位置的式（4）的值。为了这个日的，把电位和坐标归一化，使(4)式变为c)图4.4,2(2)图4.4. 1中的两个点电荷的等位面的横裁面新电场强度线。(b)一对电荷在原点形成电偶极子的极限情况。（e)电在无限远处的板限情况76

(5)D+(-)()是方便的。式中4一号→鱼(/4ade)通过对不同的坐标位置求Φ值的方法，就有可能以多次计算的方式找到给定等位面的坐标位置。图4.4.2a的等位线就是在=0的条件下画出的。当然，等位面实际上是三维的面，它们可以由图示的曲线绕轴旋转得到。出于E等于中梯度的负值，电场强度线是垂直于等位面的。因此，电场强度线能很容易地画出，并在图4.2.2a中用带篇头的曲线表示。位于原点的电偶极子式(2)的一个重要极限相应于远离两个点心荷的观察点来看场的情况。这是一个非常重要的极限，因为符号相反的电荷对是极化了的原子或分子的模型。因此电偶极于将是第 6 章的中心,在那里，我们将讨论可极化物质。正常情况下，取偶极子的极限就是认为当》时，观察点和各电荷的连线基本上平行于『坐标。图4.4.3中表示的图4.4.3远离电偶极子处，从电荷到观察点的射线基本上平行于坐标近似几何关系可引出以下近似(6)T.二r十号coso+r---cos0;由于表达式中第一项比第二项大得多，"，和"-的乘幂可以展开成二项展开式(7) (a+b)"=a"+na"-lb+.于=—1,式(2)可近似为9ol...(-2.s..(8)qdcosoT.Eo记着，这一电位是用球坐标描述的。假设要绘制的等位面图形是在某个特定的位置通过“轴。当我们沿+方向移动时，电位的形状将是怎么样呢？式(8)的左边是定值。当0增加时，公式右边的余弦函数减小。因此，要停留在这个等位面上，从原点到它的距离r必须减小。当角度趋向元/2时，余弦值减小到零，很明减，等位而必须趋近原点。等位面和相关的E线示于图4.4.2b中。电偶极子模型可以从数学上确切地定义为，当两个等量异号电荷的量值不断增大而被此间77