《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第9章 磁化

第9章磁N9.0引言第8章中所考虑的磁场的源是与通过材料的不成对电荷载流子的运动相关的传导电流。典型地，电流存在于某一金属中，而载流子是传导电子。在这一章中，我们将认识到材料还能提供另一种磁场源。这些就是永久磁铁磁场以及插人磁化材料后会使线圈的自感增大的原因磁化效应是由于物质的原子组成倾向于具有像磁偶极子的作用。把绕核旋转的电子想像成一个环行电流并且因此产生与例题8.3.2所讨论的电流环相似的磁矩是很自然的更使人惊奇的是已求得的单个电子的磁偶极矩。这个与电子自旋性质相关的磁矩被定义为玻尔磁子m=±易专(1)这里e/m是电子的电荷质量比，其值为1.76×10"C/kg，而2元元是普朗克常数，寿=1.05×10-3J.s，因此m。的单位是A·m。原子和分子的量子力学告诉我们，无论是出于轨道运动还是自旋运动，电子对它们的净磁偶极矩的贡献趋于相互抵消。能作出贡献的这些电子典型地是在一未填满的壳层内如果材料的每个原子或分子只贡献一个玻尔磁子，所导致的磁矩的估算表明来自构成一种典型固体的全部电子的轨道运动和自旋运动的献最好是趋于抵消，或者合成场效应确实很人。即使图9.0a）半径为R的环形电流：给出磁偶摄使每个原子或分子只贡献一个玻尔磁子的磁矩，华径为R的球形材料的磁偶极矩计它所产生的磁场也是可以与一个极强的传导电流近似为各个原子的磁偶极矩之和产生的磁场相比的。为了使这点明显，可把一半径为R载电流i的电流环(图9.0.1a)的磁场和堆积在球形域中（图9.0.1b)只有一个电子磁矩的偶极子的磁场相比较。在球形材料中，我们认为净磁偶极矩简单地是单个分子的磁矩m。乘以分子个数。每单位质量中分子的个数是阿伏伽德罗常数（Ag=6.023×102°分子数/千克·摩尔）除以分子重量Mo质量等于体积乘以质量密度p(kg/m)。因此，对于半径为R的球来说，磁偶极矩的和是m=m(ganp)(A))(2)4y假设图9.0.1中电流环的半径与球的半径B相同，多大的电流；将会产生与假想材料球相同的磁偶极矩呢？如果让(8.3.19)式给出的电流环的磁矩m-iaR等这个球的磁矩(2)式，山此可得出电流；必须是·275

i=m.np e.(3) 因此,对于铁(这里 p=7.86×10% 和 M。=56)和 10 cm 的半径来说,产生相同的磁矩所需要的电流是10°A。材料的磁化或者是永久性的或者是由施加外磁场而诱导的，与第6章中讨论的可极化材料是很类似的。在多数材料中，能够起作用的每个分子平均磁短远小于一个玻尔磁子。然而，强磁化材料能够产生可以与(2)式中由估算而得的磁矩相比较的净磁矩。本章中有关磁化的讨论与第6章极化的讨论相类似，正象6.1节中使用极化强度来描述电偶极子对电场的效应一样，9.1 节中引入的磁化强度将说明磁偶极子对磁场强度的贡献。 此外,9. 2 节中总结的 MQS 定律和连续性条件是以后几节的基础,也是第 10 章的基础因为永久磁铁是如此普遍，所以9.3节所讨论的永久磁化场比6.3节所讨论的永久极化电场要熟悉得多。类似地，当一块铁被引人磁场中时，它所受的力是9.4节的构成定律描述的感应磁化的普追证明。极化和磁化间的广泛相似性使得第6 章中的大部分例子类似于磁化例子。这在所考虑的材料的磁化强度与磁场强度线性相关的9.5和9.6两节中尤共是如此。因此，这几节不仅建立在前面关于极化几节中得到的结果之上，而且也给出了展开这两个专题的机会。9.7节中所考虑的磁路有着很大的实用意义，它作为示例说明了有强磁化材料存在时场计算的近似方法。磁化材料的饱和有着重要的实际意义。9. 6 和 9.7 两节的问题是磁非线性材料中磁场的人门。在 9.2节中,我们将把法拉第定律加以推广,使它能在这一章中用于预测包含有磁化的系统中的线圈的端电压。这一推广形式将在9.5节中用来确定包含磁化的终端关系。在以后几节中的例子将研究涉及磁化时法拉第定律的含意。像在第8章中一样，在这一章中我们只限于讨论能用完纯导电电路的端口变虽来模拟的例子。在9.2节中推广的包含磁化的MQS定律，构成了讨论第 10 章的主题MQS系统中电场的基础。9.1磁化强度物质中磁场的源是一些(或多或少地)作整齐排列的单个电子的磁偶极子或者是环行的电子引起的电流①。 我们现在来描述代表材料的磁偶极子分布对磁场的作用。在8.3节中，我们定义一面积为α载有电流：的电流回路的磁矩m的大小为m=ia。磁短失量被定义为与跨越电流环周线的表面相垂直且其指向决定于右手螺旋规则。在8.3节中，磁矩是沿球坐标系中的方向，已求出了电流环产生的磁场强度是H=nm[2cosoi,+ sin oiJ(1)这个磁场类似于与偶极短为P的电偶极子相关的电场。当的方向沿≥轴时，取(4.4.10)式的①对磁场起的作用可能类似于电药对电场起的作用的磁单极子实际上是可能存衣的，很是无疑役有工程意义。见Science Hesearch News,"In Search of magnatic monopoles",Vol.2l6,P.10s6(June4,1982).276 :

梯度即可给出电偶极子的电场(2)[2cosbi,+singi]E=Ane0因此，利用下列替换(3)>μompe即可从一种偶极子的场得到另一种竭极子的场，在6.1节中，电偶极子的空间分布是用极化强度P=N?来表示的，其中N是偶极子的个数密度。类似地，这里我们定义磁化强度为M=Nm(4)式中，N仍然是每单位体识中的微子数目。注意正像偶极矩力的类比最是uom一样，极化强度P的类比量是pM9.2涉及磁化时的定律和连续性杂件回想-下，电偶极子的空间分布对电场强度的彪响是由电场高斯定律的推广（6.2.1)和(6.2.2)式来描述的。(n)V.e,E--v.P+pu现在滋偶极子的空间分布对磁场强度的影也可类似地考虑用推广的磁通连续性定律uH--HM(2) 来描述。在这个定律中，没有与不成对电荷密度相对应的类比量。在包围具有法线n的交界面部分的增最体积上对(2)式积分可求得连续性条件n·μ(H--H)--n·μo(M-M)(3)根据对于极化的描述的类比性，(2)和(3)式右边的量可分别定义为磁荷密度P㎡和磁荷面密度m:(4)[Pu=-V-oM.(5)am=--nμo(M-Mh)包含磁化的法拉第定律磁通连续性定律的修正，，意味着麦克斯书方程组的另一定律也必须要加以推广。在1.7节引人磁通连续性定律时，我们发现它在法拉第定律中几乎是固有的。因为旋度的散度恒等于零，1所以法拉第定律的自由空间形式的散度简化为(6) V(VxE) 0---%(μH)+277

于是,在自由空间中，u.H 必须有一个至少是不随时间变化的常数的散度。磁通连续性定律又加J:这个常数应该是零的信息。在磁化材料存在时，(2)式表用量 μo(H+M)是无散的。为了使法拉第定律与这一要求相一致，现在这个定律可写成V×E=-%Cu(M+H)(7)磁通密度法拉第定律中 H 和M的组合及磁通连续性定律使我们自然地要定义一个新的变量，即磁通密度BB=μ(M+H)(8)这个量起着类似于(6.2.14)式定义的电位移通量密度D的作用。因为不存在宏观的滋荷单极了，所以B的散度是零。也就是说，磁通连续性定律式(2)，简单地变成v·B=0(9)而相应的连续性条件(3)式变成(10)n.(B*-Bb)=0用磁通密度表示法拉第定律可得到相类似的简化,方程(7)变为xE--aB/at(11)如果磁化被规定与H无关，通常最好直接在公式中引入M而不要引入B.然而，如果M作为H的函数给出，特别是如果它是H 的线性函数，最方便的方法是把M从公式中移出而使用B作为变量。考虑磁化时的端电压在我们讨论完纯导电线圈的端电压的8.4节中，不存在磁化。为了要包含磁化而推广法拉第定律要求端部关系也应被推广。前面导出端部关系时的出发点是法拉第积分定律(8.4.9)式。通过用B代替μoH，这个定律可被推广到包含磁化效应。另外,端部关系(8.4.11)式的导出是与前面相同的。因此，端电压仍是(12)但现在的磁通链是=],B-da(13) · 371

在9.4节中，我们将看到法拉第电磁感应定律，像这最后两个关系式所反映的，是测量B的基础。9.3永久磁化作为曾在古代使磁场的存在明显化的天然磁石的现今变型，永久磁铁今天是如此廉价地被大量制造，以致在家庭中被用来把注意事项钉在电冰箱上，并且可靠到可以用在电机、传感器和信息存贮系统的心脏部位。作为基本近似，一个永久磁铁可被模拟成有着特定分布的磁化强度M的某种材料。因此,在这一节中，我们将考虑由给定的M分布所产生的磁场强度。在没有电流密度J的区域中，安培定律要求H是无庭的。于是，用8.3节中引入的标量磁位甲来描述磁场强度常常是方便的。H----(1)从通量连续性定律(9.2.2)式，可接着导得甲满足泊松方程(2)V-uoM-pm/μoipm一规定的磁化强度可导致一确定的磁荷密度Pm这种情形类似于6.3节中所考虑的情况，在那里极化强度是预先给定的。结果是，P，是已知的。当然，磁化物体中的净磁荷总是等于零，这是因为如果在包含物体的全部体积中进行积分，-μ.H-da-0(3).Pmdu=第4 和第5章中阐明的在给定电荷分布下求解治松方程的技术可以直接应用于这里。例如,如果给定了整个空间的磁化强度并且不存在其它源，则标量磁位可由重叠积分给出。正如(4.2.2)式的积分是（4.5,3)式一样，(2)式的积分是 2(4)Y如果所研究的区域是由其上的边界条件已规定的某一种材料界定的，则（4)式提供了特解。例 9. 3. 1 均勾磁化围柱体的磁场强度图9.3.1中所示的圆柱体沿方向被均勾磁化，M=M。t。为了求出圆柱体内部和周国自由空间内的磁场 H,第一步是先计算磁荷密度的分布。均勾分布的 M 没有散度，因此在整个体积内 P=0。这样,H 的源是在发出和终止M 线的表面上。考虑到(9.2.3)式，它取面电荷密度的形式(5)Om=-n.po(M--Mb)-±uM.上、下特号分别归属于上、下端面原则上说，我们也能够应用重登积分求出别处的标量磁位。为了使积分简单起见，我们这里只限于求出轴上的值。这样，（4)式的积分化为在阅柱体的两个端面.工的积分uM.2npdooM,2np'dW-I. AA.Nt2)(6)4mμp"+(z+d/2)如巢使用绝对值使表达式不管沿2轴的位置如何都行效，则这些积分成为· 279

（a）没种向均匀磁化的圆挂体。（b）标量磁位的轴肉分布和39.3(c）轴向磁场强度。对于这些分布，圆杜体的长度均假定等于它的直径。4[()+(-)-/--()+(+)+/+](7)由（1）式可得磁场强度(2/a-)(z/d+号)H-(8)() +(e/a+)[() +(e/a-)式中,当12|>号时，≥0 和当[=1<号时,=2。这里，从上到下，符号分别相应于计算上端面上方的场，磁铁内部的场别下端面下方的场，3.1中所示更和丑，的轴向分布是与起始于磁铁顾面而终止于底面的场的三维图形相一致的。对于球形磁铁(这与图 6.3.1所示的永久极化球相类似),磁铁内部场强度的方向是与M 的方向相反的。实际上，M最可能是通过测量出外部场，然后由这个场推演出M来得到确定的。如果磁场强度是由给定的电流和永久磁化共同产生的，可通过把电流和磁化两者引起的磁场的叠加来计算总磁场。例如，假设图9.3.1的均勾磁化圆柱体被图8.2.3所示的N匠螺线管围绕。那么，轴向磁场强度将是电流的磁场［由毕奥-沙伐定律(8.2.7）式给出门与磁化磁场［由(4)式的负梯度给出}之和。例 9,3. 2 双存在磁带中的信号的恢复在愈式录音机中，永久磁化披用作永久记录。电磁铁中的电流被用于诱发求久磁化，即在某种材料的磁化中开发磁潜，像将在 9.4节中讨论的一样。这里，我们考虑垂直磁化模型，一个积极从事的研究领城。传统的记录方法是通过产生平行于磁带的化强度来实现的。在静止的薄带中,假设图 9.3.2 所示磁化强度在厚度上:是均勾的且具有如下简单形式M-MacosBri,(9)首先要确定附于磁带的参考系中(记为(3,3,2),如图 9.3. 2 规定)的磁场。磁带以速度U相对于固定读头运动。因此,我们的第二步将是用固定坐标来表示这个场。从图 9. 3. 3 可清慧看出,这些记为(s,孕，2)的坚标与运动坠标间的关系为(10)-tly=yr+Ut因此，从固定参考系看来，磁化强度取行波形式(an)M=M,cosp(r"--Ut)i,1.289

288图9,3.2永久磁化的磁带具有表示一被记图9.3.3从读头线围的参考系可以爱出，录信号的停里叶分盘的 M 的分布。 从附于避带沿方向以迷度运动磁带上的参考系来看,磁化强度是静态的。如果在一固定位置”观察 M，它以频率の=PU 作正兹形时间变化。周定参考系频率和空间周期性问的这神关系使人想起磁化分布是怎样通过"记录"一频率为)的信号而建立的磁化强度在磁带体积中没有散度。因此，场源是面磁荷密度。如果用上、下符号分别来标记磁带的上、下表面，由此可得(12)a=土uM.cosB在上、下表面所需满足的连续性条件表示磁通的连续性(9.2.3)式μ.H,-μoHp poM,cospr在一号(13)μH-H--μeMgosBa在y--号处及切向H的连续性W,=甲。在1一号处W一W在一一号处(14)另外，当 y→±co 时,场应趋于零。因为场源被限制干两表面上，所以在由交界面所界定的体积区城内，标量磁位一定满足拉普拉斯方程，即=0 时的方程(2)。受到源关于 y=0 平面的奇对称及沿 a 方向的周期性启发，我们选择在磁带的上方(a),内部(0)及在下方(b)三个区域中标量磁位拉普拉斯方程的解，它们也满足奇对称条件甲(g)=--甲(一)。W.-Ae-wcosprW,-OsinhpyensBr(15)W-AeycosBa在 β>0 的要求下,外部的位在 -士o处趋于零。通过剔除拉普拉斯方程解中的 cosh(βy)cos(βt)，可使内部的位函数是9的奇函数，同时可通过使系数等值异号而使外部函数成为一奇函数。这样，只有两个系数尚待确定。这费可通过将假设解代人(13)式或(14)式的任一个，然后解这两个方程可得到s-Mgo(1+cotheg)c-[(++coth)sin B(16)在一个交界面上边界条件能自动满足，如果它们在另一交界而！：被满足的话。这就是假设解确实正确的一个验证。我们把轴的原点取在对称面以及选取里为3的奇函数解的预见使得待定系数的个数由4个少到2个。现在，把这个场表示在固定的坐标系中。利用(16a)式定义的A以及由(10)式根据固定垒标系给出的和则磁带上方的标量磁位已确定为·281 +

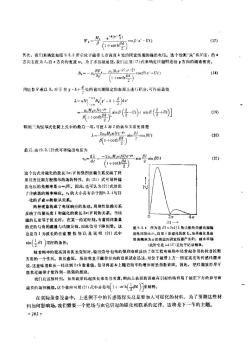
-(0-2)=sf(t-U)(17)(1-FcothBd)其次，我们来确定如图9.3.3所示位于磁带1：方高度五处的固定线图的输出电压。这个检测"头”有N匝，洛*方向长度为 1,沿z方向的宽度 w。 为了求出磁通链,我们应用(17)式来确定线图附近沿9方向的磁通密度。B,Me-yr-)(18)B,--1cosp(r"--Ut)1+cothe用迹数N乘以B，对于在-h+兴处的被线周限定的表面上进行积分，可得微通链A-oNT"B(g+++号)dr H.MawNer.(19)[sinB(-0)-1 sinB(+)]B(1+coth利用二角值等式化简上式中的最店项，可使入对1的依从关系更清地2uMwNesin cos pUt1(20)B(1+coth最后，由(9.2.12)式可得输山电压为--2pMwNPadaenBLsinput(21)(1+coth)这个公式对磁化的波长2元/β的强烈依赖关系反映了利用拉普拉斯方程预示的场的特性。由（21）式可导得输出电压的角频率是の=BU。因此，也可认为(21)式给出了传感器的频率响应。%的大小具有示于图9.3.4与归-化的 β或α的依从关系。两种现象构成了电压响应的基础。周期性依赖关系反映了线圈长度 1和微化的被长2元/β 闻的关系。 当线时，在某一给定时刻,有着同样数量圜的长度等于波长时的正的与负的磁通与线围交链，因此信号下降到零。这图 9. 3. 4 作为是 B1=2元1 /1的函数的传感线国输也是当！为波长的任意整数倍以及说明（21)式中出电压的大小。这里人是磁化的波长。如果磁化是由受角频率为的激动的固定线圆产生的真水平轴sin(βl)项时的条件。此时它基随着频率的提高因面泌长变短时，输出信号包络的强烈衰减反映了在工程电磁场中经常起作用的拉普拉斯方程的一个性所。 波长愈短，场沿垂直于磁带方向的衰减就愈迅速。对位于磁带上方一-固定高度的传感线医来说，这意味着被长一经达到 2xh 数量级，信号将基本上随着频率的增加而呈指数衰减。因此，把线圈放得尽可能靠近磁带才能得到一很强的激励。我们应该预料到，如果磁带比起波长来是非臀薄，则由上表面的面磁荷引起的场将道丁被正下方的异号面磁荷的场相抵消,这个数应可用(21)式中分母项[14:0h(一8a))来解释。在实际录音设备中，上述例子中的传感器探头总是要加入可磁化的材料。为了预测这些材料如何影响场，我们需要一个把场与由它引起的磁化相联系的定律。这将是下一节的主题。282:

9.4磁化构成定律0.3节中的承久醛化模型多少象是与磁场强度无关，确定了磁化强度M的人为的例了，即使在最好的永久磁决中，M实际上总是有些依赖于H的。构戏定律使磁化强度M成滋通密度B亏材料内的宏观H相联系。在讨论一些更普追的关系和它们的基础物理现象前，做一个能给出磁化构成定律直接证明的实验是很有好处的，其日的是观察电流据安培定律建立H的过程，以及按照法拉第定律B感应出的电压来推导出B。例9.4.1输环形线图钩环形线圖示于图9.4.1中。它由一个在培充有磁化材料的辐环形铁心边缘上紧绕的N，随线圖构成。借助丁一个激励端子的电源，这线竭将载有电流。可以假设最终的电流分布是如此平稳，以致由导线的有限尺寸所引起的场的细微结构可以忽略。我们将忽畴线圈微小的螺我间距，和相关的沿围绕罐环轴线环行的小电流分量。锈环的轴1图9.4.2为确定图 9.4. 1所示线图中的 H,把图9.4.1含科的锡环形线圈由周线℃包留的丧面S用于安培积分定律。由于几何形状是锡环形，磁化材释中的H场可以通过安培定律和对称性的考虑来确定。关于锅环轴的对称性提示了H是沿中方向的。把MQS 安培定津的积分形式应用在钙环内一半径为的间绕缓环轴的周线 C上。因为环形线圈的主半径丑比次半径大，我们将忽陷在环形线圈载面上的变化并丑用平均半径R来近似。这一周线所包围并示于图9.4.2的表前S被电流i穿过N，次，给出总电流N1。因此，磁心内部的方位角方向的场近似地为2uH,-NiH=H--(1)注意，相同的论证说明磁心外的磁场强度为零。一般说来，如果给定电流分布而希望确定H，这不仪求助下安培定律，而且也求助于磁通连续性条件。在理想化的钢环中，其中磁通线能不离开被磁化的材料而自动地自身闭合，则磁通连续性条件自然地得到满足。因比,在衡形结构中,施加在铁心 I:的 H 可以通过电流 和几间尺寸的测量来确定。我们怎样来测最磁心中的磁通密度呢t因为B出现在法拉第感应定律中，所以也是绕在不形磁心上的N随附加线圈的端电压的测量值可给出有关B的信息。这个线圈的端子接在一个足够高的阻抗上以使这个次级绕组中的电流可以忽酪。这样，电流，班建立的H场将保持不变。专感线阖每通交链的磁通近似地等于磁通密度乘以磁心的截而面积元W/4。因此，由传感线圈的端了所交链的磁通是A.-N.B(2): 283

所以，端了磁通链直接地反映了磁心中的磁通密度下面的演示表明(1)和(2)两式如何能从第一,个线圈的端电流和电压测新磁心材构白开米祥上磁化转性。演示 9. 4,1 B-H 特性的测定图9. 4.3中所示实验把磁化转性显示在示波器上，磁化材料数成携题 9. 4. 1 的萄环形,它受通有取自自耦变I器特电流i的 N,匠线困激励。根据(1)式,串联电阻两端的电压给出正比于H的示波器水平偏转。币数为N，的线圈的端钮通过一积分电路被连接到示波器的垂直偏转端钮。这样，垂直偏转正比于端电压的积分值或者入。因而通过(2)式也正比丁B图 9.4.3措绘正然稳态下,B-H 曲线的演示在以下关于磁化特性的讨论中,把材料想象成由这个实验中的镯环形磁心所构成是有益的。这样，磁场强度 H 正比于电流 ,而磁通密度 B被反映在与这个磁通相交链的一个线圈的感应电压中。许多材料是磁线性的,即M-x.H(3)式中~m是磁化系数。更一般地,磁线性材料的构成定律可用(9.2.8)式定义的磁通密度写成B=μH; μ=po(1+xm)(4)按照这个定律,通过材料的磁导率μ代替自由空间磁导率 uo 就考虑了磁化效应。为了比较各种材料的磁化能力,常常使用相对磁导率 μ/ uo表9.4.1给出了一些元素、化合物和常见材料的典型磁化系数。大多数常见材料是轻微可磁化的。某些容易极化的物质，例如水，却并不容易磁化。注意磁化系数既可以是正值也可以是负值,还有一些材料，著名的如铁及其化合物的磁化系数可以是巨大的。在建立某一材料能被期望的磁化能力的估价中，对它的微观起源有一个定性图景是有帮助的，从原子水平开始，但包括当它们变得象在固体中一样稠密时所引起的原子组或分子组的集体效应。在最易被磁化的材料中,这些后者的效应是主要的。一个原子（或分子）的磁矩是轨道和自旋的贡献之和。尤其在原子稀薄的空气中，磁化系数是由各个磁矩在磁场的作用下进行(部分地)沿线排列导致的。虽然自旋对磁矩的贡献趋于相互抵消,但许多原子仍有一个或数个玻尔磁子的净磁矩。在室温条件下,由于热运动，印使在最强的磁场下磁矩的取向大多数是随机的。结果是，外施场只有在很低温度下才能够引起有效的磁化。顺磁材料只有在低温下才显示出可观察到的磁化系数。如果在没有外施场时,自旋对一个原子的磁矩的贡献几乎抵消，则就它显示出一很小的负值磁化系数意义上来看，这种材料可以是抗磁性的。由于外施场的作用，轨道电子的环行稍许被改变，导致磁矩的与外场相反方向的改变。还存，热能趋于使这些磁矩方向杂乱。在室温条件下，这个效应比起对顺磁材料的效应要小。在非常低的温度下，有可能把外施场提高到某一值使得几乎所有的磁矩沿同一方向整齐排284*