西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第五章 准静态静电场

第五章准静态电磁场 5.0序 5.1电准静态场和磁准静态场 5.2磁准静态场与集总电路 5.3电准静态场与电荷驰豫 5.4集肤效应与邻近效应 5.5涡流及其损耗 5.6导体的交流内阻抗 5.7电磁兼容简介 E =yE, 0 H x

第五章 准静态电磁场

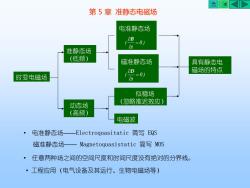
AKK第5章准静态电磁场电准静态场OB=0）at准静态场（低频）磁准静态场具有静态电磁场的特点aD=0)时变电磁场at似稳场（忽略推迟效应）动态场（高频）电磁波电准静态场-Electroquasitatic简写EQS磁准静态场一Magnetoquasistatic 简写 Mos·任意两种场之间的空间尺度和时间尺度没有绝对的分界线。工程应用（电气设备及其运行、生物电磁场等）

第 5 章 准静态电磁场 • 电准静态场——Electroquasitatic 简写 EQS 磁准静态场—— Magnetoquasistatic 简写 MOS • 任意两种场之间的空间尺度和时间尺度没有绝对的分界线。 • 工程应用（电气设备及其运行、生物电磁场等） 电准静态场 0 ) t ( =  B 准静态场 （低频） 时变电磁场 磁准静态场 0 ) t ( =  D 具有静态电 磁场的特点 动态场 （高频） 似稳场 （忽略推迟效应） 电磁波

合KKD5.1电准静态场和磁准静态场aB(=0)的作用，即E,~0，电磁场基本方程为低频时，忽略二次源电准静态场ataDdpV.B=0,V.J--VxH=J+atCVxE=0,V.D=p特点：电场的有源无旋性与静电场相同，称为电准静态场（EQS）。用洛仑兹规范V·A=-o/ot，得到动态位满足的微分方程VA=-w,Vp=-p/saD磁准静态场低频时，忽略二次源的作用，即H，0，电磁场基本方程为atVxH=J.V.B=0,V-J=0VxE=-oB/ot,V.D=p特点：磁场的有旋无源性与恒定磁场相同，称为磁准静态场（MQS）。用库仑规范V·A=0，得到动态位满足的微分万程V'A=-, V'=-p/8

电 准 静 态 场 特点： 电场的有源无旋性与静电场相同，称为电准静态场（EQS）。 用洛仑兹规范  A = − t ，得到动态位满足的微分方程  ,   /  2 2  A = − J  = − 低频时，忽略二次源 的作用，即 ，电磁场基本方程为 t D HD  0  = −   =     =  = E B D H J B J / t , , 0 , 0 特点：磁场的有旋无源性与恒定磁场相同，称为磁准静态场（MQS）。 磁 准 静 态 场 低频时，忽略二次源 的作用，即 0, ( 0 ) Ei  t =  B      =    =  = −    = + E D B J D H J 0 , t , 0 , t 电磁场基本方程为  A = 0  ,   /  2 2  A = − J  = − 用库仑规范 ，得到动态位满足的微分 方程 5.1 电准静态场和磁准静态场

AKK讨论与引伸EQS 与MQS 的共性与个性A.Q满足泊松方程，说明EQS和MQS忽略了滞后效应和波动性，属于似稳场。·EQS和MQS场中，同时存在着电场与磁场，两者相互依存。：EQS场的电场与静电场满足相同的基本方程，在任一时刻t，两种电场的分布致，解题方法相同。EQS的磁场按v×H=J+aD/at计算。MQS的磁场与恒定磁场满足相同的基本方程，在任一时刻t，两种磁场的分布一致，解题方法相同，MQS的电场按×E=-aB/at计算。·A.在两种场中满足相同的微分方程，描述不相同的场，为什么？a）A的散度不同，A必不相同，B=V×A也不相同；b）E=-V（EQS）和E=-Vβ-aA/at（MQS），表明E不相同

· A,  满足泊松方程，说明 EQS 和 MQS 忽略了滞后效应和波动性，属于似稳场。 · EQS和MQS 场中，同时存在着电场与磁场，两者相互依存。 · EQS场的电场与静电场满足相同的基本方程，在任一时刻 t ，两种电场的分布 一致，解题方法相同。EQS的磁场按 H = J +D t 计算。 · MQS的磁场与恒定磁场满足相同的基本方程，在任一时刻 t ，两种磁场的分布 一致，解题方法相同，MQS的电场按  E = −B t 计算。 · A,  在两种场中满足相同的微分方程，描述不相同的场，为什么？ b） E = − （EQS）和 E = − −A t （MQS），表明 E 不相同。 a）A的散度不同，A 必不相同， B = A 也不相同； EQS 与 MQS 的共性与个性

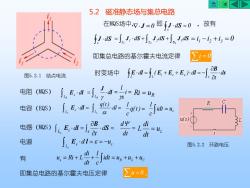
合KKD52元磁准静态场与集总电路在MQS场中,v.J=0即{J·dS=0 ，故有fJ.ds =J,Jrds+Js,Jds+J,Jds=i,-i, +i,=0i=0即集总电路的基尔霍夫电流定律aB时变场中 fE·dl-f,(E,+E.+E.)·dl =-.d图5.2.1结点电流atJ. E.dl =]., 二.dl ==i= Ri =uR电阻（MQS）AR[, E,dl= [, 9d= Lq(0)= idt=u电容（EQS）Sus）dyrdiaB.ds =C电感（MQS）JE,·dl=JI=uadtdt电源E.dl=8=-u,图5.2.2环路电压,= R+L+ [udt=ug+u,+te有dtCZu=0即集总电路的基尔霍夫电压定律

5.2 磁准静态场与集总电路 在MQS场中， J =0 即 d 0 ，故有 s  =  J S J dS s   J S J S J S S d d d 1 2 3 3 S 2 S  1   =  + + = i 1 −i 2 +i 3 = 0 即集总电路的基尔霍夫电流定律 i = 0 时变场中        = + +  = − L s i c e L d t d ( ) d s B E l E E E l 电容（EQS）  = Lc c E dl   = Lc dl s q(t )  q(t ) = c 1 c idt u c 1 =  电阻（MQS）   LR c E dl  =  LR dl J  = i = s l  R Ri = u 电感（MQS）  =     =  S B E l d t d L s i L = dt d L u dt di L = 电源 s L e d u s  = = −  E l  有 s R L C idt u u u c 1 dt di u = Ri + L + = + +  即集总电路的基尔霍夫电压定律  =  u 0 图5.2.1 结点电流 图5.2.2 环路电压

AKKD5.3电准静态场与电荷驰豫导体中自由电荷体密度随时间衰减的过程称为电荷驰豫5.3.1电荷在均匀导体中的驰豫过程设导电媒质，8均匀，且各向同性，在EQS场中J=D/8p+=0apV.J=-通解为p=peatGatV.D=p时的电荷分布，=6/式中P。 为=0 （驰豫时间），说明导电媒质在充电瞬间，以体密度分布的电荷随时间迅速衰减。EQS场中，导体媒质内的电位满冠"=-=-Poe0(r,t)=Jr Poeav = Po(r)e -特解之一为4元8说明在EQS场中，导电媒质中自由电荷体密度b产生的电位很快衰减至零。厨思考导电媒质中，以6分布的电荷在充电过程中驰豫何方？充电后，导电媒质的电位为零吗？

5.3 电准静态场与电荷驰豫 导体中，自由电荷体密度随时间衰减的过程称为电荷驰豫。 5.3.1 电荷在均匀导体中的驰豫过程 说明导电媒质在充电瞬间，以体密度分布的电荷随时间迅速衰减。 EQS场中，导体媒质内的电位满足 e t 0 2 e 1       −  = − = − e e t V 0 t 0 e dV (r )e 4 r (r,t )       − − 特解之一为 =  = 说明在EQS场中，导电媒质中自由电荷体密度  产生的电位很快衰减至零。 设导电媒质  , 均匀，且各向同性，在EQS场中 t   = −  J 0 t + =       通解为 e t o e    − = J = D /   D =  式中 o 为 t =0 时的电荷分布  ， e =  /  ( 驰豫时间)， · 导电媒质中，以 分布的电荷在充电过程中驰豫何方？ · 充电后，导电媒质的电位为零吗？ 

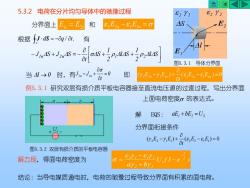
合D5.3.2电荷在分片均匀导体中的驰豫过程82Y26,Y1EASE=E26,E2n-8,En=0和分界面上J·ds =-oq/ at,根据有管dCAS-P,AIAS+P,A1S- Jin4S+ J2n4S =-at图5.3.1导体分界面do=0即当 △/ →0 时，有J2n-Jn(8,E2-8E)=0YEYE+at例5.3.1研究双层有损介质平板电容器接至直流电压源的过渡过程，写出分界面上面电荷密度。的表达式。解EQS:aE,+bE,=Us分界面衔接条件O(Y,E,-YE)+(,E,-6E)=0at图5.3.2双层有损介质的平板电容器0-E1-812U,(1-e解方程，得面电荷密度为aya+byi结论：当导电媒质通电时，电荷的驰豫过程导致分界面有积累的面电荷

5.3.2 电荷在分片均匀导体中的驰豫过程 结论：当导电媒质通电时，电荷的驰豫过程导致分界面有积累的面电荷。 分界面上 E1t = E2t 和  2 E2n − 1 E1n = 根据 s J  dS = −q / t, 有       + +   − + = − l S 2 1 l S 2 1 S t J S J S 1n  2n   1   2   当 l →0 时，有 0 t J J 2n 1n =   − +  即 ( E E ) 0 t ( E E ) 2 2n 1 1n 2 2n − 1 1n =    − +   解 EQS： 1 2 US aE +bE = 分界面衔接条件 ( ) ( ) 0 2 2 1 1 2 2 − 1 1 =   − + E E t  E  E   解方程，得面电荷密度为 U (1 e ) a b t s 2 1 2 1 1 2         − − + − = 图5.3.1 导体分界面 例5.3.1 研究双层有损介质平板电容器接至直流电压源的过渡过程，写出分界面 上面电荷密度  的表达式。 图5.3.2 双层有损介质的平板电容器

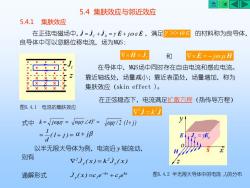
AKKD5.4集肤效应与邻近效应5.4.1集肤效应在正弦电磁场中，j=j+j，=E+jocE，满足0的材料称为良导体良导体中可以忽略位移电流场为MOS：VxH-jVxE=-joμH和在导体中，MQS场中同时存在自由电流和感应电流。文支-靠近轴线处，场量减小；靠近表面处，场量增加，称为XXX集肤效应（skineffect）。在正弦稳态下，电流满足扩散方程星（热传导方程）图5.4.1电流的集肤效应v'j=kj式中k= jouy=Voy45=o/2(1+j)(1+j)=α+F,=E以半无限大导体为例，电流沿轴流动，xJH则有V2j(x)=kj(x)j,(x)=c,e-a+c,e图5.4.2半无限大导体中的电流J的分布通解形式

5.4 集肤效应与邻近效应 在正弦电磁场中， ，满足 的材料称为良导体， 良导体中可以忽略位移电流，场为MQS： J  J  J  E  E   j = C + D = +   C H J   =  E    H  和  = − j 在导体中，MQS场中同时存在自由电流和感应电流。 靠近轴线处，场量减小；靠近表面处，场量增加，称为 集肤效应（skin effect )。 在正弦稳态下，电流满足扩散方程（热传导方程） J J   2 2  = k 式中 k = j =  =   45  / 2 (1+ j ) = (1+ j ) = d 1  + j 以半无限大导体为例，电流沿 y 轴流动， 则有 J ( x ) k J ( x ) y 2 y  2  =  通解形式 kx 2 kx y 1 J ( x ) =c e +c e  − 5.4.1 集肤效应 图5.4.1 电流的集肤效应 图5.4.2 半无限大导体中的电流 Jy的分布

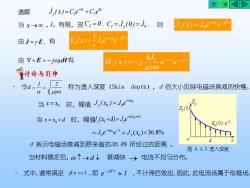
合KKDj,(x)=C,e-k +C,eb通解J,(x)=Je-ate-iBx当x→,j,有限，故C,=0,C,=j,(0)=J。，则E,(x)=1joe-axe-ipx由j=E，有k由 V×E=-ju有-axe-iBxH.(x)=uyo曾讨论与引伸2令d==称为透入深度（Skindepth），d的大小反映电磁场衰减的快慢aVuyoE当x=x时，幅值J(x0)=JeE,(0)当 x=+d 时, 幅值,( +d)=Je~α(btd)E,(0).e-=Joe-e-l=J,(xo)×36.8%CPd表示电磁场衰减到原来值的36.8%所经过的距离。图5.4.3透入深度当材料确定后，の个→d衰减快电流不均匀分布。式中，通常满足βx<<1，即e-iβ×~1，不计滞后效应，因此，此电流场属于似稳场

通解 kx 2 kx y 1 J ( x ) =C e +C e −  由 J  =  E  , 有 x j x y 0 J e e 1 E ( x )    − −  =  0 x j x z e e kJ H ( x ) j    − − = −  由 E H 有      = − j · 式中,通常满足  x 1 ,即 e − j x  1 ,不计滞后效应,因此,此电流场属于似稳场。 当 x → ， j y 有限，故 C 0 , 2 = C J (0 ) J , 1 y 0 =  =  x j x y 0 J ( x ) J e e − −  则  =  · 令 称为透入深度（Skin depth），d 的大小反映电磁场衰减的快慢。   1 2 d = = 当 x = x0 时，幅值 0 x y 0 0 J ( x ) J e − = 当材料确定后，   →d  衰减快 → 电流不均匀分布。 当 x = x0 + d 时，幅值 ( ) 0 0 0 ( ) x d y J x d J e − + + =  ( 0 ) 36.8% 1 0 0 = =  − − J e e J x y x d 表示电磁场衰减到原来值的36.8% 所经过的距离 。 图 5.4.3 透入深度

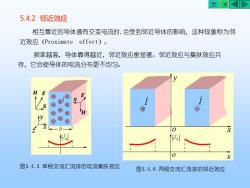
AKKD5.4.2邻近效应相互靠近的导体通有交变电流时，会受到邻近导体的影响，这种现象称为邻近效应（Proximateeffect）。频率越高，导体靠得越近，邻近效应愈显著。邻近效应与集肤效应共存，它会使导体的电流分布更不均匀。HHXKYXXXXO8H8X8+Xx0PP.0x图5.4.5单根交流汇流排的电流集肤效应图5.4.6两根交流汇流排的邻近效应

5.4.2 邻近效应 相互靠近的导体通有交变电流时,会受到邻近导体的影响，这种现象称为邻 近效应（Proximate effect）。 频率越高，导体靠得越近，邻近效应愈显著。邻近效应与集肤效应共 存，它会使导体的电流分布更不均匀。 图5.4.5 单根交流汇流排的电流集肤效应 图5.4.6 两根交流汇流排的邻近效应