《电磁场与电磁能》课程PPT教学课件（马冰然版）第二章 静电场 2.8 镜像法

第二章2.82.8镜像法原电荷镜像电荷2025-6-11

2025-6-11 第二章 2.8 1 2.8 镜像法   ? 原电荷 镜 q 像电荷

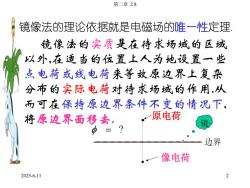
第二章2.8镜像法的理论依据就是电磁场的唯一性定理镜像法的实质是在待求场域的区域以外，在适当的位置上人为地设置一些点电荷或线电荷来等效原边界上复杂分布的实际电荷对待求场域的作用.从而可在保持原边界条件不变的情况下，一原电荷将原边界面移去。镜@=?一边界像电荷2025-6-112

2025-6-11 第二章 2.8 2 镜像法的实质是在待求场域的区域 以外,在适当的位置上人为地设置一些 点电荷或线电荷来等效原边界上复杂 分布的实际电荷对待求场域的作用.从 而可在保持原边界条件不变的情况下, 将原边界面移去. 镜像法的理论依据就是电磁场的唯一性定理.   ? 镜 原电荷 像电荷 边界

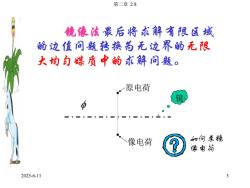
第二章2.8镜像法最后将求解有限区域的边值问题转换为无边界的无限大均匀媒质中的求解问题。原电荷d如何求镜像电荷?像电荷2025-6-11

2025-6-11 第二章 2.8 3 镜像法最后将求解有限区域 的边值问题转换为无边界的无限 大均匀媒质中的求解问题。  镜 原电荷 像电荷 如何求镜 像电荷

第二章2.8一、平面导体与点电荷1．无限大接地导体平面为z三O的平面，（xoy）平面，点电荷q距导体平面的距离为h，其周围是介电常数为%的介质，求介质中任意一点的场。P(x yz): qZ设置坐标系：h80导体z=O平面为导体平面，其参考电位为零。电位给定点电荷9与导体平面之间的电位满足：V2Φ=0z >0q所在点除外z=0Φ=02025-6-11

2025-6-11 第二章 2.8 4 一、平面导体与点电荷 1. 无限大接地导体平面为 的平面，（xoy） 平面，点电荷q距导体平面的距离为h，其周围是介 电常数为 的介质，求介质中任意一点的场。 z  0 0  q  0 h P(x y z) 导体 v 设置坐标系： z  0 平面为导体平面，其参考电位为零。 v 点电荷 q与导体平面之间的电位满足： z ＞0 0 2    q所在点除外 z  0   0 Z 电位 给定

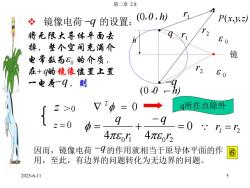
第二章2.8r*镜像电荷-q的设置：(0,0,h)P(x,y,z)a将无限大导体平面去60n掉，整个空间充满介镜电常数为% 的介质,12在+ g的镜像位置上置60一电荷-q，则(0.0 ,q所在点除外?=0z>0qa2=0=0 r=r14元4元82因而，镜像电荷一9的作用就相当于原导体平面的作6用，至此，有边界的问题转化为无边界的问题。52025-6-11

2025-6-11 第二章 2.8 5 v 镜像电荷 q 的设置： 1r h q 0  P(x y z) 镜 q 2 r (0，0，h) ， ， ， 0  将无限大导体平面去 掉，整个空间充满介 电常数为 的介质， 在 的镜像位置上置 一电荷 ，则 0   q q z ＞0 0 2    q所在点除外 z  0 0 4 4 0 1 0 2     r q r q    因而，镜像电荷 的作用就相当于原导体平面的作 用，至此，有边界的问题转化为无边界的问题。 q 6 2 r r  1  1r 2 r (0 0  h)

第二章2.8(0 0 h)P(xyz)C*求解：h60镜当z>0，任意一点P（xz）电位为：60q-q(0,0 ,-h)即d4元04元0°211q4元[++(2-h[2++(2+z=0，=Φ=0当 =0当z<0导体空间内,由于实际上无场源存在,故Φ42025-6-116

2025-6-11 第二章 2.8 6 1r h q 0  P(x y z) 镜 q 2r ， (0 ， 0 ， h) 0 当  z ＞0 ，任意一点 P ( x y z) 电位为： 4 0 1 4 0 2r q r q       即                     2 1 2 2 2 2 1 2 2 2 0 ( ) 1 ( ) 1 4 x y z h x y z h q   v 求解： 4 当 z  0 ， r  r   0 1 2 当 z ＜0导体空间内,由于实际上无场源存在,故   0 (0 , 0 ,  h)

第二章2.8导体平面上的感应电荷面密度P，=？Xq由边界条件：在乙=0边界上P(x yz)801hDin -D2n = Ps导体adaΦ2即 2Φ2 = 0ps&82anan11q.4元[x?+y? +(z-h)[? +y?+(2+h)2adad亦即p,=8080anaz1z=(qh.2元(x? + y? + h2)%2025-6-11

2025-6-11 第二章 2.8 7 v 导体平面上的感应电荷面密度  ?  s D1 n  D 2 n   s 由边界条件：在 z  0边界上 s n n             2 2 1 1 即 ∴ 2 3 2 2 2 2 ( x y h ) qh s        2  0 亦即 0 1 0 1 0          z s n z                          2 1 2 2 2 2 1 2 2 2 0 1 ( ) 1 ( ) 1 4 x y z h x y z h q   q  0 h P(x y z) 导体 1 2

第二章2.8xoy平面drds导体平面上的总感应电荷Q：dp采用极坐标系。=x+yds = dr . rdp如图：qhX0PsE2元(x2 + 2 + h2)rdrd pqh(0 0 h)P(xyz)222元q0(r? +h?)60镜qh即Q=80-q(r2 + h?) /2(0,0,-h)由上述分析可知：可将无限大接地导体平面视为一面镜子，其像电荷只有一个，就是原电荷的虚像，具与等值异号。2025-6-118

2025-6-11 第二章 2.8 8 v 导体平面上的总感应电荷Q： 采用极坐标系. 2 2 2 r x y o ds P(r  ) x y  d  r dr 如图: ds  dr rd         0 2 0 2 3 2 2 ( ) 2     r h qh rdrd Q ds s s 即 q r h qh Q      0 2 1 2 2 ( ) 由上述分析可知:可将无限大接地导体平 面视为一面镜子,其像电荷只有一个， 就是原电荷的虚像,且与q等值异号. xoy 平面 2 3 2 2 2 2 ( x y h ) qh s       1r h q 0  P(x y z) 镜 q 2 r ， (0 ， 0 ， h) 0  (0 , 0 ,  h)

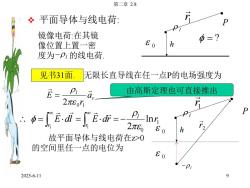
第二章2.8r平面导体与线电荷：XP镜像电荷:在其镜Φ=?80h像位置上置一密度为-Pi的线电荷见书31面无限长直导线在任一点P的电场强度为由高斯定理也可直接推出PiEa2元80rPE.dlH.Inr2元80r60h故平面导体与线电荷在z>0的空间里任一点的电位为60-Pi92025-6-11

2025-6-11 第二章 2.8 9 v 平面导体与线电荷: 镜像电荷:在其镜 像位置上置一密 度为 l 的线电荷.  0 h  l P 1r  2 r  l 0   0 h P  l 1r  见书31面. 无限长直导线在任一点P的电场强度为 r l a r E   2 0 1    1 0 ln 1 1 2 E dl E dr r l r r                   故平面导体与线电荷在z>0 的空间里任一点的电位为 由高斯定理也可直接推出   ?

第二章2.8P1Pilnr.)blnr +(2元802元80PiPiInr2Inr2元02元0见书2-67式pr2 元r20rPp1Φ=?80hV60Pl102025-6-11

2025-6-11 第二章 2.8 10 ln ) 2 ln ( 2 2 0 1 0 r r l l           2 1 0 ln 2 r r l     2 0 1 0 ln 2 ln 2 r r l l         见书2-67式  0 h  l P 1r  2 r  l 0    ?