《电磁场与电磁能》课程PPT教学课件(马冰然版)第七章 平面电磁波

第七章一5第七章平面电磁波电磁波:时变电磁场在媒质中以速度向远处传播。a平面电磁波:波前面(等相位面)是平面的波。2025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 1 第七章 平面电磁波 电磁波:时变电磁场在媒质中以速度 1 v = 向远处传播。 平面电磁波:波前面(等相位面)是 平面的波

第七章C7.1波动方程一、非齐次波动方程:在均匀、线性、各向同性媒质中,由麦氏方程导出:?E(r,t)aj(r,t)l?E(r,t)-μVp(r,t)at?atC(7-1-1)?H(r,t)?(r,t)-μ8-V×J(r,t)at?其中,EH一般情况下,有三个分量,且每个分量都可以是三维坐标变量及时间t的函数.即E=aE(x, y,z,t)+a,E,(x, y,z,t)+a,E,(x, y,z,t)2025/6/112电磁理论
电磁场理论 2025/6/11 第七章 2 7.1 波动方程 一、非齐次波动方程: 在均匀、线性、各向同性媒质中,由麦氏方程导出: ( , ) ( , ) ( , ) 1 ( , ) 2 2 2 r t t J r t t E r t E r t + = − 2 2 2 ( , ) ( , ) ( , ) H r t H r t J r t t − = − (7-1-1) 其中, 一般情况下,有三个分量,且每个分量都可以 是三维坐标变量 及时间 t 的函数. 即 E H . r E a E (x, y,z,t) a E (x, y,z,t) a E (x, y,z,t) x x y y z z = + +

第七章福二、齐次波动方程:5若考虑无源理想介质--------自由空间,则j=0p=0α=0故非齐次波动方程(7-1-1)齐次波动方程?E(r,t))=0?E(r,t)- μcat?(7-1-2)"H(r,t)8?H(r,t)-μe=05at?其中: B=a,E(x,y,z,t)+a,E,(x,y,z,t)+a,E(x,y,z,t)H=a,H,(x,y,z,t)+a,H,(x, y,z,t)+a,H,(x, y,z,t)32025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 3 二、齐次波动方程: 若考虑无源理想介质-自由空间,则 J = 0 = 0 = 0 故非齐次波动方程(7-1-1) 齐次波动方程 0 ( , ) ( , ) 2 2 2 = − t E r t E r t 0 ( , ) ( , ) 2 2 2 = − t H r t H r t (7-1-2) E a E (x, y,z,t) a E (x, y,z,t) a E (x, y,z,t) x x y y z z 其中 = + + : H a H (x, y,z,t) a H (x, y,z,t) a H (x, y,z,t) x x y y z z = + + 5 8

第七章C三、齐次亥姆霍兹方程.若时变电磁场为时谐(变)电磁场:则E(r,t) = Em(r)cos(ot + Pe)复有效值= Re[Em(r)ejpe -ejor量= Re| Em(r)ejot= Rel V2 E(r)ejot简记为: E(r,t) = ~2 E(r,t)ejol → E(r)ejalH(r,t) = V2 H(r,t)ejot =→ H(r)ejoat同理:2025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 4 三、齐次亥姆霍兹方程 若时变电磁场为时谐 (变)电磁场:则 = = = = + • • j t j t m j j t m m e Re 2 E r e E r e E r e e E r t E r t e ( ) Re ( ) Re ( ) ( , ) ( ) cos( ) 简记为: j t j t E r t E r t e E r e ( , ) 2 ( , ) ( ) • • = 同理: j t j t H r t H r t e H r e ( , ) 2 ( , ) ( ) • • = 复有 效值 矢量

第七章则齐次波动方程的场量以复数形式代入时为3V2 E(r)-(jo) μuc E(r)=0V? H(r)-(jo) μc H(r) = 0时谐场齐次波动方程V? E(F)+ k2 E() = 0(7-1-3)? ()+k? () = 00?其中:2=时间变量已消去二o2025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 5 则齐次波动方程的场量以复数形式代入时为: ( ) ( ) 0 2 2 + = • • E r k E r ( ) ( ) 0 2 2 + = • • H r k H r (7-1-3) 其中: 2 2 2 2 v k = = 时间变量已消去. 3 ( ) ( ) ( ) 0 2 2 − = • • E r j E r ( ) ( ) ( ) 0 2 2 − = • • H r j H r 时谐场齐次波动方程

第七章7.2理想介质中的均匀平面波理想介质中的均匀平面波:=0电、磁1、均匀平面波:波前平面场量振幅处处相等。2、沿Z轴方向传播的均匀平面波:E(r,t)=aE,(x, y,z,t)+a,E,(x, y,z,t)+aE.(x, y,z,t)设时刻t=ti,波前面位于 z=z,则E(r,t)=a,E,(x,y,z1,t)+a,E,(x, y,z1,t)+a,E.(x, y,21,t)62025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 6 7.2 理想介质中的均匀平面波 一、理想介质中的均匀平面波: = 0 1、均匀平面波: 波前平面场量振幅处处相等。 电、磁 2、沿 z 轴方向传播的均匀平面波: E(r,t) a E (x, y,z,t) a E (x, y,z,t) a E (x, y,z,t) x x y y z z = + + 设时刻 t = t 1 ,波前面位于 1 z = z ,则 ( , ) ( , , , ) ( , , , ) ( , , , ) 1 1 1 1 1 1 1 E r t a E x y z t a E x y z t a E x y z t x x y y z z = + +

第七章均匀平面波波前平面场量振幅处处相等。E(r,t)=a,E(z,t)+a,E,(z,t)+a,E,(z,t)故均匀平面波场量只是一维坐标变量 Z 与时间t的函数。即E(r,t) = E(z,t)(7-2-1)H(r,t) = H(z,t)2025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 7 ∵ 均匀平面波波前平面场量振幅处处相等。 ( , ) ( , ) ( , ) 1 1 1 1 1 1 1 E(r,t ) a E z t a E z t a E z t x x y y z z = + + 故均匀平面波场量只是一维坐标变量 与时间 的函数。即 z t E(r,t) E(z,t) = H(r,t) H(z,t) = (7-2-1) 9

第七章C3、均匀平面波(Z方向传播)的齐次波动方程A将(7-2-1)代入(7-1-2)有:3?E(z,t)1 ?E(z,t):0o2Oz?at?(7-2-2)1 α?H(z,t)α?H(z,t)102oz?at?其中E(z,t)=a,E.(z,t)+a,E,(z,t)+a.E.(z,t)三个标量方程H(z,t)=a,H,(z,t)+a,H,(z,t)+a,H,(z,t)82025/6/11电磁巧理论
电磁场理论 2025/6/11 第七章 8 3、均匀平面波( z 方向传播)的齐次波动方程: 将 (7-2-1) 代入 (7-1-2) 有: 0 ( , ) 1 ( , ) 2 2 2 2 2 = − t E z t z E z t v (7-2-2) 其中: E(z,t) a E (z,t) a E (z,t) a E (z,t) x x y y z z = + + H(z,t) a H (z,t) a H (z,t) a H (z,t) x x y y z z = + + 3 三个标量方程 11 2 2 2 2 2 ( , ) 1 ( , ) 0 H z t H z t z t − = v
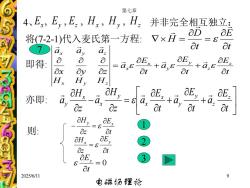
第七章1HH.EE..H.H并非完全相互独立:x1aEaDVxH一方程:将(7-2-1)代入麦氏第Catata.axayaE,aaaaEaE.即得:1ax8COzaxOyatatOtHxH.HaHOEaEaE,aH.亦即:aaaaCaOzatatOzatoH,aE,则:atOzaE,aHOzatOE.:0Cat2025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 9 4、 Ex , Ey , Ez , Hx , Hy , Hz 并非完全相互独立: 将(7-2-1)代入麦氏第一方程: t E t D H = = 即得: t E a t E a t E a H H H x y z a a a z z y y x x x y z x y z + + = 亦即: + + = − t E a t E a t E a z H a z H a z z y y x x y x x y 则: t E z Hy x = − t E z Hx y = = 0 t Ez 1 2 3 7

第七章同理:将(7-2-1)代入麦氏第二方程:得aE,aH.OzataH,aExatOz13aH.= 0at分析:A1)由若不计对时间 t为恒定的分量,则36纵向H,(z,t) =0E,(z,t)= 0其物理意义为:电场、磁场均无平行传播方向的分量横电磁波2025/6/11电磁场理论
电磁场理论 2025/6/11 第七章 10 同理:将(7-2-1)代入麦氏第二方程:得 t H z Ey x = − − t H z Ex y = − = 0 − t Hz 4 5 6 分析: 1) 由 3 、6 若不计对时间 t 为恒定的分量,则: E (z,t) = 0 H (z,t) = 0 z z 其物理意义为:电场、磁场均无平行传播方向的分量。 13 纵向 横电磁波
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)总结复习.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第六章 时变电磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第一章 静电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第二章 恒定电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第三章 恒定磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第四章 时变电磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第六章 平面电磁波的传播.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第五章 准静态静电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第七章 均匀传输导线中的导行电磁波.ppt
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第1章 自由空间中的麦克斯韦积分定律.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)目录.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第5章 根据边值观点的电准静态场.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第2章 自由空间中的麦克斯韦微分定律.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第6章 极化.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第3章 准静电学与准静磁学导言.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第4章 电准静态场 重叠积分观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第7章 传导与电准静态的电荷弛豫.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第9章 磁化.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第8章 磁准静态场 重叠积分和边值观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第10章 磁准静态弛豫和扩散.pdf
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)复习题题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第五章 静态场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第三章 恒定电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.10 静电场能量、静电力.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.9 导体系统的电容.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.7 唯一性定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第四章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.6 分界面上的边界条件.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.8 镜像法.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.5 泊松方程和拉普拉斯方程.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.4 高斯通量定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.3 静电 场中的导体与电介质.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.1 库仑定律与电场强度 2.2 电位.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第二章 静电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第三章 静电场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第四章 恒定电流场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第五章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第六章 电磁感应.ppt
