《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第6章 极化

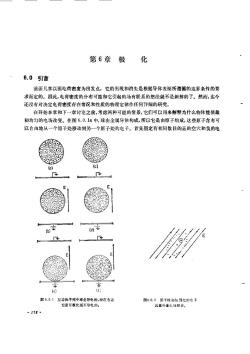
化第6章极6.0引言前面几章以面电荷密度为出发点，它的出现和消失是根据导体表面所遵循的边界条件的要求而定的。因此，电荷密度的分布可能和它引起的场有联系的想法就不是新鲜的了。然而，迄今还没有对决定电荷密度存在情况和性质的物理定律作任何详细的研究。在开始本章和下一章讨论之前，考虑两种可能的情景，它们可以用来解释为什么物体能使最初均勾的电场改变。在图6.0.1a中，球由金属导体构成，所以它是由原子组成，这些原子含有可以自由地从一个原子处移动到另一个原子处的电子。首先假定有相同数目的正的空穴和负的电(c)b图6.0.1左边的序列中球是导电的，而在右边图6.0.2原核和包俩它的电子居可极化面不街白云靠外施电场移位。158

子。在没在外加场以及在尺度比原子川的距离为大(即在宏观尺度)的情况下，在物质内部任一点都没有电荷密度。当这个物体放入原先均勾的电场中时，电子受到力的作用，此力企图使它们集中到球的南极。这只要求电子稍微向下移动(平均说来，小于原子间的距离)。因为在最终的平衡(稳定)状态,球的内部必须没有电场,所以在材料体积内各点电荷密度保持为零。但是,要维持净电荷为零，球北极原子正的位置是暴露的。过了一些时间,净结果是示于图 6.0.1b的面电荷密度分布。[事实上，如果电极远离球体，这就是例5.9.1中求得的分布。1现在考虑另一种物理情景，它能导致非常相似的结果。如图6.0.1c所示，材料由原子、分子或分子团（电畴）组成，在材料中电场感生偶极矩。例如，假设偶极短有原子的尺度，并且在没有电场时它不存在；偶极矩被感生是因为原子包含带正电的原子核以及沿着轨道绕原子核旋转的电子。按照量子理论，沿轨道绕原子核旋转的电子在任何特定瞬间不能看成是固定的。把电子设想成包围原子核的电荷“云"更为合适。由于沿轨道旋转的电子的电荷与原子核的电荷等量异号，中性的原子没有净电荷。不具有永久偶极矩的原子还有另外的性质，它的电子"云"的负电荷的中心与原子核的正电荷的中心重合。存在电场的情况下,正电荷的中心被拉向场的方向,而负电荷的中心被推向相反的方向。在原子范围，这一电荷中心的相对位移如图 6.0.2中所示。由于两个电荷的中心不再重合，粒子获得偶极矩。这样，我们可以用一对量值相等、符号相反，间距为&的电荷表示每个原子。在外施场内，在球体的宏观尺度上，出现偶极子，有点象图6.0.1d所示。在球的内部，极化使每个正电荷留在负电荷的附近，从而没有净电荷密度。但是在北极没有负电荷去中和正电荷，并且在南极没有正电荷与负电荷配对。结果就有面电荷密度分布,性质上与金属球情况下的结果没有差别。我们怎样能够区别这两种非常不同的情况：假设这两个球体都与下电极接触，如图中的(e)和(1)所示。这样做，我们的意思是在金属球的情况下，电子可自由地通过球与电极之间。电子仍旧是稍微向下移动，留下正的位置暴露在球的顶部。然而，有一些在底部的电子流入下电极，从而减少了在金属球下方负的面电荷的数量。在顶部，图6.0.1f 所示的极化了的球有类似的正的面电荷密度分布。但是这两种情况有一非常重要的差别是显而易见的。在理想电介质内，在原子尺度上沿轨道的电子与原来的原子是成对的，所以球一定保持中性。这样，金属球现在带有净电荷，而由偶极子组成的球没有净电荷。实验证明金属球确实获得了净电荷，它可以用一些不同的方法得到。其中两个从第1章的演示清楚地显示出来。对球体各通过“感应”的方式带电，将会相互推斥，这可由图1.3.10的实验显示。电荷也能根据电荷守恒进行测量，如演示1.5.1中那样。推测起来，用绝缘球进行同样的实验能够表明不存在净电荷。因为电荷的积聚是通过成对电荷的位移(极化)以及通过能够远离有相反符号的配对电荷的位移发生的，因此用把总电荷密度p分成p。和p，两部分，来区分这两部分电荷往往是合适的，Pu和P,分别由不成对的和成对的电荷产生。.159

(1)=pa+pp本章中考虑绝缘材料，所以集中注意成对的或极化电荷密度的作用。不成对电荷的额外的作用在下章中讨论。在6.1节中，我们第一步是建立极化电荷密度与偶极子强度一一极化强度*的关系。我们这样做是因为极化强度很容易确定。然后在 6.2和6.3两节注意两个一般的极化种类中的第一类。在这几节中，极化强度是永久的，所以确定时不考虑电场。在6.4节我们讨论表示场对极化的作用的简单构成定律。这种刚描述的由场感生的原子极化，是典型的物理情况。场对原子、分子或电畴的作用伴随有偶极子对场的反作用，必须同时考虑。即置于电场中的这种可极化物体的内部，产生极化电荷密度，反过来，它又改变了电场。在6.5—6.7诸节我们将学习一些方法，通过它们来获得这种问题的自相一致的解答。6.1极化强度下面的推导过程适用于具有各种微观起源的极化现象。无论代表的是原子、分子、有序的原子或分子团（电畴)，或者甚至是宏观粒子、偶极子被描绘成相反的两个电荷士用矢量距离d分开，其方向从负电倚到正电荷。因此，单个偶极子，如4.4节所表示的，它的偶极矩P定义为p=qd(l)因为d的量值一般小于原子、分子或其他粒子的尺寸，所以它比所关心的任何宏观尺寸为小。现在考虑媒质由每单位体积N个这种极化粒子组成。在由面S包围的任意体积V内包含的净电荷是多少？显然，如果在V内媒质的粒子是未极化的，在V内的净电荷就是零。但是，现在它们是极化的，有些电荷在未极化状态时，中心包含在V内，现在移到面S的外面，而在里面留下未中和的电荷中心。要确定留在√内的净的未中和电荷，我们假设(不失一般性)在极化过程中电荷的负中心是不动的，只有电荷的正中心是可移动的。考虑图6.1.1所示在面S上面元da附近的d粒子。现在在S外面，体积de=d·da内的全部美推王的电荷正中心，都留下了负电荷中心。这些对V提供了净的负电荷。由于在dp内存在Nd·da个这种负电荷中心，留在V内的净电荷为(2)1Q=-f(aNd).da图6.1.1 含有正电荷的体积元,它将负电荷留在面8的另一边。E注意被积函数可以是正的或负的，取决于通过面元dα 的电荷的正中心是离开√还是进人V出现哪一种可能性与d和da的相对取向有关。如果d有一分量与da方向相同（机反)，则电荷的正中心通过dα离开（进人)V。式(2）的被积函数具有每单位休积偶极矩的量纲，因此被定义为极化强度：原文为极化密度，本书按我国的习惯译虑极化强度。后网。评者许。.160

(3)P=Nqd此外还根据定义，V内的净电荷可以由极化电荷密度对它的体积积分确定Q=f,pdo(4)这样，我们有两种计算净电荷的方法，第一种方法是在式(2)的面积分中利用式(3)的极化强度。-f v.Pdu(5)Q--$p.da--这里已利用高斯定理将面积分转换成对被包照体积的体积分。从这个体积分求得的电荷、定与第二种计算净电荷的方法，即用(4)式求得的结果相同。由于所考虑的体积是任意的，在式(4)和(5)的体积分中的被积函数一定相同。(6)p,=-v-P这样，极化电荷密度P，就与极化强度P相关。在此推导过程中似乎没有达到目的，因为代替未知量Pp，出现了新的未知显P。在有些情况下，P是已知的。但是即使在较为常见的情况下，极化强度从而极化电荷密度事先是未知的，而是由场感生的，把P与E直接联系起来比使p，与E联系要更容易些在图6.0.1中，极化球得不到净电荷。我们用极化强度表示极化电荷密度就保证这是正确的。要明白这点，假设√被理解为包含整个极化体的体积，使包围体积V的面S落在极化体的外面。因为在 S上的P为零,式(5)的面积分一定为零。通过式(6)与极化强度有关的任何电荷密度分布不能对绝缘体提供净电荷。我们往往发现需要用不连续函数表示极化强度。例如，在被自由空间包围的物质中，象图6.0. 1.中的球，极化强度在界面处能从-个有限值降为零。在这种区域中，可以有面极化电荷密度。怀着要从P确定此电荷密度的目的，式(6)可以对包围界而的增量面积的药丸盒积分。当进行-P→esE和 p>p的替代时,式(6)取与高斯定律相同的形式,所以证明过程与从式(1.3. 1)导出(1.3.17)是相同的。我们得出结论，在P的法向分量有跃变的地方，就有面极化电荷密度。(7)n.(P-P)G=-正如式(6）告诉我们在材料的体积内怎样对于已知P的分布确定极化电荷密度，这个表达式可用来计算在界面处极化电荷密度的奇异性（面极化电荷密度)。注意按照式(6)，P起源于负极化电荷而终止于正电荷。这与E和电荷密度间的关系相反。图6.,1. 2直圆柱体的均匀极化引起的极化面电荷。例如，按照(6)和(7)两式，示于图6.1.2中均勾极化的材料圆柱休，当P向上指时，在顶部有正0s，而负的在底部。161 :

6.2 存在极化时的定律与连续性条件当不成对的和极化的电荷密度区分开时，高斯定律变成(1)V'erE=pup,这里式(6.1.6)使p与P相关(2)P,--V.P因为P是每单位体积“平均"的极化量，它是在原子尺度上的位置的“平滑”失量函数。在这个意义上，它是一个宏观变量。它的散度的负值，即极化电荷密度，也是一个宏观量，它不反映微观电荷分布的“粒度”。这样，因为它出现在式(1)中，电场强度也是一个宏观变量。象获得式(1.3.7)那样,进行式(1)对包围界面的一部分的增量体积的积分,结果是(3)n·E(E*-Eb)=0.u+am这里式(6. 1.7)使0sp与P相关g,=-n. (Pa-Pb)(4)这最后的两个等式分别给出在不连续的表面上，高斯定律式(1)的连续性条件。极化电流密度与安培定律高斯定律不是受到极化影响的仪有的定律。如果极化强度随时间变化，则穿过6.1节中所述的面 S的电荷流动构成电流。因此我们需要研究电荷守恒,并且更一般地研究时变极化强度对安培定律的影响。为此，下面的步骤能导得用时变极化强度表示的极化电流密度。按照6.1节中得出的P的定义，极化过程中通过表面的面元da转移电荷量dQ?dQ=P.da这可以根据图6.2.1所示的体积d·da能大致预见。如果极化强度P随时间变化，则按照此等式，()K电荷以有限的速率通过面元。对于qNd或P变茅推王化AP,通过增量面元da的电荷最为A(dQ) =△P.da6)图6.2.1电荷通过面元da引起极化电流密度2注意在此表示式中我们有两个微分标记。 d表示Q是微分的这一事实，因为da 是微分。1dQ随时间的变化率，△(dQ)/At可以用电流di，表示，它从(b)这一边通过da到(a)这一边。di,-A(do)- P.da(7)A偏微分符号用来把对t的微分与P的空间依从关系区别开。通过面元da的电流di通常写成电流密度点乘da(8)di,=J,-da出此我们比较最后这两个式了，并导出极化电流密度是162

J.-号(9)注意J，和P，通过式(2)和(9)自动地服从连续性定律，它与电荷守恒方程(2.3.3)有相同的形式。J,+02=0(10)因此我们可以把在材料媒质中电荷转移的速率看作是由不成对电荷的也流密度J。和极化电流密度J，组成，各自服从它自已的守恒定律。这也是由安培定律稳含的，象现在这样推广到包括极化的效应。在EQS 近似法中，磁场强度一般不是所关心的，所以安培定律是次要的。但如果要确定H,J，就会作出贡献。这就是说，由式(2.6.2)所给出的安培定律现在将电流密度分成成对的和不成对的两部分来重写。当后者由式(9)给出时，推广到包括极化的安培微分定律是V×H=J.+%(eE+P)(11)无论是否作了准静态近似，这个定律都是有效的。但是，在EQS近似法中，一一般所关心的是电葡守恒的含意。这样,式(11)的散度在左边得零,考虑到式(1)、(2)和(9),表达式变成VJ.+e+ VJ,+e=0(12)因此，当时(11)式加上极化电流密度时，安培定律的散度给出极化电荷的守恒方程式(10)，和不成对电荷的守恒方程Ja+g=0(13) 之和。在本章的剩余部分,将假定在极化材料中,P一般为等。因此要到第7章中，（13)式才会起作用。位移通量密度在主要处理与场有关的极化现象时，一般把出现在高斯定律和安培定律中的物理量的组合，定义为位移通量密度D。t+3(14)D=FE+P我们把P看作是表示物质的，而把E看作是由外部的源引起的场量，并且源是在物质内。?这就提议D应被考虑成一个“混合"量。不是所有的电磁学教材都采取这个观点。我们把出现在麦克斯韦方程组中所有的量区分为场的量和物质的量，将有助于构筑场与物质相互作用的模新型。当p,用式(2)代替时，商斯定律(1)可以由式(14)定义的D写成(15)V.D=pu同时有关的连续性条件式(3)，当g.p用(4)代替时,变成· 163·

(16)n(D"-D)=GauD的散度和D在法向的跃变可确定不成对的电荷密度。在白由空间和物质中，式(15)和(16)不变形式，都成立。要使定律适合于自由空间，只要置D=e.E。安培定律也能方便地用 D表示。将式(14)代入(11),得VXH=J.+@D(17)现在位移电流密度aD/at中，包括了极化电流密度。6.3永久极化通常，极化取决于电场强度。，但是，在有些材料中，永久极化被“冻结”在材料中。理想情况，这意味着P(r，t）被规定为与E无关。用来制造话简和电话话筒的驻极体，往往用这种方式模拟当P是空间的、也许述是时间的给定函数时，极化电荷密度和极化面电荷密度分别可由式(6.2.2)和(6.2.4)得出。如果在整个材料中不成对的也御密度也给定，高斯定律中的总电荷密度和高斯定律的连续性条件中的面电荷密度就是已知量。[式(6.2.1)和(6.2.3）的右边已知。]这样，永久极化问题的摘述就可按照第4和5章中所用的相同的格式进行。本节中的例于试图得出对极化强度P,极化电荷密度p，和电场强度E之间的关系的评价。应该认识到一且P，从给定的P确定，第4和5章中的方法是直接可应用的。成对的和不成对的电荷问的区别有时是纯理论性的。使绝缘材料承受非常大的场，特别在高温下，可能追使分子或分于畴进人极化状态，并能在较低的场和温度下维持一段时间。把这看成是永久极化状态是很自然的。但是，如果离子被用来碰撞材料的表面，它们能够形成永久电荷的位置，当然，这些离了的起源使人想到它们可被看作是不成对的。然而如果材料吸引其他电荷而变成中性的，象它试图做的，这些永久电荷也能被看成是由于极化造成的，并用永久极化电荷密度表示在本节中，EQS定律占优势。这样，如果在整个所关心的区域内（不包括包留的边界：电荷密度都给定，E=-v0(1)V=-(pu+pp)(2)现在要考虑类似于图6.1.2中定性地描绘的那个例子。通过把均匀极化材料制作成球形的办法，可能获得场的分布的简单解答。例6.3.1永久极化球一-半径为R的材料球沿2轴均勾极化，(3.PPt.+ 164

给定周围的区战是白由空间，没有附加的场源，由这个永久极化产生的电场强度E是什么？布。在体积内，P的负散度为零，所以没行体极化电尚一步是在材料体积内和它的表面上确定P，的分不密度，见式（6.2.2)。当P用笛卡儿坐标系书写时，这是明显的，用球坐标分量表示时，就不大明显4P-Pocosdi,-Pasinfi,P的法向分量的突变需要极化面电荷密度。这些是用式(4)在T=R处计算(6.2.4)式的连续性条件得出的，该处法向分量是i,，且区域(a)是在球的外面。(5)Oan-P.coat这个面电荷密度产生E。既然场源已经确定，情况问复到很象习题5.9.2 所说明的那样。在内和在周围的自由空间内，电位都必颈满足拉普拉期方程，即Pa+0,-0时的式(2)。在r=RB处由式(1)和(2)隐含的连续性条件［式（5.3.3）和(6.2.3)了，如用史表示，用式(5)计算后者时，是(6)@(7)-+-Pcoso式中上标(0)和(i)分别表示球外和球内区）由这个电位所表示的E场的源是随θ作余弦变化的百极化电荷密度。如果拉普拉斯方程的两个球坐标解答(根据5.9节)具有与的依从关系是cose,满足边界条件式(6)和(7)能的。由于球外区域没有源，所以当 r→时,电位必须趋于零。有 cos 相关性的两个可能的解答中,偶极子场用于球的外部。00=ACOs(8)在球的内部,电位必须是有限的,因此这个解答排除在外。解答是(9)i-Brcog它是均匀电场强度的电仪。将这些表达式代人违续性条件式(6)和(7),得到的表达式可以提出公因子 coag。这样，在面上的每一点能满足近界条件，如果(10)A-BR-0(11)20A+o=P.由这两个表达式可解出4和B，把它们引入式（8）和（9）可得出电位分布0-Pa e(12)(13)EIn51a-rcosi最后，取此电位的负梯度，就得到所要求的电场分布E-PR(20i,+ sino01)(14)2Paa(15)EI-( costi,+sindia)茶当极化强度的分布如插图所示时，图6.3.1表示这个电场强度。E线起翁于正电荷利终止于负电荷不是意外的。极化强度起始于负极化也荷和终,旺于正极化电荷。致后得到的电场是典型的，因为在球的外部恰好是位于原点的偶极子的电场，而在球的内部是均匀场。下原点的偶极了，产压和均句极化球的外部用周的电场，其极矩是什么！这可以从化较（12)租（4.4.10)两式看出。155

(16)IP-→tRP.偶极矩筒单地就是体积乘以均勾极化强度在下一个例子中有两个新的要点。第一，所关心的区域的边界上电位是受约束的。第二，给定的极化强度描述极化电荷密度的体分布而不是面分布。例 6. 3. 2 具有给定边界条件的体极化电荷引起的场在平面3=士α内的平行平面电极被约束处于零电位。在电极间的乎面区域内，极化强度是空间的周期函数P=-ifgsin p2(17)我们希望确定场的分布。"图 6. 3. 1 具有均匀极化强度的永久极化腺的等位线和电场强度线。插图示出极化强度和相关的询极化电荷密度首先，通过取(17)的负散度[把(17)式代入(6.1.6)式了确定极化电荷密度的分布(18)Op=pocosBa所求得的极化强度和极化电荷密度的分布示于图 6. 3. 2(Po<0)。现在情况间复到求解拍松方程,给定这个额分布,并且在 3一±4 的边界上服从举电位条件。这个问题和例5,6.1中所考虑的相同。电位和场都是图5.6.2中措述的特解和齐次解的登加。一个例子说明永久极化如何与机械变形一起产生有用的电信号。E图6.8.2周期分布的极化强度和相关的极化电待临度图6.3.3驻极体话简的横截面P<0）产生图5.6.2所示的电位和场。例 6, 3. 3胜极体话图6.3.3中示街的核截面是厚度为4的永久极化材料凝片。它的下面由电位为的周定电极界定，上面由空气隙界定。在此气隙的另一边是导电的接地膜，它作为话伤的可动充作。它被安装在支架上以便经受位移。这样，间隙为二h(1)。如已知为(t),在负载电阻R两端得到的电压是什么！在片中，极化强度是均勾的，最值为P，方向从下电极指上也极。这个欠龄没有散度，所以式(6.1.6)的￥166

计算表明在片的体积内，极化电荷密度为零。在驻极体空气隙界上的极化尚电荷潮度，可从(6.1.7)式得剂为P-Pn因为α，是均的，并且等电位边界是平行平面的，空气赋[区域（a)1中和驻极体[区域(b)中的电场都可看成是均勾的。E=i, R; dn。在空气中，电摄上不成对电荷引起的场加强了口引起的汤，而在驻极体中，它反对0引起的指向向下的场为了计算图6.3.3中规定的电流，下电极和驻极体用一表面9包面，并且应用高斯定律来计算被包国的不感对电荷。V.(eE+P)=p,-d (e,E- P).nde(25)葡S究竟么样切过系统，无类聚要。这里我们把面取威通过（随包围下电极。从式(24),可衍不成对电荷是1=Aof-e(0+aP(26)式中4是电极的面积不成对电荷的守恒要求电流等于在下电极上总的不成对电荷的变化率=%(27)当电阻器连接到端钮上时（由话简激动的放大器的输入电阻，电压和电流还必须满足欲姆定律(28)最后这三个关系式结合在一起,在h(0)给定时,可得出 D(t)的表达式。--(+a+4%(29)1E-7logcPLW-/RC.cge(6)图6.8.4（a驻极体话简中极化强度和面电荷密度的分布，图6.3.5施加膜位移的驻极体话简的顾率购应)电场强度和面锻化电补以及不成对的电荷。+167