西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第七章 均匀传输导线中的导行电磁波
第7章均匀传输线中的导行电磁波 7.0序 7.1无损耗均匀传输线方程 7.2无损耗均匀传输线的传播特性 7.3无损耗传输线中波的反射和透射 7.4无损耗传输线的入端阻抗 7.5无损耗均匀传输线的阻抗匹配 7.6有损耗均匀传输线
第 7 章 均匀传输线中的导行电磁波
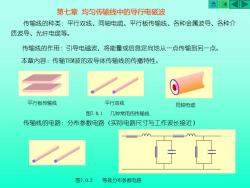
AKKD第七章均匀传输线中的导行电磁波传输线的种类:平行双线、同轴电缆、平行板传输线、各种金属波导、各种介质波导、光纤电缆等。传输线的作用:引导电磁波,将能量或信息定向地从一点传输到另一点。本章内容:传输TEM波的双导体传输线的传播特性。平行板传输线平行双线同轴电缆图7.0.1几种常用的传输线传输线的电路:分布参数电路(实际电路尺寸与工作波长接近)VV图7.0.2等效分布参数电路
第七章 均匀传输线中的导行电磁波 传输线的种类:平行双线、同轴电缆、平行板传输线、各种金属波导、各种介 质波导、光纤电缆等。 传输线的作用:引导电磁波,将能量或信息定向地从一点传输到另一点。 本章内容:传输TEM波的双导体传输线的传播特性。 平行板传输线 平行双线 同轴电缆 图7.0.1 几种常用的传输线 传输线的电路:分布参数电路(实际电路尺寸与工作波长接近) 图7.0.2 等效分布参数电路

合KD7.1无损耗均匀传输线方程假设传输线均匀且无损耗,传播TEM波。Zi=0结点电流方程aidzi +LodzazaiaaOudz)dz+C,dzi=i+(u+azatOz(z,t)+Xaudz.....Codzu(z,t)u+az回路电压方程Zu=0aiauu= Ldzdz+u+图7.1.1均匀传输线电路模型atOz同除以dz,略去二阶无穷小项(dz)2,得传输线方程i+couu+L.oOFLOtoatO-进一步整理。得电压u,电流i的波动方程a'i-lai'uoulou=LC.0%=LC.OCavarwatO2"at1式中v传播速度,L、C。分别为传输线单位长度的电感及电容二VL.C
7.1 无损耗均匀传输线方程 假设传输线均匀且无损耗,传播TEM波。 结点电流方程 i = 0 dz) z u ( u t dz C dz z i i i 0 + + = + 回路电压方程 u = 0 dz z u u t i u L dz 0 + + = 同除以dz,略去二阶无穷小项(dz) 2,得传输线方程 0 t u C z i 0 = + 0 t i L z u 0 = + 图7.1.1 均匀传输线电路模型 进一步整理。得电压u,电流 i 的波动方程 2 2 2 2 2 2 0 0 2 t u v 1 t u L C z u = = 2 2 2 2 2 2 0 0 2 t i v 1 t i L C z i = = 式中 —— 传播速度, 分别为传输线单位长度的电感及电容 L0C0 1 v = L0、C0

ANKD7.2无损耗均匀传输线的传播特性7.2.1瞬态解a'u'uu(zt)=u(t-三)+u(t+二)波动方程=L,C,波动方程的解ata22oiaii(2,t)=t(t-三)+t(t+三)=L.CoarO1分别称为入射电压波、电流波:反射电压波、电流波。7.2.2正弦稳态解dd'u=(jo)LCU=ku=(jo)LCi=kidz?dz?式中k=iB=jo/Lc相位常数传播常数:β=OVLC方程的解U(=)=te-i+U-ea1i(z)=ite-准+ie-作=(Ue-i-U-e)Z.式中Zo特性阻抗U+U-Lo2Z. =(实数)itiVC
7.2 无损耗均匀传输线的传播特性 7.2.1 瞬态解 波动方程的解 ) v z ) u (t v z u( z,t ) = u (t − + + + − ) v z ) i (t v z i( z,t ) = i (t − + + + − 分别称为入射电压波、电流波;反射电压波、电流波。 7.2.2 正弦稳态解 ( j ) L C I k I dz d I ( j ) L C U k U , dz d U 2 0 0 2 2 2 2 0 0 2 2 2 = = = = 式中 k = j = j L0C0 ——传播常数; = L0C0 ——相位常数 方程的解 j z j z U( z ) U e U e + − − = + (U e U e ) Z 1 I( z) I e I e j z j z 0 + − jz − − jz + − − = + = − 式中 Z0 ——特性阻抗 = = − − = − + + 0 0 0 C L I U I U Z (实数) 波动方程 2 2 2 0 0 2 t u L C z u = 2 2 2 0 0 2 t i L C z i =

AKKD1. 已知始端电压 亡,和电流I,(z=-l)将已知条件代入通解i+0=i+U-iUU,Z11-(-0")a解得复常数为ozUt=-(u,+zie-inU-=,(U,-Z,i,Jejm图7.2.1已知ui的传输线2代入通解,得U(2)=(U,+Z,1, )e-8(42) +号(U,-Z.i,Je(z)++i,Je-p(+2) -iJeB(I+z)i(=)=一利用欧拉公式,得U(=)=U,cos β(l+z)-jZ,i, sinβ(l+=)i(=)=i,cos β(1+=)-jsinB(l+=)Z.z0注意:
1. 已知始端电压 U 1 和电流 I ( z l ) 1 = − 将已知条件代入通解 j l j l U1 U e U + − = + (U e U e ) Z 1 I j l j l 0 1 + − − = − 解得复常数为 j l 1 0 1 (U Z I )e 2 1 U + − = + j l 1 0 1 (U Z I )e 2 1 U = − − 利用欧拉公式,得 U(z) U cos (l z) jZ I sin (l z) = 1 + − 0 1 + sin (l z ) Z U I( z ) I cos (l z ) j 0 1 = 1 + − + 注意: z 0 , l 0 代入通解,得 j ( l Z ) 1 0 1 j ( l Z ) 1 0 1 (U Z I )e 2 1 (U Z I )e 2 1 U( z ) − + + = + + − j ( l Z ) 1 0 j ( l Z ) 1 1 0 1 I )e Z U ( 2 1 I )e Z U ( 2 1 I( z ) − + + = + − − 图7.2.1 已知 U 1 ,I 1 的传输线

ANKD2.已知终端电压U,和电流i(z=0)将已知条件代入通解(U-u-)U,=0*+0-1Le+解得复常数为UU1Ut==(U,+z.i,)2C(0,-Z.J.)U-=-Z02图7.2.2已知0,的传输线代入通解,整理后,得Ui(z)=1,cos sinβzU(=)=U,cosβz-jz,i,sinβ一Z.3.传输线的有功功率P=R(ui*=(U+e-it+U-ejt)(itejt+i-e-p)=R(U+it+U+i-e-12 +U-itej2p +U-1-)仅有虚部=(0-0-0/z传输功率等于入射波功率减去反射波功率
2. 已知终端电压 U 2 和电流 I ( z 0 ) 2 = 将已知条件代入通解 + − U 2 =U +U (U U ) Z 1 I 0 2 + − = − 解得复常数为 (U Z I ) 2 1 U 2 0 2 = + + (U Z I ) 2 1 U 2 0 2 = − − 代入通解,整理后,得 U(z) U cos z jZ I sin z = 2 − 0 2 sin z Z U I( z ) I cos z j 0 2 2 = − 3. 传输线的有功功率 传输功率等于入射波功率减去反射波功率 P R (UI ) (U e U e )( I e I e ) j z j z j z j z e + − − + − − = = + + R (U I U I e U I e U I ) j2 z j2 z e + + + − − − + − − = + + + 0 2 2 ( U U )/ Z + − = − 仅有虚部 图7.2.2 已知 U 2, I 2 的传输线

AKKD7.3无损耗传输线中波的反射和透射7.3.1反射系数和透射系数负载端反射系数1.负载端电压、电流分别为ZtU(0)=U*+U和i(0)=(U+-U-)/Z负载阻抗07U++U-1+U-/U+U(0)1v=ZoU+-U-01-U-/U+i(0)图7.3.1不均匀传输线(复数)反射系数U+Z+Zo2.沿线任一点反射系数U-ejpUitriePa=[1ler准m (r是的丽数)厂Ute-JfU++U3..不均匀传输线的反射系数Zo1Zo2U-Z=0处U*+0-=U"U01I++- =(U+-0-)/Z,=I=Z.UZ-Zo图7:3.2不均匀传输线I,=解得,反射系数U+Z.+Z.(Z等效于Z,)
7.3 无损耗传输线中波的反射和透射 7.3.1 反射系数和透射系数 1. 负载端反射系数 负载端电压、电流分别为 + − U (0 ) =U +U 和 I(0 ) (U U )/ Z + − = − 负载阻抗 − + − + + − + − − + = − + = = 1 U /U 1 U /U Z U U U U Z I(0 ) U(0 ) ZL 0 0 反射系数 L i L L 0 L 0 L e Z Z Z Z U U = + − = = + − (复数) 2. 沿线任一点反射系数 3. 不均匀传输线的反射系数 解得,反射系数 02 01 02 01 L Z Z Z Z U U + − = = + − j( 2 z ) L j2 z j z j z z L e e U U U e U e + + − + − − = = = ( z ) z是 的函数 U +U =U + − 02 01 Z U I I (U U )/ Z I + = − = = + − + − Z=0处 图7.3.1 不均匀传输线 ( Z Z ) 02等效于 L 图7.3.2 不均匀传输线

ANKD4.不均匀传输线的透射系数itirU++U-=U"Z=0处U++(U+-U-)/Z.=U"/ZZolZo2u-U'_Z.-Zo解得,透射系数T0ZU+-2Z.,+Zo5.沿线各点电压、电流表达式2≤0处(2)=U+(e-ip:+IeB=Ute-ipr(l+)i()=U*(e-ip--Tepp/Z,=U*er(1-F)/ZU(=)=U'e-ip: = tUre"≥>0处TU+JP2i(2)=tite-p =eZo2注意(1)坐标原点的选取;ZLL-Zo=Fej(2+1)(2)在不同情况下的表达式:(W+ZoLoLlTZ.-2(3)与的区别。1TZ,+ZoZo2+Zol
4. 不均匀传输线的透射系数 Z=0处 U +U =U + − 01 Z02 (U −U )/ Z =U/ + − 解得,透射系数 02 01 02 01 Z Z Z Z U U + − = = + 5. 沿线各点电压、电流表达式 j 2 z 2 U(z) U e U e j z − − + = = z 2 j 2 e Z U I( z ) I e 02 j z − + + − = = z 0处 U (z)=U (+ e − j1 z + L e j1 z) =U + e − j(1 z 1+ z ) z 01 j z 01 j z L j z I z U e e / Z U e 1 / Z ( )= (+ − 1 − 1 ) = + − (1 −) z 0处 注意(1)坐标原点的选取; (2) 在不同情况下的表达式; (3) L 与 z 的区别。 L ) Z Z Z Z Z Z Z Z ( 02 01 02 01 L 0 L 0 L + − = + − = , e ) Z Z Z Z ( j( 2 z ) 2 L L 0 L 0 L L + = + − =

AKKD7.3.2传输线工作状态1.行波(无反射、匹配)当Z,=Z。时,「=0,无反射,称为匹配,电压、电流为行波。U(z)-Ue-,i(-)-te-/Z匹配特点:1.电压、电流同相,振幅不变,2.能量全部被负载吸收。2.驻波(全反射)当Z,=0,,±jx时,「=e,=,全反射,称为驻波。设Z,=(开路),I,=I,则U(=)=U+(e-准+e准)=2U+cosβi=)=U(e--e)/Z=-2jUsin特点n入n元7元(n=0,1,2,)a)当电压波腹,电流波节B==-WB2n+1(2n+1)入2当B=(n=0,1.2)电压波节,电流波腹24b)时间相位差90°,无能量传播,电能与磁能在空间相互转换
7.3.2 传输线工作状态 1.行波(无反射、匹配) 当 ZL = Z0 时, L = 0 ,无反射,称为匹配,电压、电流为行波。 0 j z j z U(z) U e , I(z) U e / Z + − + − = = 匹配特点:1.电压、电流同相,振幅不变,2.能量全部被负载吸收。 2. 驻波(全反射) 当 ZL = 0 , , jx 时, e , l 1, 全反射,称为驻波。 j L l = = 设 ZL = (开路), L = 1 ,则 U( z ) U ( e e ) 2U cos z j z j z + − + = + = I(z) U ( e e )/ Z 2 jU sin z 0 j z j z + − + = − = − 特点 a)当 , 电压波腹,电流波节 当 , 电压波节,电流波腹 z = −n ( n 0,1,2, ) 2 n n z = − = − = 入 2 2n 1 z + = ( n 0,1,2 ) 4 ( 2n 1) z = + = − 入 b)时间相位差90º,无能量传播,电能与磁能在 4 空间相互转换。 入
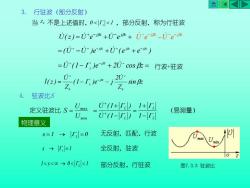
ANKD3.行驻波(部分反射)当z不是上述值时,0<<1,部分反射,称为行驻波U(z)=ute-t+u-et+Ue-i-e=(u+-u-)e-推+u-(e+e-)=U(1-)e-+2U-cosz=行波+驻波20-U+(l-r,Je-i准-ji()=sinβzZ.Z.4.驻波比S0+(1+5_1+2Umas定义驻波比S(易测量).Umin+(1--1-物理意义无反射,匹配、行波=0S=1→HaX全反射,驻波s→=]OZ1<s<80 →0<<1部分反射、行驻波图7.3.3驻波比
3. 行驻波(部分反射) 当 ZL 不是上述值时, 0 L 1 ,部分反射,称为行驻波 (U U )e U ( e e ) + − − jz − jz − jz = − + + = − + = + − − U (1 )e 2U cos z j z L 行波+驻波 sin z Z 2U (1 )e j Z U I( z ) 0 j z L 0 − − + = − − 4. 驻波比S 定义驻波比 min max U U S = 物理意义 无反射,匹配、行波 全反射,驻波 部分反射、行驻波 s = 1 → L = 0 s 1 → L = 1 s 0 1 → L (易测量) L L L L 1 1 U (1 ) U (1 ) − + = − + = + + 图7.3.3 驻波比 = + + + − j z − j z U( z) U e U e j z j z U e U e − − − − −
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第1章 自由空间中的麦克斯韦积分定律.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)目录.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第5章 根据边值观点的电准静态场.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第2章 自由空间中的麦克斯韦微分定律.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第6章 极化.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第3章 准静电学与准静磁学导言.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第4章 电准静态场 重叠积分观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第7章 传导与电准静态的电荷弛豫.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第9章 磁化.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第8章 磁准静态场 重叠积分和边值观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第10章 磁准静态弛豫和扩散.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第11章 能量 功率流和力.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第14章 一维波动力学.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第12章 电动力学场 重叠积分观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第13章 电动力学场 边值观点.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)第15章 电磁场综述.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)附录1 矢量运算.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)附录2 线积分与面积分以及旋度为矢量的证明.pdf
- 《电磁场与电磁能》课程教学课件(MIT,[美]H·A·豪斯J·R·梅尔彻,中译本)附表(微分算子、积分定理、矢量恒等式、基本常数).pdf
- 《电磁场与电磁波》课程教学资源(文献资料)国际单位.pdf
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第五章 准静态静电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第六章 平面电磁波的传播.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第四章 时变电磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第三章 恒定磁场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第二章 恒定电场.ppt
- 西安交通大学:《电磁场与电磁能》课程教学资源(PPT课件)第一章 静电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第六章 时变电磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)总结复习.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第七章 平面电磁波.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)复习题题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第五章 静态场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第三章 恒定电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.10 静电场能量、静电力.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.9 导体系统的电容.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.7 唯一性定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第四章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.6 分界面上的边界条件.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.8 镜像法.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.5 泊松方程和拉普拉斯方程.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.4 高斯通量定理.ppt
