《电磁场与电磁能》课程教学课件（MIT，[美]H·A·豪斯J·R·梅尔彻，中译本）第15章 电磁场综述

第15章电磁场综述15.0引言在开展电磁场的学习中，我们已经按照图1.0.1中所总结的路线进行。我们的探索是使由发克斯韦方程组总结的电学和磁学的定律成为理解与创新的基础。这些定律既普遍又简单。但是，只有在通过许多特例获得经验之后才能掌握它们。在本书中展开的实例研究，目的在于提供这种经验。本章将回顾这些例子并试图促进概念与应用的结合。在每一阶段，用简单的结构来说明场您样与它们的源有关，无论后者是外施的或是在材料中感应的。其中一些结构在15.1节中识别，在那里它们用来概述电准静态场，磁准静态场和电动力学场的比较研究。通过选择特定种类的结构，例如圆杜或球，并用它作为依照实例研究顺序中材料的示例，就能对大部分的概要(图1.0.1)作--回顾场与它们的源之间的关系是15.2节的主题。仍旧按照图1.0.1中的提纲，电场的源是不成对的电荷和极化电荷，而磁场的源是电流和（成对的）磁荷。从准静电学开始，接着是准静磁学，最后是电动力学，我们的提纲首先集中在源是受约束的，然后出存在的媒质感应的物理情况。在本书中，磁化用磁荷猫述。在15.2节中将介绍另一个常用的表述方式，其中磁化用“安培”电流描述。在EQS,MQS和电动力学场的讨论中，作为起点，我们采用了媒质的理想化模型。其中材料表现为“完纯导体”和“完绝缘体"，并且可以说它们有“无限大介电常数或磁导率"的这一极限情况，还提供「另一种方法来形成对材料的综述。这个方法在15.2节的最后采用。正如这些理想化是有用的样，只有在考虑到其完纯性的相对性，它们的实际意义才能被重视。虽然我们通过使材料理想化来引入它们的作用，然后我们更仔细地观察，看出“完纯性”是相对的概念。如果与理想化模型和关的场被认为是“零阶"的，则在 15.2节的第二部分中通过考虑“一阶”场的办法提高反映在回顾中的完备的水平在EQS和IMQS系统中“完纯导体”意味着什么，将是15.2节的一部分内容，它自然地导到15.3节中关于特性时间如何能用于理解电磁场与媒质的相互作用的回顾。现在我们能从电动力学的观点看EQS和MQS系统，15.3节的目的在下对空间尺度，时间尺度（频率）和材料性质如何确定主要过程的概述。这一节的日的，不仅是汇集材料，而且还要加深对往往是重复的过程的理解，由此建立使能既包含了基本的物理概念，又作为工程创新的基础的模型。能量的储存和损耗，与作用于宏观媒质相关的力一起，还提供了电磁系统另一方通的概述。这是15.4节的主题，它总结了为作么宏观力通常能分类为或者是EQS或者是MQS的理出。532 ·

15.1漂和材料的结构我们可以用许多结构中的任何一个来复习图1.0.1 中所概括的物理现象。与给定的物理情况相关的章节、例题与习题在表中注明，用来追踪一种给定结构的演变。增量偶极子在均勾媒质中，偶极子场是两维或兰维拉普拉斯方程或波动方程的简单解，并用来表示总结在表15.1.1中的情况的范围。正如在第4章中所介绍的，偶极子描述靠得很近的两个等量而异凸的电荷。这些电荷也许产生在一对靠得很近的导也物体上，如图3.3.1a所示。在第6章中，川电偶极子来描述极化，并且对不成对的和成对的(极化)电荷作出区别。表15.1.1增量偶极子的总结电准静态的电荷点：1.44线：刘题4.4.1,5.7节afg p-ad电造静态的极化稳定的传导电流at点：例7.3.2线：习题7.3.3磁澄静态的电流m-ai倒8.3线：例8.1.磁谨态的磁化di'rm-g.d9.1节电的电动力学的皖A·C点：12.2节均电动力学的Smn-a点：12.2节第7章中描述传导现象时，偶极了表示对靠得很近的电流源。偶极子是电荷守恒定律中的源，而不是高斯定律中的源。在准静磁学中，有两类偶极子。第一类是小的电流环,其中偶极矩是面积。和环行电流i的乘积。偶极子场是电流环产生的场,它远离例如图 3.3. 1 b 中所示的那和回路。如我们将在 15. 2节中讨论的，我们能够用电流环偶极子表示磁化。然而，在第9章中，磁化用一对等鼠而异号的磁一磁偶极了表示。因此，第6章中有关极化的论述可直接适用于磁化。要建之偶俊子的附变的正，负电荷，需要有电流。在图3.3.1a中，此电流由电压源供给。533

在EQS极限情况下，与此电流相关的磁场的作用可以忽略，有关的磁场也就可忽略。在第12意中，法拉第定律和安培定律是自相一致的，并发现这两个定律间的联系导致电磁辐射。电偶极子辐射的存在是因为充电电流产生磁场，而磁场又感应有旋的电场。在表15.1.1中最后所示的磁偶极子的情况中，由时变磁场感应的位移电流产生的电磁波，它本身又产生旋度更大的磁场。平面的周期性结构为了研究表15.1.2中概括的准静态及“稳定”的情况，笛卡儿坐标系中拉普拉斯方程的解全都是需要的。用于研究这些在“延伸到无限远”的平而内是周期性的物理情况的场，天然地在垂直于该平面的方向衰减。表15.1.2平面的姆期性结构场的解拉誉拉斯方程：5.4节12.5节波动方程：电准静态的（EQS）受约东的电位与电积例5. 6. N.6.1受约束的电位与作电荷：m3,6.1-4受约束的电位与极可烟6.3.1-4电荷驰豫：习遇7.9.7-8稳定传导（MQS或FQS受约束的电位与绝绿的边界：187.4.础演静态的(MQS)例9.3.2菜花通过障导体的隧扩散：习题10.41-2电动力学的外施的表面源：例12.6.1-2可题12.6.1-4有完纯导电边界的外施的源18/212.7.3-4可题13.2.1完绝绝缘的边界：13.5节可期13.2, 3-4可题13.5.1-4当频率变低时，12.6节中所研究的电动力学场有和这一样的需直于周期性的方向的衰减。根据电磁波的观点，这些低频场，基本上是可用非均匀的平面波表示的拉普拉斯场。当频率升高时，非均匀平面波变成沿它们以前衰减的方问传播的波。波动方程的解可以是在两个方向空间周期性的。表15.1.2结尾部分的TE和TM电动力学场的结构有助于使不涉及损耗的EQS和MQS结构的这些方面正确联系。圆柱形的和球形的,534

拉普拉斯方程少数简单的解答能充分说明在圆柱形的和球形的物体内和它的周围场的性质。表15.1,3表明一系列实例研究如何分别地从“完纯”绝缘体和"完纯"导体系统中的EQS和MQS场开始,而以有限电导率对 EQS 和MQS 场的非常不同的影响终结。表 15.1. 3圆柱形的和球形的结构拉骨拉斯方程场的解避柱形的；5.7节球形的：5.9节电谁静态的例15. 8,1例5.9.2永久的：可题6.3.6例6.3.1感成的：例6,6. 2例7.9.3电荷驰豫：习题7.9.4-5习题7.9.8稳定传导（MQS或EQS）外施的电流：例7.5.1习题7.5.1-2磁准静态的习题8. 5 1-2三R的可题8.4.2-3In.习脑9, 6. 3-4,10,12习题9,6.11,13习题10.4.3-4例10.4. 1习题10.4.5-6平行平面板之间的场均勾和分块均勾的准静态场充分说明从EQS的“电容器”开始到MQS的“通过薄导体的磁扩散”为止的现象，参阅表15.1.4所列。密切有关的TEM场描述剩下的情况。轴对称的(同轴的)场在表15.1.4中这一类型下总结的实例研究与平行平面导体间的场相类似。表15.1.4特殊的结构平行平面板之间的场电容器：例3. 3.1,6.3.3习题6.5.1-4,6.6.8,3.3.11.6电阻器：例[7.2.1,7.5,2例8.4.4,习题9. 5.1,3,6电感器：电荷驰豫：97.9感护通过：萍导体HW10.3厚导体（TEM):例10.6.1,10.7.可题10,3.4,10.6:1-2,10.7.1-2原潮（TEM）渡导镇式：例13.1.1-2例14. 1.1,14. 8.2传输线 535

续表轴对称的(同轴的)场电统：习题6.5.5例[7. 5.习题7.2.1,4,8@电感器:例3.4. 1习题9.5.2,1-5电荷地豫：习题7.9.1TEM传输线：1313.1.4有纵向边界条件的TM和TE易E电腾充械器TE波导场圆柱形的导体对和导体平EQS完绝导体：2S完纯导体；TEM传输线：有纵向边界条件的TM和TE场表15.1.4中在此标题下的实例研究提供了在准静态极限情况下和作为电磁波情况下了解场和它们的源之间关系的机会。通过演示5.5.1和8.6.2说明的EQS和MQS极限情况分别变成演示13.3.1和13.3.2的短接的TM和TE波导场圆柱形的导体对和导体乎面在这些结构中的场首先是EQS，然后是MQS，最后是TEM。EQS场和MQS场与物质世界的关系用演示4.7.1和8.6.1说明。不论横截面的形状如何，在-对完纯导上的TEM波与演示13.1.1中所说明的有差不多相同的性质，而与几何形状无关。15.2宏观媒质宏观媒质的源表示法EQS电场强度的主要的源是不成对的和成对的电荷密度，分别措述宏观媒质通过传导与极化对场的影响（第6章）。虽然在第8章中起因于传导的MQS磁场的主要的源是不成对的电流密度，在第9章中，把磁化模拟成是由一对正和负的磁荷组成的永久磁偶极子取向排列的结果。这不是介绍磁化的传统方式。然而，磁荷模型使极化与磁化间有相似性，使我们能够用与极化类比的办法将磁化引人场的方程。较为传统的方法是将磁化看成是环行的安培电流的果。这两个方法导致相同的最后结果，仪仅模型不同。为了说明这点，让我们根据B，而不是H重写左克斯韦方程组式(12.0.1)一(12.0.4)。VxE=-B(1)-VXM- J.+ReE+&P(2) VX-·536

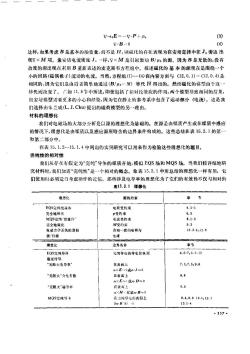
(3)VeE=-V·P+pV-B.=0(4)这样，如果考虑B是基本的场变量，而不是H，则磁化的存在表现为在安培定律中在J。旁边出现V×M项。像安培电流密度J。一样，V×M是引起激励B/μo的源。因为B是无散的，没有故度的源出现在利用B重新表述的麦克斯韦方程组中。述磁化的基本的源现在是围绕一个小的回路（磁偶极子)流动的电流。当然，方程组(1)-(4)在内容方面与(12.0.1)—(12.0.4)是相同的，因为它们是由后者简单地通过（B/μa一M）替代H得出的。然而磁化的模型由于这-格代后改变了。已如11.8节中所述，即使包括了相对论效应的作用，两个模型导致相同的结果，但安培模型需要更多的小心和经验，因为它在静止的参考系中包含了运动部分（电流）。这是我们选择由朱兰成(L.J.Chu)提出的磁荷模型的另--理由。材料的理想化我们对电磁场的大部分分析是以源的理想化为基础的。在源是由媒质产生或在媒质中感应的情况下，理想化是由媒质以及感应源所暗含的边界条件构成的。这些总结在表15.2.1的第一和第二部分中。在表15.1.2-15.1.4中列出的实例研究可以用来作为检验这些理想化的题目。完纯性的相对性我们从存在有假定为“完纯”导体的媒质开始，模拟EQS场和MQS场。当我们较详细地研究材料时，我们知道“完纯性”是一个相对的概念。象表15.2.1中所总结的理想化一样有用，它们使用时必须适当考虑所作的近似。那些涉及电导率的理想化为了它们的有效性不仅与相对的表15. 2. 1 理想化理想化草源的约束书EQS完纯绝缘体电码受药束E完全地极化P受约束电滤受药束MQS完纯"绝缘格”M受约束完全地磁化-1.违界条件幸节理想化EQS完纯导件完绝导也的等电位表面4. 6-7,5. 1-13稳定传导在表面上7.2,7. 5,9.6“无限大电导率”nXE-0nJ~09.8“无限大"介电常数在表面上nXE~（或n·D09.6“无限大”磁导来在衰面nXH-K减nB~0在范豌舒也的表面上8.4,8.6 0.1,12.7MQS完纯导发On·B'at-013.1-4.537

材料性质有关，而且与尺寸和时间变化率也有关。这些将在下节中回顾。在表中列出的三个理想化的“无限大参数”中的每一个，在一个区域中的参数值与在另一个区域中的参数值相比要大。合适的边界条作取决于场激励的区域。理想化使得在“内部”区域把场近似成为可能，而不考虑“外部”是什么。“内部”区域表面上的一个连续性条件可被近似看成是齐次的。然后从其他的连续性条件开始求得“外部”区域的场。我们对这个“内部-外部”方法的首次介绍出现在7.5节。当适当考虑用有散度的源代替有旋度的源时，9.6节中对磁化材料的一般讨论也适用于其他情况。15.3特性时间,物理过程与近似法近似定律的自洽性在处理EQS和MQS系统时，我们集中于由麦克斯韦方程组的近似形式产生的现象。在“精确”方程组中的一些项被忽略，并且场的图形是从方程组的这些合项形式导出的。这种解决问题的方式对电磁场理论来说不是唯一的。忽略掉出现在实际问题的“较精确”的公式中的一些项常常是需要的。这样做时，需要充分认识到这样近似的后果。因此，在EQS和MQS近似中所H的能量守恒关系是完整的麦克斯韦方程组所服从的玻印亭定理的特殊极限情况。忽略位移电流或电磁感应等效于忽略电的或磁的能量储存。我们需要弄清，问题是否能由方程组的近似形式充分地确定，以及哪些边界条件需要保留、哪些应除去。EQS 和 MQS 近似法的形成,以及唯一性定理的证明,提供了在一组近似方程的结构中产生自相一致体系的例子。在由“完纯导电”和“完纯绝缘”媒质组成的系统中，决定其中是否有 EQS 或 MQS 子系统是相对地容易的被完纯绝缘体包围的完纯导体系统，如果在频率为零时它是“开路"的(电容器系统)，可能是EQS,而如果在频率为零时它是“短路"的（电感器系统），就可能是MQS。然而，我们通常面临的不是材料已标明为“完纯导体"或“完纯绝缘体”的物理情况。确实，以第7章后半章和第10章作为背景，会认识到在EQS和MQS系统中，术语“完纯的”通常有很不同的意义。美折王提供·连接到电源的实际物体，我们怎样从不相连贯的电磁现象中来挑栋出主要的！通常，这是一个选代过程，而第一次“猜测”是以经验和直觉为基础的。如果实际关心的材料和几何形状的组合种类太多，以致不能作出几条普遍适用的简单规则，本节的目的不过是将我们已学过的内容加以组织，使得能增进对确定主要的物理过程所需要的理解3从有限电导率怎样影响第7章EQS系统中电荷密度的分布和第10章MQS系统中电流密度的分布的检验，以及从有损媒质电动力学的讨论，我们对确定简单子系统的电磁性质必须提什么间题有了好主意。已在14.8节中熟悉的一个特例，就是示于图14.8.1夹在完纯导电平行平面电极之间的导电块。首先，材料的电性质是什么？在这理这个问题简化为，和u是什么这些参数中范围最广的是电导率α，它能够从普通碳氢化合物液体的10-*S/in变化到调的几乎10"S/m。实际上真空和超导材料将这个范围扩展为从绝对零值到无限大·538

其次，大小尺度1是什么?在一般的工程系统中，所关心的长度范从半导体结的亚微米级到电力传输系统的超过 1000km。当然，即使这个范围,与自然界提供的从亚核的到超银河系的范围相比也是小的。第三，所关心的时间尺度是什么？也许系统是由正弦变化的源激励。那么时间尺度多半会是角频率的倒数1/@。在一般的工程实际中，频率范围从用来表征隔音的10-3Hz到光频的10"Hz范围内。仍然是自然界提供的频率范围更宽广，包括一个极端是地磁场的儿百万年的例数而另一个极端是伽马射线的频率。相似性与表克斯韦方程组考虑一示于图15.3,1的任意系统，它具有典型长度1以及特性图15.3.1具有典型长度1，介电μ的任意系统(1)ee(r),ag(r), μ(r)式中 e、α和 μ是介电常数、电导率和磁导率的典型量值,而(r),α(r)和μ(r)是空间分布,进行了归一化，使得它们的峰值大约为一从我们在 EQS 和MQS系统中对欧姆导体的研究知道，场的分布分别由电荷驰豫时间t。和磁扩散时间tm控制。此外，从我们对电磁波的研究知道，电磁波的通过时间tem与电动力学的效应一起起作用。举例说明这三个时间的章节在表15.3.1中列出。因此，我们预期会发现在具有个典型尺寸尺度的系统中，决定场的性质的时间不会多于三个。(2)Tm=μo;tom=-WueTo=i表15.3.1幸例说明特性时间的章节7.7,7.9节电准静态的电将弛像时间：110.2-7节磁准静态的碱(植流）扩散时剂：12.2-7,18.1-2 14 -4 节电磁波通过时间：实际上,电磁波通过时间是另外两个时间的儿何平均值，(3)Tem=Vtotm所以这些时间中只有两个是独立的。当激励的角频率为@时,在系统内源和场的相对分布由の 和这三个时间中的任意一对的乘积决定。这可以由将麦克斯韦方程组写成归一化形式看出。为此，我们用下面加一横杠表示归· 539-

一化的（无盘纲的)变量，并且将空间坐标对典型长度1归。时间则对角频率的数归--化。(4)(r,9,z)=(zl,9l,al),t=t/o场和电荷密度对典型电场强度e归一化。E-E,H-(5) VEH,pp于是，麦克斯韦方程组(12.0.7)一(12.0.10)与(1)式的构成定律一起成为(6)V-EE=p.E)IxH=0t.m.(7a)(7b)ot.-orm E+or.mst×E--or(8)Y.uH-0,(9)在写安培定律的另一种形式时,已科用了(3)式。在有(1)式的构成定律的系统中，两个参数确定由克斯1方程组（6)一(9)式预测的场。这些参数是由(2)式所示的特性时间与所关心的典型时间的三个比值中的任一对。对于正弦稳态，所关心的时间是1/o。这样，利用由式(7a)给出的安培定律形式附，无晟纲参数1orem，r）规定场。利用式(7b)时，参数是(otem,otm)。特性时间与特性长度显然，由频率α(或其他一些表征动态过程的时间的倒数)乘以式(2)中的特性时间构成的一个无量纲参数是把物理过程分类的关键。(10)or-we;oTm=augl';arom=wlue给定这些参数中的两个，从而就知道第三个，我们就有了对于那些物理过程是主要的一些线索。然而，即使在用一个介电常数，一个电导率和一个磁导率表征的子系统中，要确定几何形状还可能需婆共他参数。每一个尺寸间的比值就是另一个无量纲参数！首先，假定我们处理的系统中所有尺寸都有典型长度1的数量级。特性时间将使得一个准静态系统为什么或者是EQS或者是MQS成为很明显。它们也决定了当频率增加时有限电导率怎样通过电荷弛豫或者磁扩散开始起作用。出干电磁的通过时间是电荷驰豫时间和磁扩散时间的几何平均值式(3)，ten一定位于另外两个时间之间。因此，这三个时间是按两种次序之一排列的。一种是T㎡<T。，在这种情况下，时间例数的次序如图 15.3. 2a所示,，另一-种与之相反也是正确的;它的次序如图 15.3.2b。此外，如果T.离Tem很远，则我们确信ta与Tem也有很大的益别当频率增加的，我们首先碰到或者是表征EQS子系统的电荷弛像现象（图15.3.2a)，或者是MQS子系统的磁扩数现象(图15,3,2b)。EQS和1MQS系统各自的准静态定律适用的频率540

MaS-EQS-鼎吉老tm图 15. 3. 2 在频率轴,上特性时间倒数的排列次序,范围高于第一个时间倒数，但低于电磁的通过时间的倒数。在两种情况下，频率都比电磁的推迟时间的倒数低得多EQS定律从式(6)一(9)得出,其中式(7)用的是第一种形式。当法拉第定律式(8)右边的项忽略时,一种物理情况可由 EQS 定律表征。 从安培定律我们了解,当 αT。>1 时，的数量级为QTemE,而当 ar。<1时大约为(Tem/t.)E。在前一种情况,位移电流密度超过传导电流密度，我们在法抗第定律的右边发现：（oT。m）"E。在后一—种情况，传导电流密度大于位移电流密度，式(8)的右边是(oTm/t)E。因此当(otem)<1或otem/t。≤1无论哪一个是对α的更为严格的限制，法拉第定律中旋度的源就可以忽略。EQS定律占优势。较简单的类似的，论证可得出MQS定律。因为现在没有与不成对的电荷相类似的源，论证更简单。 在特性时间的排列次序像图15,3.2b 那样的情况下,MQS定律要求的赖率在磁扩数时间倒数之上，但还没有达到电磁的通过讨间的倒数。这可以从归一化的麦克斯韦方程组看出,这次采用式(7b)。因为oTen《1,式(7b)中的最后-项(位移电流)。可以忽略。于是，我们得出主要的MQS定律，即忽略了位移电流的安培定律以及磁通密度连续性定律式(9)。这次，从安培定律［忽略最后一项的式(7b))得出H～(arm/corem)E，所以法拉第定律式(8）的右边的数量级为OTm。从而,MQS定律是式(10.0. 1)—(10.0.3)。当频率增高，效使我们沿若图15.3.2的频率轴从左向右移动，我们预测与电荷弛豫、电磁波和磁扩散相关的动态现象，随着频率进入各自的特性时间倒数的范围开始起作用。实际上,因为动态过程可以建立它们自己的长度尺度(例如，集肤深度)，有时情况不是那样简单。然而，通过对这些临界频率的长度尺度1次序的观察可以获得理解。为了在一个平面内描绘电磁现象，其中一个轴反央频率的作用，而另一个轴表示长度尺度，我们将频率对一个与长度无关的特性时间。归一化。这样,对于电荷弛像的、磁扩散的和电磁波的效应是重要的频率条件，分别为0(11)mte=1(12)ot.-1-→ot.=(1/1*) --or.- (1/l*) -(13)Wtom=1-6式中特性长度是1*=-Velμ(14)在坐标基本上是长度尺度和频率的平面内，沿着频率分别等于各自特性时间倒数的一些直线示于图15.3.3。垂直轴表示归一化为特性长度的长度尺度的对数，而水平轴是频率与电荷弛豫时间乘积的对数。因此，原点是长度等于 1*和频率等于1/T。的点。·541