《电磁场与电磁波》课程教学资源（作业习题）复习题解

例1:求函数=/x2+y?+z2在点 M(1,0,1)处沿7=a,+2a,+2a方向的方向导数解：au1Oux2axax+μ?+z2auyu=0M(1,0,1)ayVay1ouau1-2OzOz

例1： 求函数 u = x 2 + y 2 + z 2 在点 M(1,0,1) 处沿 l a 2a 2a 方向的方向导数. x y z     = + + 解： 2 2 2 x y z x x u + + =    2 2 2 x y z y y u + + =   2 2 2 x y z z z u + + =   M(1,0,1) 2 1 =   x u = 0   y u 2 1 =   z u 2 2 2 x y z y y u + + =   2 1 =   x u = 0   y u 2 2 2 x y z y y u + + =   2 1 =   x u 2 1 =   z u = 0   y u 2 2 2 x y z y y u + + =   2 1 =   x u

=a+27-2a而的方向余弦为Al =a.Ax+a,Ay+a.Az11COSX32VP+2+2cosB3V12+ 22+ 2222cOS:3/12 + 22 + 22函数u在M点沿7方向的方向导数为：211121Ou+0xV223323alA

而 l 的方向余弦为  3 1 1 2 2 1 cos 2 2 2 = + +  = 3 2 1 2 2 2 cos 2 2 2 = + +  = 3 2 1 2 2 2 cos 2 2 2 = + +  = 2 1 3 2 2 1 3 2 0 3 1 2 1 =  +  +  =   l M u 点沿 l 方向的方向导数为：  函数 u 在 M ax ay az l     = + 2 + 2 l a x a y a z  = x  + y  + z      3 1 1 2 2 1 cos 2 2 2 = + +  = 3 2 1 2 2 2 cos 2 2 2 = + +  =

例2-6:真空中有电荷以体密度p均匀分布于一半径为R的球中,如图.求球内、球外的电场强度及电位解：R口求电场强度：C(R,0,P)取球心为球生标系的原点。应用高斯通量定理求解较为方便。fE.ds-Zg球内ｒ<RS面取半径为r的球面。60S因电荷分布为球对称，故E的方向为 aR 方向，且仅为r的函数。 fe ds=arE(r)-ax4m2-Zg)1 4rrp6360S

例2-6:真空中有电荷以体密度 均匀分布于一半径 为R的球中,如图.求球内．球外的电场强度及电位.  解： o R  ❑ 求电场强度： 应用高斯通量定理求解较为方便。 0     = q E dS S    S面取半径为 r 的球面。 因电荷分布为球对称，故 的方向为 方向，且 仅为 r 的函数。 aR  E  取球心为球坐标系的原点。 (R,,)      3 0 0 2 1 1 3 1 4 ( ) 4 r q E dS a E r a r R R S   =  =  =       球内 r < R

3QQprE,(r)p4元R34360元R33pr即E;(r)= R 360fE.ds-Eq球外ｒ>RS面取半径为 r的球面6SZq1 4fE,·ds =anE,(r).ax4mr?元Rp38%%0sPR3E,(r)=ar故 3c0l

0 3 r E (r)    1 = 即 0 R 3 r E (r) a     1 = 0     = q E dS S         3 0 0 2 2 2 3 1 4 ( ) 4 R q E dS a E r a r R R S   =  =  =       2 3 2 3 r R E (r) a 0 R     故 = 球外 r > R 3 3 4 3 3 4 R Q R Q    = = S面取半径为 r 的球面

口求电位：选无穷远处为电位参考点球外r>Rp() =r E, di-eR?360r2:dr球内 R()=" +·dirardi +JPR'.. Φ(r) =JR360r2aR-dl380°PR3dr+drR38360(3R-r)680

❑ 求电位： 选无穷远处为电位参考点 球外 r > R   =  r (r) E dl    2 球内 r < R    =  +  R R r (r) E dl E dl       1 2     =  +  R R R r R a dl r R a dl r (r)     2 0 3 3 0 3        =  +  R R r dr r R dr r 2 0 3 3 0 3    (3 ) 6 2 0 = R − r     =  r dr r R 2 0 3 3 

例：如图所示，一无限长同轴电缆芯线通有均匀分布的电流I外导体通有均匀的等量反向电流，求各区域的磁感应强度。取柱坐标系，由于电流分布是均匀的且轴对解：称，故它所产生的磁场也应该是轴对称的，即B的大小只与半径r有关，与无关。1．r<R,区域，在该区域内均匀分布着电流密度为=/2的电流，如取半径为的圆为积分回路，据安培环路定律olfB.di = Je" Bugrdp = HoJ,mr2 2mrBi, =RB, =MolrBre = Lolra即2元R?2元R

例：如图所示，一无限长同轴电缆芯线通有均匀分布的电流I， 外导体通有均匀的等量反向电流，求各区域的磁感应强度。 解： 取柱坐标系，由于电流分布是均匀的且轴对 称， 故它所产生的磁场也应该是轴对称的， 即 B 的大小只与半径 有关，与 无关。  r  1. 区域，在该区域内均 匀分布着电流密度为 的 电流，如取半径为 的圆为积 分回路，据安培环路定律 R1 r 2 1 1 R I J  = r < 2 0 1 2 0 1 B dl B rd J r C      =  =     即 2 2 1 0 2 1 r R I rB    = 2 1 0 1 2 R Ir B    =    a R Ir B   2 1 0 1 2 =

2.．R<r<R,区域，同理取一半径为 r 的圆为积分回路，则有f B, di -f. B,a, a,rdp= (rdo=uMoluolBB202元2元r3．R,<r< R,区域，在该区域中均匀分布着电流密度为/元(R2-R2）的反向电流。同理取一半径为r的圆为积分回路，则有" B3rdp= μ[I - J,(r2 - R,)]

2. 区域，同理取一半径为 的圆为积分 回路，则有 R1 < < r R2 r B dl B a a rd B rd I C C 0 2 0 2 2  2     =    =  =           a r I B2   2 0 = 3. 区域，在该区域中均匀分布着电流密 度为 的反向电流。同理取一半 径为 r 的圆为积分回路，则有 2 R3 R < < r ( ) 2 2 2 3 2 R R I J − =  [ ( )] 2 2 2 0 2 2 0 B3 rd = I − J r − R       r I B2    2 0 =

R,2LoB3。 =2元rR?-Rr2RB, = LolaR?-R?2元r4．r >R,区域，在半径为』r的积分回路中电流的代数和为零，则B=0ul故B=LolrB.2元R2元-r2R?B, = oL. aB0C2元rR2-R2

   a R R R r r I B   2 2 2 3 2 2 0 3 3 2 − − =  B4 = 0  4. 区域，在半径为 的积分回路 中电流的代数和为零，则 r R3 r >    a R Ir B   2 1 0 1 2 =    a r I B2   2 0 =    a R R R r r I B   2 2 2 3 2 2 0 3 3 2 − − =  B4 = 0  故 2 2 2 3 2 2 0 3 3 2 R R R r r I B − − =    

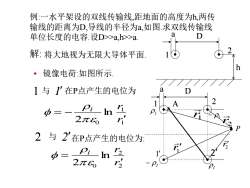
例：一水平架设的双线传输线,距地面的高度为h,两传输线的距离为D导线的半径为a.如图.求双线传输线aD单位长度的电容.设D>>a,h>>a.解：将大地视为无限大导体平面16h·镜像电荷·如图所示2D1与1'在P点产生的电位为APiriInPid=2元%r'2与2'在P点产生的电位为：r2PiInd2元%r2BD

例:一水平架设的双线传输线,距地面的高度为h,两传 输线的距离为D,导线的半径为a,如图.求双线传输线 单位长度的电容.设D>>a,h>>a. a h D 1 解 2 : 将大地视为无限大导体平面. • 镜像电荷:如图所示. 1 与 1 在P点产生的电位为 1 1 0 ln 2 r r l  = −     r2  a D 1 2 1 2  l  l − l − l P r1  1 r   2 r   A 2 与 2 在P点产生的电位为: 2 2 0 ln 2 r r l  =    

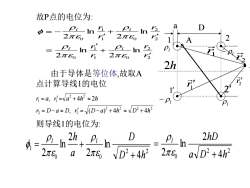
故P点的电位为：aDr2PPln1n2元%2元6%r2rAriPrPir2PiInInr'2元%2元%r2h由于导体是等位体.故取AT点计算导线1的电位1r=a, r=va +4h ~2hDr=D-a=D,r=(D-a)+4h?~D+4h2则导线1的电位为D2hD2hPiPiPiIrα2元2元%2元avD2+4h2VD?+4h?

故P点的电位为: 2 2 1 0 1 0 2 2 1 0 1 0 ln 2 ln 2 ln 2 ln 2 r r r r r r r r l l l l  +  =  +  = −              r2  a D 1 2 1 2  l  l − l − l P r1  1 r   2 r   A 由于导体是等位体,故取A 点计算导线1的电位 2 2 2 2 2 2 2 1 1 , ( ) 4 4 , 4 2 r D a D r D a h D h r a r a h h = −  2  = − +  + =  = +  则导线1的电位为: 2 2 0 0 1 4 ln 2 2 ln 2 D h D a h l l + = +        2 2 0 4 2 ln 2 a D h l hD + =    2h