《电磁场与电磁波》课程授课教案（讲义）静态场的边值问题

课程：电磁场与电磁波内容：第5章静态场的边值问题课时：6学时石河子大学信息科学与技术学院

1 课程: 电磁场与电磁波 内容: 第 5 章 静态场的边值问题 课时:6 学时 石河子大学信息科学与技术学院

课题科目静态场的解电磁场与电磁波课时教师6 学时时间授课班级~学年第 学期知识目标：1、认识静态场。教学目的2、理解静态场中的麦克斯韦方程组与要求3、理解泊松方程的定义和概念。4、理解拉普拉斯方程的定义和概念。5、理解对偶原理在电磁场求解中的应用。6、理解三类边界条件的定义和概念。7、理解叠加原理在电磁场求解中的应用8、理解唯一性定理在电磁场求解中的应用9、理解镜象法的概念及其应用。10、理解分离变量法的概念及其应用。11、理解格林函数法的概念及其应用。12、理解有限差分法的概念及其应用。能力目标：根据学生已具备的关于方面数学知识和物理知识，引导学生从基本原理出发了解电磁场的求解方法，培养学生的想象力及利用所学知识分析、总结问题的能力。情感目标：引导学生将抽象的数学分析与现实物理世界尽可能融

2 课 题 静态场的解 科目 电磁场与电磁波 课 时 6 学时 教师 授课班级 时间 ～ 学年第 学期 教学目的 与要求 知识目标： １、认识静态场。 ２、理解静态场中的麦克斯韦方程组。 ３、理解泊松方程的定义和概念。 ４、理解拉普拉斯方程的定义和概念。 5、理解对偶原理在电磁场求解中的应用。 6、理解三类边界条件的定义和概念。 7、理解叠加原理在电磁场求解中的应用。 8、理解唯一性定理在电磁场求解中的应用。 9、理解镜象法的概念及其应用。 10、理解分离变量法的概念及其应用。 11、理解格林函数法的概念及其应用。 12、理解有限差分法的概念及其应用。 能力目标： 根据学生已具备的关于方面数学知识和物理知识，引导 学生从基本原理出发了解电磁场的求解方法，培养学生的想 象力及利用所学知识分析、总结问题的能力。 情感目标： 引导学生将抽象的数学分析与现实物理世界尽可能融

合，激发学生对理论学习的热情。静态场是指场量不随时间变化的场。静态场包括：静电场、恒定电场及恒定磁场，它们是时变电磁场的特例。分析静态场，必须从麦克斯韦方程组这个电磁场的普遍规律出发，导出静态场中的麦克斯韦方程组，即描述静态场特性的基本方程。再根据它们的特性，联合物概述态方程推导出位函数的泊松方程和拉普拉斯方程。最后，静态场问题可归结为求泊松方程和拉普拉斯方程解的问题。通常求解这两个方程的方法有：镜像法、分离变量法和复变函数法，它们属于解析法，而在近似计算中常用有限差分法泊松方程和拉普拉斯方程、对偶原理、叠加原理和唯一性定理、镜像教学重点法、分离变量法。教学难点镜像法、分离变量法。教学方法讲述法、演示法、发现法、讨论法教学环境多媒体教室教学准备多媒体课件1、复习提问2、引入新课3、讲解新课教学过程4、归纳总结5、布置作业学时分配泊松方程与拉普拉斯方程，对偶原理、叠加与唯一性定2学时

3 合，激发学生对理论学习的热情。 概述 静态场是指场量不随时间变化的场。静态场包括：静电场、恒定 电场及恒定磁场，它们是时变电磁场的特例。分析静态场，必须从麦 克斯韦方程组这个电磁场的普遍规律出发，导出静态场中的麦克斯韦 方程组，即描述静态场特性的基本方程。再根据它们的特性，联合物 态方程推导出位函数的泊松方程和拉普拉斯方程。最后，静态场问题 可归结为求泊松方程和拉普拉斯方程解的问题。通常求解这两个方程 的方法有：镜像法、分离变量法和复变函数法，它们属于解析法，而 在近似计算中常用有限差分法。 教学重点 泊松方程和拉普拉斯方程、对偶原理、叠加原理和唯一性定理、镜像 法、分离变量法。 教学难点 镜像法、分离变量法。 教学方法 讲述法、演示法、发现法、讨论法 教学环境 多媒体教室 教学准备 多媒体课件 教学过程 1、复习提问 2、引入新课 3、讲解新课 4、归纳总结 5、布置作业 学时分配 泊松方程与拉普拉斯方程，对偶原理、叠加与唯一性定 2 学时

理镜像法、2 学时2 学时分离变量法、格林函数法小计6 学时教学环节教学过程

4 理 镜像法、 2 学时 分离变量法、格林函数法 2 学时 小计 6 学时 教学环节 教学过程

多媒体课件展示：第5章静态场的解边值问题引入提示：本章的重点内容新课设置悬念、激发探究提问：你对求解电磁场有什么了解讲述多媒体课件展示：5.1泊松方程和拉普拉斯方程新课1、静态场的麦克斯韦方程组所具有的形式。2、静电场的基本方程。VxE=0V.D=p上式说明，静电场中E的旋度为0，静电场是一个有源无旋场，即静电场中的电场不可能由旋涡源产生；电荷p是产生电场的通量源。电介质的物态方程为D=E静电场是一个位场，可用电位函数来描述，即E--Vo3、恒定电场的基本方程。VxE=0V.J=0上式表明，除电源以外的区域中电场强度的旋度为零，说明这些区域可以看成是一个位场，恒定电场的电流线是闭合曲线。导体中的物态方程为J=αE从以上分析可知，恒定电场的无源区域也是一个位场，也可用一个标量函数来描述。4、恒定磁场的基本方程

5 引入 新课 讲述 新课 多媒体课件展示：第 5 章 静态场的解边值问题 提示：本章的重点内容 设置悬念、激发探究 提问：你对求解电磁场有什么了解？ 多媒体课件展示：5.1 泊松方程和拉普拉斯方程 1、静态场的麦克斯韦方程组所具有的形式。 2、静电场的基本方程。   E = 0   D =  上式说明，静电场中 E 的旋度为 0，静电场是一个有源无旋场，即静电 场中的电场不可能由旋涡源产生；电荷  是产生电场的通量源。电介质 的物态方程为 D =  E 静电场是一个位场，可用电位函数  来描述，即 E = − 3、恒定电场的基本方程。   E = 0   J = 0 上式表明，除电源以外的区域中电场强度的旋度为零，说明这些区域可 以看成是一个位场，恒定电场的电流线是闭合曲线。 导体中的物态方程为 J E = 从以上分析可知，恒定电场的无源区域也是一个位场，也可用一个标量 函数来描述。 4、恒定磁场的基本方程

VxH-JV.B=0上式说明电流是产生恒定磁场的旋涡源，磁场不可能由通量源产生，根在这种情况下我们可以引入一个矢量磁位函数。B=μH磁介质中的物态方程：由以上分析可知，恒定磁场是一个旋涡场，电流是这个旋涡场的源，电流线是闭合的。5、泊松方程和拉普拉斯方程：静电场既然是一个位场，就可以用一个标量函数的梯度来表示它，即E=-V对于均匀、线性、各向同性的介质，为常数，V=0，所以V.D=V.(SE)=V.E=peV-(-V0)=p即V20=-上式即为在有电荷分布的区域内，或者说在有“源”的区域内，静电场的电位函数所满足的方程，我们将这种形式的方程称为泊松方程。如果场中某处有β=0，即在无源区域，则上式变为V20=0我们将这种形式的方程称为拉普拉斯方程。它是在不存在电荷的区域内，电位函数应满足的方程在无源区域，恒定电场的位函数满足拉普拉斯方程；磁位函数也满足拉普拉斯方程。结论：静态场可以用位函数表示，而且位函数在有源区域均满足泊松方程，在无源区域均满足拉普拉斯方程。多媒体课件展示：5.2对偶原理6

6   H = J   B = 0 上式说明电流是产生恒定磁场的旋涡源，磁场不可能由通量源产生，根 在这种情况下我们可以引入一个矢量磁位函数。 磁介质中的物态方程： B = H 由以上分析可知，恒定磁场是一个旋涡场，电流是这个旋涡场的源，电 流线是闭合的。 5、泊松方程和拉普拉斯方程：静电场既然是一个位场，就可以用一个 标量函数  的梯度来表示它，即 E = − 对于均匀 、线 性、各 向同性 的介质 ，ε 为常数 ,  = 0 ，所以   D =  (E) =   E =   (−) =  即     = − 2 上式即为在有电荷分布的区域内，或者说在有“源”的区域内，静 电场的电位函数  所满足的方程，我们将这种形式的方程称为泊松方 程。如果场中某处有ρ=0，即在无源区域，则上式变为 0 2   = 我们将这种形式的方程称为拉普拉斯方程。它是在不存在电荷的区域 内，电位函数  应满足的方程。 在无源区域，恒定电场的位函数满足拉普拉斯方程；磁位函数也满 足拉普拉斯方程。 结论：静态场可以用位函数表示，而且位函数在有源区域均满足泊松方 程，在无源区域均满足拉普拉斯方程。 多媒体课件展示：5.2 对偶原理

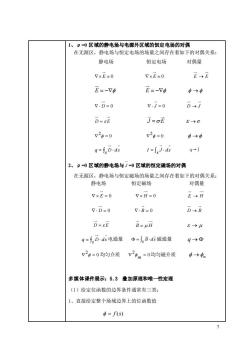
1、β=0区域的静电场与电源外区域的恒定电场的对偶在无源区，静电场与恒定电场的场量之间存在着如下的对偶关系：静电场恒定电场对偶量VxE=0E-EVXE=0E=--VdE=-Vo$→0V.D=0v.J=0D-jD=6EJ=oE8→20=0V20=0$→q=f,D.dsI=J,j.dsq-12、p=O区域的静电场与J=0区域的恒定磁场的对偶在无源区，静电场与恒定磁场的场量之间存在着如下的对偶关系：对偶量静电场恒定磁场E-HVXE=0VxH=0D-BV.D=0V.B=0D=6EB=μH6→uq=f,D.ds电通量=J,B.ds磁通量q→02=0均匀介质20m=0均匀磁介质Φ→0m多媒体课件展示：5.3叠加原理和唯一性定理（1）给定位函数的边界条件通常有三类：1、直接给定整个场域边界上的位函数值=f(s)

7 1、ρ=0 区域的静电场与电源外区域的恒定电场的对偶 在无源区，静电场与恒定电场的场量之间存在着如下的对偶关系： 静电场 恒定电场 对偶量  = E 0  = E 0 E → E E = − E = −   →   D = 0   J = 0 D → J D =  E J E =  → 0 2   = 0 2   =   → d s s q = D   d s s I = J   q→I 2、ρ=0 区域的静电场与 J =0 区域的恒定磁场的对偶 在无源区，静电场与恒定磁场的场量之间存在着如下的对偶关系： 静电场 恒定磁场 对偶量   E = 0   H = 0 E → H   D = 0   B = 0 D → B D =  E B =  H  →  d s s q = D   电通量 B d s s  =   磁通量 q → 0 2   = 均匀介质 0 2  = m  均匀磁介质   → m 多媒体课件展示：5.3 叠加原理和唯一性定理 （1）给定位函数的边界条件通常有三类： 1、直接给定整个场域边界上的位函数值  = f (s)

式中f(s)为边界点S的位函数，这类问题称为第一类边界条件。2、只给定待求位函数在边界上的法向导数值%- T(0)因为Ps=Dn=εEn=-e%。故上式相当于给定了边界表面的面电荷密度或电场强度的法向分量，这类问题称为第二类边界条件。3、给定边界上的位函数及其法向导数的线性组合：$+()%=12()这是混合边界条件，称为第三类边界条件。（2）叠加原理：若和分别满足拉普拉斯方程，即=0和Vd,=0,则和z的线性组合：=agb2必然也满足拉普拉斯方程：V2(ag,+b2）=0，式中a、b均为常系数。（3）唯一性定理：对于任一静态场，在边界条件给定后，空间各处的场也就唯一地确定了，或者说这时拉普拉斯方程的解是唯一的。多媒体课件展示：5.4 镜象法提示：镜象法是利用一个与源电荷相似的点电荷或线电荷来代替或等效实际电荷所产生的感应电荷，这个相似的电荷称为镜象电荷，然后通过计算由源电荷和镜象电荷共同产生的合成电场，而得到源电荷与实际的感应电荷所产生的合成电场，这种方法称为镜象法。举例说明镜象法的应用方法。8

8 式中 f (s) 为边界点 S 的位函数，这类问题称为第一类边界条件。 2、只给定待求位函数在边界上的法向导数值 f (s) n =   因为 s n n D E n      = = = −  。故上式相当于给定了边界表面的面电荷密 度或电场强度的法向分量，这类问题称为第二类边界条件。 3、给定边界上的位函数及其法向导数的线性组合： ( ) 2 ( ) 1 f s n f s =   +   这是混合边界条件，称为第三类边界条件。 （2）叠加原理：若 1 和 2 分别满足拉普拉斯方程，即 1 0 2   = 和 2 0 2   = ,则 1 和 2 的线性组合：  = a1 +b 2 必然也满足拉普拉斯 方程： 1 2  (a +b 2 ）=0，式中 a、b 均为常系数。 （3）唯一性定理：对于任一静态场，在边界条件给定后，空间各处的 场也就唯一地确定了，或者说这时拉普拉斯方程的解是唯一的。 多媒体课件展示：5.4 镜象法 提示：镜象法是利用一个与源电荷相似的点电荷或线电荷来代替或等效 实际电荷所产生的感应电荷，这个相似的电荷称为镜象电荷，然后通过 计算由源电荷和镜象电荷共同产生的合成电场，而得到源电荷与实际的 感应电荷所产生的合成电场，这种方法称为镜象法。 举例说明镜象法的应用方法

提示：1、镜象电荷不能放在要讨论的区域中，放在被讨论的区域中时将会改变所放置区域的电位分布，所得出的电位将不满足原来的拉普拉斯方程或泊松方程。2、镜像电荷周围的介质应该是与被讨论的区间一致的3、所得电位函数必须满足原来的边界条件4、可以用类似的方法来处理两种磁介质分界面两边的磁场计算问题。多媒体课件展示：5.5分离变量法分离变量法是求解拉普拉斯方程的基本方法，该方法把一个多变量的函数表示成为几个单变量函数的乘积后，再进行计算。与完全的数学求解不同，针对具体物理问题使用该方法求解时，将要结合一些物理概念进行分析求解。通过分离变量，它将函数的偏微分方程分解为带“分离”常数的几个单变量的常微分方程。不同坐标系分解出来的单变量常微分方程的形式不同，其通解的形式也不同。坐标系的选择应尽量使场域边界面平行于坐标面。例如：矩形域应选直角坐标系；圆柱形域应选圆柱坐标系：球形域应选球坐标系。举例说明在直角坐标系和圆柱坐标系下的分离变量法，多媒体课件展示：5.6格林函数法格林函数法是数学物理方法中的基本方法之一，可以用于求解静态场中的拉普拉斯方程、泊松方程以及时变场中的亥姆霍兹方程。在线性电路理论中，为了求一线性电路对任意激励的全响应，我们一般是在求得单位冲击响应的基础上，先求出零状态响应，然后再加上零输入响应。所谓格林函数法就是上述方法在空间域中的应用。边值问题中的单位冲9

9 提示： 1、镜象电荷不能放在要讨论的区域中，放在被讨论的区域中时将会改 变所放置区域的电位分布，所得出的电位将不满足原来的拉普拉斯方程 或泊松方程。 2、镜像电荷周围的介质应该是与被讨论的区间一致的。 3、所得电位函数必须满足原来的边界条件。 4、可以用类似的方法来处理两种磁介质分界面两边的磁场计算问题。 多媒体课件展示：5.5 分离变量法 分离变量法是求解拉普拉斯方程的基本方法，该方法把一个多变量 的函数表示成为几个单变量函数的乘积后，再进行计算。与完全的数学 求解不同，针对具体物理问题使用该方法求解时，将要结合一些物理概 念进行分析求解。 通过分离变量，它将函数的偏微分方程分解为带“分离”常数的几 个单变量的常微分方程。不同坐标系分解出来的单变量常微分方程的形 式不同，其通解的形式也不同。坐标系的选择应尽量使场域边界面平行 于坐标面。例如：矩形域应选直角坐标系；圆柱形域应选圆柱坐标系； 球形域应选球坐标系。 举例说明在直角坐标系和圆柱坐标系下的分离变量法。 多媒体课件展示：5.6 格林函数法 格林函数法是数学物理方法中的基本方法之一，可以用于求解静态 场中的拉普拉斯方程、泊松方程以及时变场中的亥姆霍兹方程。在线性 电路理论中，为了求一线性电路对任意激励的全响应，我们一般是在求 得单位冲击响应的基础上，先求出零状态响应，然后再加上零输入响应。 所谓格林函数法就是上述方法在空间域中的应用。边值问题中的单位冲

击响应函数就是格林函数。更确切地说，格林函数是单位点源（8函数源）在一定的边界条件下所建立的场的位函数，因而格林函数又称为源函数。已知电荷分布就是已知空间电场激励源的分布，因此只要知道点源的场，即可用叠加原理求出任意源的场。格林函数的解题步骤是：首先用镜像法或其他方法找到与待求问题对应的格林函数，然后将它代入由格林第二恒等式导出的积分公式即得所求。一般情况下，该积分有两项；一项为零边值响应，另一项为零激励响应。简要介绍：格林函数法的应用。多媒体课件展示：5.7有限差分法有限差分法是一种近似数值计算法，在一些工程技术计算中被广泛归纳使用。这种方法是在待求场域内选取有限个离散点，在各个离散点上以差分方程近似代替各点上的微分方程，从而把以连续变量形式表示的位总结函数方程，转化为以离散点位函数值表示的方程组。结合具体边界条件，求解差分方程组，即得到所选的各个离散点上的位函数值。有限差分法不仅能处理线性问题，还能处理非线性问题；不仅能求解拉普拉斯方程也能求解泊松方程；不仅能求解任意静态场的问题，也能求解时变场的问题；而且这种方法不受边界形状的限制。简要介绍：格林函数法的应用。本章要点1、静态场是指场量不随时间变化的场。静态场包括：静电场、恒定电场及恒定磁场，它们是时变电磁场的特例。本章从麦克斯韦方程组这

10 归纳 总结 击响应函数就是格林函数。更确切地说，格林函数是单位点源（  函数 源）在一定的边界条件下所建立的场的位函数，因而格林函数又称为源 函数。已知电荷分布就是已知空间电场激励源的分布，因此只要知道点 源的场，即可用叠加原理求出任意源的场。 格林函数的解题步骤是：首先用镜像法或其他方法找到与待求问题 对应的格林函数，然后将它代入由格林第二恒等式导出的积分公式即得 所求。一般情况下，该积分有两项；一项为零边值响应，另一项为零激 励响应。 简要介绍：格林函数法的应用。 多媒体课件展示：5.7 有限差分法 有限差分法是一种近似数值计算法，在一些工程技术计算中被广泛 使用。这种方法是在待求场域内选取有限个离散点，在各个离散点上以 差分方程近似代替各点上的微分方程，从而把以连续变量形式表示的位 函数方程，转化为以离散点位函数值表示的方程组。结合具体边界条件， 求解差分方程组，即得到所选的各个离散点上的位函数值。有限差分法 不仅能处理线性问题，还能处理非线性问题；不仅能求解拉普拉斯方程， 也能求解泊松方程；不仅能求解任意静态场的问题，也能求解时变场的 问题；而且这种方法不受边界形状的限制。 简要介绍：格林函数法的应用。 本章要点 1、静态场是指场量不随时间变化的场。静态场包括：静电场、恒定电 场及恒定磁场，它们是时变电磁场的特例。本章从麦克斯韦方程组这