《电磁场与电磁能》课程PPT教学课件（马冰然版）第二章 静电场 2.9 导体系统的电容

第二章2.92.9导体系统的电容禁q电容：-qqUU两导体之间的电容：-qq定义CU单位：法拉（F）孤立导体的电容：可将其视为孤立导体与无穷远处的另一导体之间的电容。q则CdC只与导体的形状、尺寸、位置及周围的介质相关，与带电量无关。2025-6-11

2025-6-11 第二章 2.9 1 2.9 导体系统的电容 一 、电容： 两导体之间的电容： 定义 U q C  单位：法拉（F） 孤立导体的电容： 可将其视为孤立导体与无穷远处的另一导体之间的电容。 则 q C   C只与导体的形状、尺寸、位置及周围的介质 相关，与带电量无关。 q q U q  q U

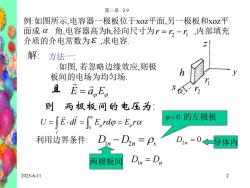
第二章2.9例:如图所示,电容器一极板位于xoz平面,另一极板和xoz平面成 α角,电容器高为h,径向尺寸为r=r,-r,内部填充介质的介电常数为℃求电容Z解：方法一如图，若忽略边缘效应,则极板间的电场为均匀场且 E=a,E,则两极板问的电压为：=0的左极板U=[E.di -[E,rdp=E,rα利用边界条件：Din-D2n=PsD2n, = 0导体内Din = Da两极板间22025-6-11

2025-6-11 第二章 2.9 2 x y z 1r 2  r 例:如图所示,电容器一极板位于xoz平面,另一极板和xoz平 面成 角,电容器高为h,径向尺寸为 ,内部填充 介质的介电常数为 ,求电容.  2 1 r  r  r  解: 如图, 若忽略边缘效应,则极 板间的电场为均匀场. 且 E E a    则 两极板间的电压为:      U E dl E rd E r l      0   利用边界条件: D1n  D2n  s   0 的左极板 0 D2n  导体内 两极板间 D1n  D 方法一: h

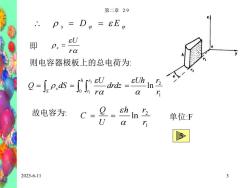
第二章2.9D= εE禁:U即福p.rα则电容器极板上的总电荷为：:Uh2072Q=1drdznαrrαch9r2故电容为：CIn单位:FUαri52025-6-11

2025-6-11 第二章 2.9 3     s  D   E 即    r U s  则电容器极板上的总电荷为: 1 2 0 ln 2 1 r Uh r drdz r U Q dS h r S r s            故电容为: 1 2 ln r h r U Q C     单位:F 5

第二章2.9方法二：心若α很小,电容器的径向尺寸比其极板的距离大许多可近似认为电容器由许多个小平行板电容器并联而成令小电容器宽度为dr，高度为h,则极板间隔和面积分别为d=rαdS = hdrchdredsdc =由定义Ddrα则总电容为chFα公2025-6-11

2025-6-11 第二章 2.9 4 方法二: 若 很小,电容器的径向尺寸比其极 板的距离大许多.可近似认为电容器由许 多个小平行板电容器并联而成,令小电 容器宽度为dr ,高度为h ,则极板间隔 和面积分别为  dS hdr d r    由定义    r hdr d dS dC   则总电容为 F r h r dr r h C dC r r 1 2 ln 2 1 1          dr r

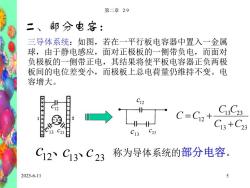
第二章2.9二、 部分电容：装三导体系统：如图，若在一平行板电容器中置入一金属球，由于静电感应，面对正极板的一侧带负电，而面对负极板的一侧带正电，其结果将使平板电容器正负两极板间的电位差变小，而极板上总电荷量仍维持不变。电容增大。C12C=C13 +C23C23C13称为导体系统的部分电容C12\Ci3\C23 2025-6-11

2025-6-11 第二章 2.9 5 二、部分电容： 三导体系统：如图，若在一平行板电容器中置入一金属 球，由于静电感应，面对正极板的一侧带负电，而面对 负极板的一侧带正电，其结果将使平板电容器正负两极 板间的电位差变小，而极板上总电荷量仍维持不变。电 容增大。 13 c 12 c 23 c 13 23 13 23 12 C C C C C C    13 c 23 c 12 c c12、c13、23 c 称为导体系统的部分电容

第二章2.9有两个以上导体的系统称为多导体系统。其中每个导体所带的电量都会影响其它导体的电位，在线性媒质中，应用叠加原理，就可得到每个导体的电位和各导体所带电量的关系。设N个导体所带电量分别为91，92，，N；N个导体的电位分别为d,Φ2.Φ3,Φ。2025-6-116

2025-6-11 第二章 2.9 6 有两个以上导体的系统称为多导体 系统。其中每个导体所带的电量都会影 响其它导体的电位，在线性媒质中，应 用叠加原理，就可得到每个导体的电位 和各导体所带电量的关系。 设N个导体所带电量分别为 2 N q ,q , ,q 1 ； N个导体的电位分别为     N , , , 1 2 3

第二章2.9则d=P1i+P1292+..·+Pinqn装2=P219i +P2292 +.:·+P29n(2-9-1)D=PN10+PN292+...+PNA即[］=［]10pipü为电位系数，只与导体的形状、尺寸、位置及周围介质有关。2025-6-11

2025-6-11 第二章 2.9 7 则     P  q  . 1  p11q1  p12q2  p1NqN N N p q p q p q 2  21 1  22 2  2 N N N NN N  p q  p q  p q  1 1 2 2 即 （2-9-1） 10 ii ij p p 为电位系数，只与导体的形状、尺寸、位置及周围介质有关

第二章2.9其中 pi为自电位函数;店电位系数的物理意义：Pi是除导体i以外，其余导体均不带电时，其自身电位与电量之比。即piqigr=q2=.=qi-1=qi+1=...=q=0当 q,=1C 时,Pi =Φ,2025-6-11a

2025-6-11 第二章 2.9 8 电位系数的物理意义： 是除导体 以外，其余导体均不带电时，其自身 电位与电量之比。 pii i 即 0 1  2    1   1     i i N i q q q q q i ii q p     ii 其中 pii为自电位函数； 当 qi 1C 时，pii  i

第二章2.9Pi是除导体i以外，其余导体均不带电时，紫其i导体的电位与i导体所带电量之比。新d即Pq11=2=.. =q j-1=q j+1=...=qn =0当 q,=1C时，pP，（i≠j）为互电位函数。互易且 Pi=Pji上2025-6-11

2025-6-11 第二章 2.9 9 0 1  2   1   1     j j N q q q q q j i ij q p    是除导体 以外，其余导体均不带电时， 其 i 导体的电位与 j 导体所带电量之比。 即 p (i j) ij  为互电位函数。 且 ij ji p  p 互易 pij j 当 qj 1C 时， 。 pij  i 7

第二章2.9求解方程组（2-9-1）得：qi = βudi + β122 +... + βinΦnq2 = β21di + β2202 +... + β2nΦn(2-9-2)qn = βn1gt+ βn202 +...+ βnndnβi电容系数β,=βri感应系数?β,(i±j)互易[g]=[β[o]=[pF[i102025-6-11

2025-6-11 第二章 2.9 10 求解方程组（2-9-1）得： ７ . N N q1   111   12 2    1  N N q2   211   22 2    2  N N N NN N q   11   2 2      ii 电容系数 (i j) ij  感应系数 ij ji 互易 （2-9-2）       １2 1 q   p