《电磁场与电磁能》课程PPT教学课件（杨儒贵版）第七章 时变电磁场

第七章时变电磁场主要内容位移电流，麦克斯韦方程，边界条件，位函数能量流动密度矢量，正弦电磁场，复能流密度矢量7-1位移电流由第四章获悉，电流分为两种：传导电流与运流电流。传导电流是导体中的自由电子（或空穴）或者是电解液中的离子运动形成的电流。运流电流是电子、离子或其它带电粒子在真空或气体中运动形成的电流

第七章 时变电磁场 主 要 内 容 位移电流，麦克斯韦方程，边界条件，位函数 能量流动密度矢量，正弦电磁场，复能流密度矢量 7-1 位移电流 由第四章获悉，电流分为两种：传导电流与运流电 流。 运流电流是电子、离子或其它带电粒子在真空 或气体中运动形成的电流。 传导电流是导体中的自由电子（或空穴）或者 是电解液中的离子运动形成的电流

可见，无论是那一种电流，都是带电粒子的运动，也就是电荷的有规则的运动。但是，位移电流不是电荷的运动，而是一种人为定义的概念。已知电荷守恒原理为apaqd. J.ds :V.atataq_ap2=0对于静态场，因，由此导出电流连atat续性原理：V.J=0J.ds =0q±0ap,0不可能根据对于时变电磁场，因atat电荷守恒原理推出电流连续性原理。但是电流连续是客观存在的物理现象，为此必须扩充前述的电流概念

可见，无论是那一种电流，都是带电粒子的运动， 也就是电荷的有规则的运动。但是，位移电流不是电 荷的运动，而是一种人为定义的概念。 已知电荷守恒原理为 d S q t   = −   J S t    = −  J d 0 S  =  J S  J = 0 对于静态场，因 ，由此导出电流连 续性原理： = 0   =   t t q  对于时变电磁场，因 ，不可能根据 电荷守恒原理推出电流连续性原理。 0 ;  0      t t q  但是电流连续是客观存在的物理现象，为此必须 扩充前述的电流概念

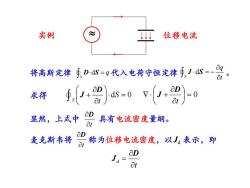
实例位移电流aqJ.ds:Φ.D·dS=q代入电荷守恒定律将高斯定律ataDaD0V求得dS=0atataD显然，上式中具有电流密度量纲。ataD麦克斯韦将称为位移电流密度，以J。表示，即ataDJdat

显然，上式中 具有电流密度量纲。 t D 位移电流 将高斯定律 代入电荷守恒定律 S d 。 q t   = −   d J S S  = q  D S t  = D Jd 麦克斯韦将 称为位移电流密度，以Jd 表示，即 t D d 0 S S t      +  =     D J  = 0          + t D 求得 J 实例 

Φ.(J+J).ds = 0V.(J+Ja)=0那么，求得上式称为全电流连续性原理。它包括了传导电流，运流电流及位移电流。由上可见，位移电流密度是电通密度的时间变化率，或者说是电场的时间变化率。aD在静电场中，由于三0，自然不存在位移电流。at在时变电场中，电场变化愈快，产生的位移电流密度也愈大。已知传导电流密度J=E，那么J。=0在理想介质（α=0)中J>Ja在良导体中

d ( ) d 0 S +  =  那么，求得 J J S (J + Jd ) = 0 上式称为全电流连续性原理。它包括了传导电流， 运流电流及位移电流。 由上可见，位移电流密度是电通密度的时间变化 率，或者说是电场的时间变化率。 在静电场中，由于 = 0 ，自然不存在位移电流。   t D 在时变电场中，电场变化愈快，产生的位移电流 密度也愈大。 在良导体中 J J c d  已知传导电流密度 Jc = E ，那么 在电导率较低的介质中 J J c d  位移电流 c 在理想介质 ( 0)  = 中 J = 0

麦克斯韦认为位移电流也可产生磁场，因此前述的安培环路定律变为$, H .dl = J,J ds → ,H dl= J,(U+J) dsaD, H-dl =J,(+),dsVxH=J+即atat上两式称为全电流定律。它表明，时变磁场是由传导电流，运流电流以及位移电流共同产生的。位移电流是由时变电场形成的，由此可见，时变电场可以产生时变磁场。电磁感应定律表明，时变磁场可以产生时变电场。因此，麦克斯韦引入位移电流概念以后，预见时变电场与时变磁场相互转化的特性可能会在空间形成电磁波。这一英明预见，后来在1888年被德国学者赫兹的实验所证实

d ( ) d l S t   = +     D H l J S t   = + D 即 H J 上两式称为全电流定律。它表明，时变磁场是由传导 电流，运流电流以及位移电流共同产生的。 位移电流是由时变电场形成的，由此可见，时变电 场可以产生时变磁场。 电磁感应定律表明，时变磁场可以产生时变电场。 因此，麦克斯韦引入位移电流概念以后，预见时变电 场与时变磁场相互转化的特性可能会在空间形成电磁 波。这一英明预见，后来在1888年被德国学者赫兹的实 验所证实。 麦克斯韦认为位移电流也可产生磁场，因此前述 的安培环路定律变为 d d ( ) d l S  = +  d d   H l J J S l S  =    H l J S

处于信息时代的今天，从婴儿监视器到各种遥控设备、从雷达到微波炉、从地面广播电视到太空卫星广播电视、从地面移动通信到宇宙星际通信、从室外无线局域网到室内蓝牙技术、以及全球卫星定位导航系统等，无不利用电磁波作为信息载体。无线信息高速公路使人们能在任何地点、任何时间同任何人取得联系。电磁波还能制造一种身在远方的感觉，形成无线虚拟现实。目前中国已有四亿多网民，七亿多手机用户

处于信息时代的今天，从婴儿监视器到各种遥 控设备、从雷达到微波炉、从地面广播电视到太空 卫星广播电视、从地面移动通信到宇宙星际通信、 从室外无线局域网到室内蓝牙技术、以及全球卫星 定位导航系统等，无不利用电磁波作为信息载体。 无线信息高速公路使人们能在任何地点、任何时 间同任何人取得联系。电磁波还能制造一种身在远 方的感觉，形成无线虚拟现实。 目前中国已有四亿多网民，七亿多手机用户

HertzMaxwell1831-18791857-1894电磁波的广泛应用，充分地显示了19世纪的麦克斯韦和赫兹对于人类文明和进步的伟大贡献

Maxwell Hertz 电磁波的广泛应用，充分地显示了19世纪的 麦克斯韦和赫兹对于人类文明和进步的伟大贡献。 1831-1879 1857-1894

llono6Marconi俄国波波夫意大利马可尼(1859~1906)(1874～1937)

意大利马可尼 ( 1874～1937) Marconi 俄国波波夫 (1859～1906) Попов

7-2麦克斯韦方程静态场中的高斯定理及磁通连续性原理对于时变电磁场仍然成立。那么，对于时变电磁场，麦克斯韦归纳为四个方程，其积分形式和微分形式分别如下：积分形式微分形式aDaDH.dl =(J.dsVxH=J+全电流定律atataBcaBE.dl:一.dsVxE=电磁感应定律JsatatΦ B.ds= 0V.B=0磁通连续性原理Sd, D.dS=qV.D=p高斯定律

7-2 麦克斯韦方程 静态场中的高斯定理及磁通连续性原理对于时变电磁 场仍然成立。那么，对于时变电磁场，麦克斯韦归纳为 四个方程，其积分形式和微分形式分别如下： d ( ) d l S t   = +     D H l J S d d l S t   = −     B E l S d 0 S  =  B S d S  = q  D S 积分形式 t   = + D H J t    = − B E B = 0   D =  微分形式 全电流定律 电磁感应定律 磁通连续性原理 高斯定律

积分形式微分形式aDaD, H.dl = .(J+).dsVxH=J++atataBaBΦ E.dl =-{dsVxE=s atat$, B-dS =0V.B=0d, D.dS=qV.D=p可见，时变电场是有旋有散的，时变磁场是有旋无散的。但是，时变电磁场中的电场与磁场是不可分割的，因此，时变电磁场是有旋有散场在无源区中，时变电磁场是有旋无散的。电场线与磁场线相互交链，自行闭合，从而在空间形成电磁波。时变电场的方向与时变磁场的方向处处相互垂直

可见，时变电场是有旋有散的，时变磁场是有旋无 散的。但是，时变电磁场中的电场与磁场是不可分割 的，因此，时变电磁场是有旋有散场。 在无源区中，时变电磁场是有旋无散的。 电场线与磁场线相互交链，自行闭合，从而在 空间形成电磁波。 时变电场的方向与时变磁场的方向处处相互垂直。 d ( ) d l S t   = +     D H l J S d d l S t   = −     B E l S d 0 S  =  B S d S  = q  D S 积分形式 t   = + D H J t    = − B E B = 0   D =  微分形式