《大学物理实验》课程教案讲义（下）第四章 综合实验

第四章综合实验实验十四空气中声速测量频率介于20Hz~20KHz的机械波振动在弹性介质中的传播就形成声波，介于20KHz~500MHz的称为超声波，超声波的传播速度就是声波的传播速度，而超声波具有波长短、易于定向发射和汇聚等优点，声速实验所采用的声波频率一般都在20KHz~60KHz之间。在此频率范围内，采用压电陶瓷换能器作为声波的发射器和接收器效果最佳。【实验目的】1.了解超声波的产生、发射和接收的方法。2.通过实验了解压电陶瓷传感器的功能。3.进一步掌握示波器和信号发生器的使用。4.用共振干涉法、相位比较法测量声速，并加深对有关共振、振动合成、波的干涉等理论知识的理解。【实验仪器】SV-DH系列声速测试仪、示波器、声速测试仪信号源示波器声速测定仪信号发生器图4-14-1声速测定用实验仪器SV-DH系列声速测试仪的主要结构为超声波换能器（发射换能器、接收换能

第四章 综合实验 实验十四 空气中声速测量 频率介于 20Hz~20KHz 的机械波振动在弹性介质中的传播就形成声波，介于 20 KHz~500MHz 的称为超声波，超声波的传播速度就是声波的传播速度，而超 声波具有波长短、易于定向发射和汇聚等优点，声速实验所采用的声波频率一般 都在 20 KHz~60 KHz 之间。在此频率范围内，采用压电陶瓷换能器作为声波的 发射器和接收器效果最佳。 【实验目的】 1. 了解超声波的产生、发射和接收的方法。 2. 通过实验了解压电陶瓷传感器的功能。 3. 进一步掌握示波器和信号发生器的使用。 4. 用共振干涉法、相位比较法测量声速，并加深对有关共振、振动合成、波 的干涉等理论知识的理解。 【实验仪器】 SV-DH 系列声速测试仪、示波器、声速测试仪信号源 图 4-14-1 声速测定用实验仪器 SV-DH 系列声速测试仪的主要结构为超声波换能器(发射换能器、接收换能

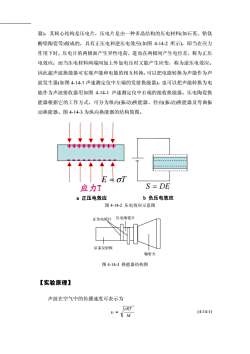
器），其核心结构是压电片，压电片是由一种多晶结构的压电材料（如石英、锆钛酸铅陶瓷等)做成的，具有正压电和逆压电效应(如图4-14-2所示)，即当在应力作用下时，压电片的两极面产生异性电荷，进而在两极间产生电位差，称为正压电效应：而当压电材料两端间加上外加电压时又能产生应变，称为逆压电效应。因此超声波换能器可实现声能和电能的相互转换，可以把电能转换为声能作为声波发生器(如图4-14-1声速测定仪中左端的发射换能器)，也可以把声能转换为电能作为声波接收器用如图4-14-1声速测定仪中右端的接收换能器。压电陶瓷换能器根据它的工作方式，可分为纵向（振动）换能器、径向（振动）换能器及弯曲振动换能器。图4-14-3为纵向换能器的结构简图。EoTS= DE应力Ta正压电效应b负压电效应图4-14-2压电效应示意图压电陶瓷片正负电极片后盖反射板辐射头图4-14-3换能器结构图【实验原理】声波在空气中的传播速度可表示为rRT(4-14-1)M

器)，其核心结构是压电片，压电片是由一种多晶结构的压电材料(如石英、锆钛 酸铅陶瓷等)做成的，具有正压电和逆压电效应(如图 4-14-2 所示)，即当在应力 作用下时，压电片的两极面产生异性电荷，进而在两极间产生电位差，称为正压 电效应；而当压电材料两端间加上外加电压时又能产生应变，称为逆压电效应。 因此超声波换能器可实现声能和电能的相互转换，可以把电能转换为声能作为声 波发生器(如图 4-14-1 声速测定仪中左端的发射换能器)，也可以把声能转换为电 能作为声波接收器用如图 4-14-1 声速测定仪中右端的接收换能器。压电陶瓷换 能器根据它的工作方式，可分为纵向(振动)换能器、径向(振动)换能器及弯曲振 动换能器。图 4-14-3 为纵向换能器的结构简图。 应力T a 正压电效应 ++++++++++ - - - - - - - - - - = σTE = DES b 负压电效应 图 4-14-2 压电效应示意图 辐射头 正负电极片 压电陶瓷片 后盖反射板 图 4-14-3 换能器结构图 【实验原理】 声波在空气中的传播速度可表示为 M rRT υ = (4-14-1)

式式4-14-1中r是空气定压比热容和定容比热容之比(r=C,/C），R是普适气体常数，M是气体的摩尔质量，T是热力学温度。从式4-14-1式可以看出，温度是影响空气中声速的主要因素。如果忽略空气中水蒸汽和其他杂质的影响，在0rRT.=331.45Do=M℃(T。=273.15)时的声速m/st℃时的声速可表示为tD, = Vo /1+ 273.15(4-14-2)由波动理论知道，波的频率f、波速D和波长入之间有以下关系D= fa(4-14-3)所以只要知道频率和波长就可以求出波速。本实验用信号发生器控制换能器，故信号发生器的输出频率就是声波的频率。而声波的波长可以用共振干涉法(驻波法)、行波法（相位比较法)来进行测量。1.共振干涉法(驻波法)测量波长实验装置接线如图4-14-4所示，图中S1和S2为压电陶瓷超声换能器。S1作为超声源（如图4-14-1b中的发射换能器），信号发生器输出的正弦交变电压信号接到换能器S1上，使S1发出一平面波，且沿X方向传播。S2作为超声波接收器（如图4-14-1b中的接收换能器），把接收到的声压转换成交变的正弦电压信号后输入示波器观察，同时S2还反射一部分超声波，这样，入射波和反射波叠加，因两列波具有相同的振幅A、相同的频率f和波长入，在X轴方向上以相反的方向传播，它们的波动方程分别为y=Acos2元(ft-(4-14-4)A2 = Acos[2元(f+)+ 元](4-14-5)元入射波与反射波叠加后的方程以及声压方程为y=+2=(2Asin2元)sin2f(4-14-6)元2元P= p(ux -ux)= py (μ_二) 4fpvAcos2xsin2元ft(4-14-7)dt两波合成后，介质中各点都在作同频率的简谐振动，各点的振幅为

式式 4-14-1 中 r 是空气定压比热容和定容比热容之比( = CCr Vp )，R 是普适气 体常数，M 是气体的摩尔质量，T 是热力学温度。从式 4-14-1 式可以看出，温度 是影响空气中声速的主要因素。如果忽略空气中水蒸汽和其他杂质的影响，在 0 ℃( )时的声速 T0 = 15.273 45.331 0 0 == M rRT υ m/s t℃时的声速可表示为 15.273 1 0 t t υυ += (4-14-2) 由波动理论知道，波的频率 、波速 f υ 和波长λ 之间有以下关系 υ = fλ (4-14-3) 所以只要知道频率和波长就可以求出波速。本实验用信号发生器控制换能 器，故信号发生器的输出频率就是声波的频率。而声波的波长可以用共振干涉法 (驻波法)、行波法(相位比较法)来进行测量。 1. 共振干涉法(驻波法)测量波长 实验装置接线如图 4-14-4 所示，图中 S1 和 S2 为压电陶瓷超声换能器。S1 作为超声源(如图 4-14-1b 中的发射换能器)，信号发生器输出的正弦交变电压信 号接到换能器 S1 上，使 S1 发出一平面波，且沿 X 方向传播。S2 作为超声波接 收器(如图 4-14-1b 中的接收换能器)，把接收到的声压转换成交变的正弦电压信 号后输入示波器观察，同时 S2 还反射一部分超声波，这样，入射波和反射波叠 加，因两列波具有相同的振幅 A、相同的频率 和波长 f λ ，在 X 轴方向上以相反 的方向传播，它们的波动方程分别为： )(2cos 1 λ π x = ftAy − (4-14-4) ])(2cos[ 2 π λ = π ++ x ftAy (4-14-5) 入射波与反射波叠加后的方程以及声压方程为 ft x Ayyy π λ π 2sin)2sin2( 21 =+= (4-14-6) ftxvAf dt yyd vuuvp π λ π ρ ρ ρπ 2sin 2 cos4 )( )( 21 = − 入 反 =−= (4-14-7) 两波合成后，介质中各点都在作同频率的简谐振动，各点的振幅为

L与时间无关，是位置的函数，对应于sin2元2Asin2元=1的各点振幅最大，元元X称为波腹，对应于sin2元=0的各点振幅最小，称为波节。而声压则正相反，A介质中各点的波腹位置对应于声压的波节位置，波节位置对应于声压的波腹位x置。要使sin2元=0，应有a2=±n元,n=0,1,2,3,.(4-14-8)17因此在x=(n=0,1,2,3)处就是波节的位置，相邻两波节间的距离为+n2(半波长)。同理，x=±(2n+1)(n=0,1,2,3,.)处就是波腹的位置，相邻两波2腹间的距离也为二2发送器S1接收器S2XH-2信号发生器频率显示广0声速测量仪幅度调节电源开关频率调节正弦波信号?CCO信号编细调相调图4-14-4实验装置接线图当形成驻波时，由于发射换能器S1、接收换能器S2作为固定端处在波节4位置，声压则为波腹位置，因此，它们之间的距离为L=n(n=0,1,2,3,..)，相2应的由声压引起的正压电效应越强，接收换能器的压电片间电压越大。故而在示波器中观察到的信号振幅越大。2.行波法(相位比较法)测量波长。实验装置接线仍如图2所示，示波器功能档置于X-Y方式。当S1发出的平面超声波通过媒质到达接收器S2，在发射波和接收波之间产生相位差：L1=2f-(4-14-9)0=-2=2元-1V因此可以通过测量?来求得声速

λ π x A 2sin2 ，与时间无关，是位置的函数，对应于 = 12sin λ π x 的各点振幅最大， 称为波腹，对应于 = 02sin λ π x 的各点振幅最小，称为波节。而声压则正相反， 介质中各点的波腹位置对应于声压的波节位置，波节位置对应于声压的波腹位 置。要使 = 02sin λ π x ，应有 2 nn =±= ,3,2,1,0 L x π， λ π (4-14-8) 因此在 ),3,2,1,0( 2 nnx =±= L λ 处就是波节的位置，相邻两波节间的距离为 2 λ (半波长)。同理， ),3,2,1,0( 2 )12( nnx =+±= L λ 处就是波腹的位置，相邻两波 腹间的距离也为 2 λ 。 图 4-14-4 实验装置接线图 当形成驻波时，由于发射换能器 S1、接收换能器 S2 作为固定端处在波节 位置，声压则为波腹位置，因此，它们之间的距离为 ),3,2,1,0( 2 nnL == L λ ，相 应的由声压引起的正压电效应越强，接收换能器的压电片间电压越大。故而在 示波器中观察到的信号振幅越大。 2. 行波法(相位比较法)测量波长。 实验装置接线仍如图 2 所示，示波器功能档置于 X-Y 方式。当 S1 发出的平 面超声波通过媒质到达接收器 S2，在发射波和接收波之间产生相位差： ν π λ πϕϕϕ L f L 21 ==−=Δ 22 (4-14-9) 因此可以通过测量Δϕ 来求得声速。 XH-2 信号发生器 幅度调节 电源开关 频率调节 频率显示 功率输出 信号输出 细调 粗调 Hz X Y 正弦波信号 示波器 声速测量仪 发送器S1 接收器S2

Aβ的测定可用相互垂直振动合成的李萨如图形来进行，设输入X轴的入射波振动方程为：x = A, cos(wt+p)(4-14-10)输入Y轴的是由S2接收到的波动，其振动方程为：y= A, cos(wt+@2)(4-14-11)上两式中A和A2分别为X、Y方向振动的振幅，W为角频率，9和β,分别为X、Y方向振动的初位相，则合成振动方程为：+cos(02-01)=sin (02-0)(4-14-12)AAAA,此方程轨迹为椭圆，椭圆长、短轴和方位由相位差△=2-,来决定。当Ag=0时，由式4-14-12得y=4x，即轨迹为处于第一和第三象限的一条直线，A显然直线的斜率为，如图4-14-5(=0)所示；当A=元时，得y=-x，则AA,轨迹为处于第二和第四象限的一条直线，如图4-14-5(Φ=元）所示。改变S:和S2之间的距离L，相当于改变了发射波和接收波之间的相位差，示波器显示屏上的图形也随L不断变化。显然，当S1和S2之间距离改变半个波长△L=入/2，则△改变了元，随之振动的位相差经历了从0～元的变化，李萨如图形从斜率为正的直线变为椭圆，再变到斜率为负的直线。因此，每重复出现斜率符号相反的直线，就意味着移动半个波长，进而测得波长入和频率f，根据=f可计算出室温下声波在媒质中传播的速度。ONAHβ=00=元/29=3元/20=2元0=元图4-14-5李萨如图形与两垂直简谐运动的相位差

Δϕ 的测定可用相互垂直振动合成的李萨如图形来进行，设输入 X 轴的入射 波振动方程为： )cos( = 1 wtAx +ϕ1 (4-14-10) 输入 Y 轴的是由 S2 接收到的波动，其振动方程为： )cos( = 2 wtAy +ϕ 2 (4-14-11) 上两式中A1和A2分别为X、Y方向振动的振幅，w为角频率，ϕ1和ϕ2 分别为 X、Y方向振动的初位相，则合成振动方程为： )(sin)cos( 2 12 2 12 21 2 2 2 2 1 2 −+ −=− ϕϕϕϕ AA xy A y A x (4-14-12) 此方程轨迹为椭圆，椭圆长、短轴和方位由相位差Δϕ = ϕ −ϕ12 来决定。当 Δϕ =0 时，由式 4-14-12 得 x A A y 1 2 = ，即轨迹为处于第一和第三象限的一条直线， 显然直线的斜率为 1 2 A A ，如图 4-14-5(ϕ =0)所示；当Δϕ = π 时，得 x A A y 1 2 −= ，则 轨迹为处于第二和第四象限的一条直线，如图 4-14-5(ϕ =π )所示。 改变S1和S2之间的距离L，相当于改变了发射波和接收波之间的相位差，示 波器显示屏上的图形也随L不断变化。显然，当S1 和S2 之间距离改变半个波长 L =Δ λ 2 ，则Δϕ 改变了π ，随之振动的位相差经历了从 0~π 的变化，李萨如图 形从斜率为正的直线变为椭圆，再变到斜率为负的直线。因此，每重复出现斜率 符号相反的直线，就意味着移动半个波长，进而测得波长λ 和频率f，根据υ = λf 可计算出室温下声波在媒质中传播的速度。 ϕ = 0 ϕ = π 2/ ϕ = π ϕ = π 2/3 ϕ = 2π 图 4-14-5 李萨如图形与两垂直简谐运动的相位差

【实验内容】(一)声速测定仪系统的连接如图4-14-4所示连接好电路，在实验之前，将信号发生器的频率换档开关打向上（频率换档的钮子开关打向上，频率显示范围为1200Hz~100KHz，钮子开关打向下，频率显示范围为20Hz~1600Hz)，信号发生器和示波器开机预热15分钟，选择介质为空气的初始状态。并观测S1及S2是否平行。（二）测定压电陶瓷换能器系统的最佳工作频率只有当换能器S1和S2发射面与接收面保持平行时才有较好的接收效果：为了得到较清晰的接收波形，应将外加的驱动信号频率调节到发射换能器S1谐振频率点（约37KHz)处，才能较好地进行声能与电能的相互转化，提高测量精度，以得到较好的实验效果。(三)用共振干涉法(驻波法)测量波长和声速1.按图4-14-4所示连接好电路。2.将测量方法设置到连续波方式，把声速测定仪信号发生器调到最佳工作频率，在共振频率下，将S2移近S1处，缓慢移离S2，当示波器上出现最大振幅时，记下读数标尺位置X。3.依次移动S2，记下各振幅最大时的X2，X3共12个值。4.记下室温t。5.用逐差法处理数据。（四）用相位比较法（李萨如图形）测量波长1.将测量方法设置到连续波方式，连接好电路，把声速测定仪信号发生器调到最佳工作频率，将示波器调至信号合成状态，即示波器上的TIME/DIV旋钮置于X-Y方式，移动S2轻轻靠拢S1，然后缓慢移开S2，观察示波器出现的李萨如图形3(=0)，记下位置X。2.依次移动S2，记下示波器的波形由图1(0=0)变为图3(=元）时，读数标尺位置的读数X2”，X3共12个值。3.记下室温t。4.用逐差法处理数据

【实验内容】 (一)声速测定仪系统的连接 如图 4-14-4 所示连接好电路，在实验之前，将信号发生器的频率换档开关 打向上(频率换档的钮子开关打向上，频率显示范围为 1200Hz~100 KHz，钮子开 关打向下，频率显示范围为 20 Hz ~1600 Hz)，信号发生器和示波器开机预热 15 分钟，选择介质为空气的初始状态。并观测 S1 及 S2 是否平行。 (二)测定压电陶瓷换能器系统的最佳工作频率 只有当换能器 S1 和 S2 发射面与接收面保持平行时才有较好的接收效果； 为了得到较清晰的接收波形，应将外加的驱动信号频率调节到发射换能器 S1 谐 振频率点(约 37KHz)处，才能较好地进行声能与电能的相互转化，提高测量精度， 以得到较好的实验效果。 (三)用共振干涉法(驻波法)测量波长和声速 1. 按图 4-14-4 所示连接好电路。 2. 将测量方法设置到连续波方式，把声速测定仪信号发生器调到最佳工作 频率，在共振频率下，将S2 移近S1 处，缓慢移离S2，当示波器上出现最大振幅 时，记下读数标尺位置X1’。 3. 依次移动S2，记下各振幅最大时的X2’， X3’. 共 12 个值。 4. 记下室温 t。 5. 用逐差法处理数据。 (四)用相位比较法(李萨如图形)测量波长 1. 将测量方法设置到连续波方式，连接好电路，把声速测定仪信号发生器 调到最佳工作频率，将示波器调至信号合成状态，即示波器上的TIME/DIV旋钮 置于X-Y方式，移动S2 轻轻靠拢S1，然后缓慢移开S2，观察示波器出现的李萨 如图形 3(ϕ =0)，记下位置X1’。 2. 依次移动S2，记下示波器的波形由图 1(ϕ =0)变为图 3(ϕ =π )时，读数标 尺位置的读数X2’， X3’. 共 12 个值。 3. 记下室温 t。 4. 用逐差法处理数据

【注意事项】1.移动接收换能器时，请勿将其与发射换能器碰触，以免损坏内部的压电片。2．请勿将接收换能器移动到声速测定仪的最右端，以免被卡死，无法改变其位置。【数据记录】Hz表4-14-1声速测定数据记录表f=位置L位置L+（mm）(mm)A=(Li+6-L,) /3测量次数i测量次数计6172839410511612-/6U=f.π-=

【注意事项】 1. 移动接收换能器时，请勿将其与发射换能器碰触，以免损坏内部的压电片。 2. 请勿将接收换能器移动到声速测定仪的最右端，以免被卡死，无法改变其 位置。 【数据记录】 表 4-14-1 声速测定数据记录表 f = Hz 测量次数 i 位置 Li （mm） 测量次数 i+6 位置 Li+6 （mm） λ +6 −= iii /)LL( 3 1 7 2 8 3 9 4 10 5 11 6 12 = ∑ 6/ λλ i = f ⋅= λυ =

实验十五磁滞回线与磁化曲线的测量在交通、通讯、航天、自动化仪表等领域中，大量应用各种特性的铁磁材料。常用的铁磁材料多数是铁和其它金属元素或非金属元素组成的合金以及某些包含铁的氧化物（铁氧体）。铁磁材料的主要特性是磁导率u非常高，在同样的磁场强度下铁磁材料中磁感应强度要比真空或弱磁材料中的大几百至上万倍。磁滞回线和磁化曲线表征了磁性材料的基本磁化规律，反映了磁性材料的基本磁参数，对铁磁材料的应用和研制具有重要意义。在实用上及大学物理实验中都显得非常重要。【实验目的】1.学习待测磁性样品的退磁，测量样品的起始磁化曲线。2.在待测样品达到磁饱和时，进行磁锻炼，测量材料的磁滞回线。3.学习安培回路定律在磁测量中的应用。【实验仪器】FD-BH-I型磁性材料磁滞回线和磁化曲线测定仪，包括：数字式特斯拉计、恒流源（四位半LED显示，可调恒定电流0-600.0mA）、磁性材料样品三种（截面长2.00cm；宽2.00cm；隔隙2.00mm，具体参照图4-14-5中的数据）、磁化线圈总匝数N=2000。图4-15-1FD-BH-I型磁性材料磁滞回线和磁化曲线测定仪

实验十五 磁滞回线与磁化曲线的测量 在交通、通讯、航天、自动化仪表等领域中，大量应用各种特性的铁磁材料。 常用的铁磁材料多数是铁和其它金属元素或非金属元素组成的合金以及某些包 含铁的氧化物（铁氧体）。铁磁材料的主要特性是磁导率μ非常高，在同样的磁 场强度下铁磁材料中磁感应强度要比真空或弱磁材料中的大几百至上万倍。 磁滞回线和磁化曲线表征了磁性材料的基本磁化规律，反映了磁性材料的基 本磁参数，对铁磁材料的应用和研制具有重要意义。在实用上及大学物理实验中 都显得非常重要。 【实验目的】 1. 学习待测磁性样品的退磁，测量样品的起始磁化曲线。 2. 在待测样品达到磁饱和时，进行磁锻炼，测量材料的磁滞回线。 3. 学习安培回路定律在磁测量中的应用。 【实验仪器】 FD-BH-Ⅰ型磁性材料磁滞回线和磁化曲线测定仪，包括：数字式特斯拉计、 恒流源(四位半 LED 显示，可调恒定电流 0-600.0mA)、磁性材料样品三种(截面 长 2.00cm；宽 2.00cm；隔隙 2.00mm，具体参照图 4-14-5 中的数据)、磁化线圈 总匝数 N=2000。 图 4-15-1 FD-BH-Ⅰ型磁性材料磁滞回线和磁化曲线测定仪

【实验原理】（1）铁磁物质的初始磁化曲线和磁滞回线研究铁磁材料的磁化规律，一般是通过测量磁化场的磁场强度H与磁感应强度B之间的H关系来进行的。铁磁材料的磁化过程非常复杂，AB与H之间的关系如图4-15-2所示。当铁磁材图4-15-2初始磁化曲线和磁滞回线料从未磁化状态（H=0且B=0）开始磁化时，B随H的增加而非线性增加。当H增大到一定值H后，B增加十分缓慢或基本不再增加，这时磁化达到饱和状态，称为磁饱和。达到磁饱和时的H，和B分别称为饱和磁场强度和饱和磁感应强度（对应图4-15-2中Q点）。B~H曲线OabQ称为初始磁化曲线。当使H从Q点减小时，B也随之减小，但不沿原曲线返回，而是沿另一曲线QRD下降。当H逐步较小至0时，B不为0，而是Br，说明铁磁材料中仍然保留一定的磁性，这种现象称为磁滞效应，B,称为剩余磁感应强度，简称剩磁。要消除剩磁，必须加一反向的磁场，直到反向磁场强度H=-Hc，B才恢复为0，Hc称为矫顽力。继续反向增加H，曲线达到反向饱和（Q点），对应的饱和磁场强度为-H，，饱和磁感应强度为-Bm。再正向增大H，曲线回到起点Q。从铁磁材料的磁化过程可知，当磁化场H按H㎡→0→-Hc→-H→0Hc→H依次变化时，B所经历的相应变化依次为B.→B,→0→-Bm→-B,→0→Bm，这一过程形成的闭合B~H曲线称为磁滞回线。采用直流励磁电流产生磁化场对材料样品反复磁化测出的磁滞回线称为静态（直流）磁滞回线。（2）基本磁化曲线和磁导率未磁化状态的铁磁材料，在磁化场作用下由弱到强依次进行磁化的过程中，可以测出面积由小到大的一簇磁滞回线，如图4-15-3所示。这些磁滞回线顶点的连线叫做铁磁材料的基本磁化曲线。根据基本磁化曲线可以近似确定铁磁材料的图4-15-3一簇磁滞回线磁导率μ。从基本磁化曲线上一点到原点O连线

【实验原理】 （1）铁磁物质的初始磁化曲线和磁滞回线 研究铁磁材料的磁化规律，一般是通过测 量磁化场的磁场强度 H 与磁感应强度 B 之间的 关系来进行的。铁磁材料的磁化过程非常复杂， B 与 H 之间的关系如图 4-15-2 所示。当铁磁材 料从未磁化状态（H=0 且 B=0）开始磁化时， 随 B H 的增加而非线性增加。当 H 增大到一定值 后，B 增加十分缓慢或基本不 再增加，这时磁化达到饱和状态，称为磁饱和。达到磁饱和时的 和 分别称 为饱和磁场强度和饱和磁感应强度（对应图 4-15-2 中 Q 点）。B~H 曲线 OabQ 称 为初始磁化曲线。当使 Hm Hm Bm H 从 Q 点减小时， 也随之减小，但不沿原曲线返回， 而是沿另一曲线 QRD 下降。当 B H 逐步较小至 0 时，B 不为 0，而是 Br ，说明铁 磁材料中仍然保留一定的磁性，这种现象称为磁滞效应， 称为剩余磁感应强 度，简称剩磁。要消除剩磁，必须加一反向的磁场，直到反向磁场强度 Br H ＝ ， 才恢复为 0，Hc 称为矫顽力。继续反向增加 − Hc B H ，曲线达到反向饱和（Q'点）， 对应的饱和磁场强度为 ，饱和磁感应强度为 − Hm − Bm 。再正向增大 H ，曲线回 到起点 Q 。从铁磁材料的磁化过程可知，当磁化场 H 按 Hm →0→ → − Hc − Hm →0→Hc→ 依次变化时， 所经历的相应变化依次为 → →0→ →－ →0→ ，这一过程形成的闭合 B~H 曲线称为磁滞回 线。采用直流励磁电流产生磁化场对材料样品反复磁化测出的磁滞回线称为静态 （直流）磁滞回线。 Hm B Bm Br − Bm Br Bm 图 4-15-2 初始磁化曲线和磁滞回线 Q' Q 图 4-15-3 一簇磁滞回线 （2）基本磁化曲线和磁导率 未磁化状态的铁磁材料，在磁化场作用下由弱 到强依次进行磁化的过程中，可以测出面积由小到 大的一簇磁滞回线，如图 4-15-3 所示。这些磁滞 回线顶点的连线叫做铁磁材料的基本磁化曲线。 根据基本磁化曲线可以近似确定铁磁材料的 磁导率 μ 。从基本磁化曲线上一点到原点 O 连线

L行的斜率定义为该磁化状态下的磁导率B由于磁化曲线不是线性的，当Hu=H由O开始增加时，μ也逐步增加，然后达到一最大值。当H再增加时，由于磁感应强度达到饱和，u开始急剧减小，(0)H图4-15-4基本磁化曲线与μ~H如图4-15-4所示。磁导率u非常高是铁磁材料的主要特性，也是铁磁材料用途广泛的主要原因之一。2.磁化曲线和磁滞回线的测量在待测的铁磁材料样品上绕上一组磁化线圈，环形样品的磁路中开一极窄均匀间隙，间隙应尽可能小，磁化线圈中，在对磁化电流最大值1磁锻炼的基础上，对应每个磁化电流值，用数字式特斯拉计，测量间隙均匀磁场区中间部位的磁感应强度B，得到该磁性材料的磁滞回线。如图4-15-2中QRQRQ组成的曲线为磁滞回线，OQ曲线为材料的初始磁化曲线。对于一定大小的回线，磁化电流最大值设为Imo测量磁化曲线和磁滞回线要求：（1)测量初始磁化曲线或基本磁化曲线都必须由原始状态H=0，B=0开始：因此测量前必须对待测量样品进行退磁，以消除剩磁。（2）为了得到一个对称而稳定的磁滞回线，必须对样品进行反复磁化，即“磁锻炼”。在环形样品的磁化线圈中通过的电流为I，则磁化场的磁场强度H为NH=(4-15-1)N为磁化线圈的匝数，为样品平均磁路长度，单位为A/m用霍耳传感器测量铁芯材料初始磁化曲线和磁滞回线，由于铁芯是非闭合的，当铁芯在加外磁场被磁化的过程中，将在铁芯的两端产生自由磁极，其产生的磁场与磁化场的方向相反，故铁芯中的磁场强度并非为磁化场，必须进行修正：假设铁芯磁路中有1个小平行间隙l。，如图4-15-5，铁芯中平均磁路长度为e

的斜率定义为该磁化状态下的磁导率 H B μ = 。由于磁化曲线不是线性的，当 H 由 0 开始增加时， μ 也逐步增加，然后 达到一最大值。当 H 再增加时，由于磁 感应强度达到饱和， μ 开始急剧减小， 如图 4-15-4 所示。磁导率 μ 非常高是铁 磁材料的主要特性，也是铁磁材料用途广泛的主要原因之一。 μ 图 4 -15-4 基本磁化曲线与μ～ H μ 2.磁化曲线和磁滞回线的测量 在待测的铁磁材料样品上绕上一组磁化线圈，环形样品的磁路中开一极窄均 匀间隙，间隙应尽可能小，磁化线圈中，在对磁化电流最大值Im磁锻炼的基础上， 对应每个磁化电流Ik值，用数字式特斯拉计，测量间隙均匀磁场区中间部位的磁 感应强度 ，得到该磁性材料的磁滞回线。如图 B 4-15-2 中QRQ‘ R‘ Q组成的曲线 为磁滞回线，OQ曲线为材料的初始磁化曲线。对于一定大小的回线，磁化电流 最大值设为Im。 测量磁化曲线和磁滞回线要求： （1)测量初始磁化曲线或基本磁化曲线都必须由原始状态 H=0，B=0 开始， 因此测量前必须对待测量样品进行退磁，以消除剩磁。 （2)为了得到一个对称而稳定的磁滞回线，必须对样品进行反复磁化，即“磁 锻炼”。 在环形样品的磁化线圈中通过的电流为 I，则磁化场的磁场强度 H 为 I N l H = (4-15-1) N 为磁化线圈的匝数， l为样品平均磁路长度，单位为 A/m 用霍耳传感器测量铁芯材料初始磁化曲线和磁滞回线，由于铁芯是非闭合 的，当铁芯在加外磁场被磁化的过程中，将在铁芯的两端产生自由磁极，其产生 的磁场与磁化场的方向相反，故铁芯中的磁场强度并非为磁化场，必须进行修正： 假设铁芯磁路中有 1 个小平行间隙l g ，如图 4-15-5，铁芯中平均磁路长度为 l