《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第五章 恒定磁场

I2di,×(I,di, ×ar)μo.、安培力定律 dR24元Ho f idi ,xar二、比奥一—沙伐定律B,=R24元C2J(x',y,z)xarHoB(x,y,z) =R?4元VHo [j(t',y',z)xar ds"B(x,y,z)R24元s三、安培力F21=12dl,×BOF=F+F=q(vxB+E)四、洛仑兹办qv×B=q(i×B)
一、安培力定律 二、比奥——沙伐定律 B1= 四、洛仑兹力 三、安培力

五、磁感应强度的散度B()=>R4元V.(V× F)= 0则 .B=0六、磁感应强度的通量Φm=「B.dS七、磁通连续性原理$B.ds = 0S
五、磁感应强度的散度 dV R J r B r V ( ) 4 ( ) 0 B 0 F 则 ( ) 0 七、磁通连续性原理 六、磁感应强度的通量 s m B dS 0 S B dS
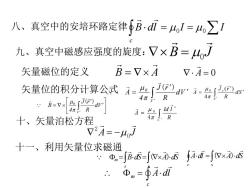
八、真空中的安培环路定律Bdi=o=I九、真空中磁感应强度的旋度:×B=uoB=V×A矢量磁位的定义V.A=0j(r)失量位的积分计算公式4=o0.2as4=dy4元RR4元/B=[[(avIdi'R4元:4oA=R4元十、矢量泊松方程V?A=-μoJ十一、利用矢量位求磁通+A-di -[(V×A)-dS @m={B.dS-{(VxA)-dsbA.dlΦ.一12
矢量位的积分计算公式 A 0 B A 矢量磁位的定义 九、真空中磁感应强度的旋度: B J 0 八、真空中的安培环路定律 B dl I I c 0 0 A dl A dS c s ( ) m c A dl 十一、利用矢量位求磁通 A J 0 2 十、矢量泊松方程 V 0 dV R J r 4 B ( ) S s dS R J r A ( ) 4 0 C R Id l A 4 0 V 0 dV R J r 4 A ( ) B dS A dS s s m ( )

磁矩Pm=IS十二、媒质的磁极子抗磁性媒质顺磁性媒质铁磁性媒质Zpm磁化强度M:M = limA/mAVAV->0A(F)=[xMMxi dsA(F)=HoPm ×RuodJ..=VxM4元R3RR4元4元Sj=MxnA()=av+ds4元R4元/R1:磁化体电流密度(束缚体电流);1磁化面电流密度(束缚面电流)
十二、媒质的磁磁化偶: 极子 磁矩 抗磁性媒质 顺磁性媒质 铁磁性媒质 磁化强度 M : A/m V p M m V O lim p m IS dS R J dV R J A r S sm V m 4 4 ( ) 0 0 : 磁化体电流密度(束缚体电流); sm : 磁化面电流密度(束缚面电流)。 m J J dS R M n dV R M A r V S 4 4 ( ) 0 0 J M n J M sm m 3 0 4 ( ) R p R A r m

H导磁媒质中的安培环路定律:B-di = μo(I+ I.) Im=Jmds-[(M)s =fM.diP(E-M).di = IF=(B磁场强度:A/m-M)uoo微分形式:VxH-J线性、各向同性媒质中,B.H.M之间的关系:M=xmHXm:磁化率B=(H+M)=%(+xm)HB= Hou,H =μHμr:相对磁导率
导磁媒质中的安培环路定律: ( ) 0 m c B d l I I s s m m I J dS M dS ( ) c M dl M dl I B c ( ) 0 ( ) 0 M B H H d l I c 磁场强度:A/m 微分形式: H J 线性、各向同性媒质中,B H M 之间的关系: . . M mH m :磁化率 B r H H 0 B H M m H 0( )0(1 ) r :相对磁导率

十三、恒定磁场的基本方程:1、磁通连续性原理:B.ds=0→ .B=0{H.di -I = VxH=J2、安培环路定律:3、磁场强度与磁感应强度的关系:H=(B-M) = B=M(H+M)oB=uH→M=XmH对于线性、各向同性媒质:V?A=-μj4、矢量磁位满足泊松方程:5、标量磁位满足拉普拉斯方程:dm=0 =(J=0)
3 、磁场强度与磁感应强度的关系: ( ) ( ) 0 M B H M B H 0 对于线性、各向同性媒质: B H M m H 4 、矢量磁位满足泊松方程: 0 ( ) 2 J 0 m A J 2 5 、标量磁位满足拉普拉斯方程: 十三、恒定磁场的基本方程: 1、磁通连续性原理: B dS B 0 s 0 2、安培环路定律: H dl I H J c

十四、不同媒质分界面上的边界条件:Bin = Bzn磁场的法向分量连续。切向分量关系:nx(H-H,)=JJ=0时,分界面上的,,与μ2之间的关系:nx(H,-H,)=0 → Hit=H2t[Bin= B2n [B, cos =B, cosd,H,= H2tH, sing = H, sing,tan0, -川.B=uHtan0,1l2
十四、不同媒质分界面上的边界条件: 磁场的法向分量连续。 B1n B2n 切向分量关系: s n H H J ( 1 2 ) Js 0 时,分界面上的 与 之间的关系: 1 2 2 . 1. 1 1 2 2 1 2 2 1 2 2 sin sin cos cos H H B B H H B B 1 t t 1n n B H 2 1 2 1 tan tan H H H1t H t n 1 2 2 ( ) 0

用位函数表示的分界面上的边界条件:当j。=0时,在分界面上的位函数为:n×(A, -A,)=0(4-70)i×(二V×A-1V×A,)=0uμ2ad0Φmlm2u2OnOn(4-71)DDm2
用位函数表示的分界面上的边界条件: ( ) 0 n A1 A2 ) 0 1 1 ( 2 2 1 1 n A A (4-70) 1 2 2 2 1 1 m m m m n n (4-71) 当 J s 0 时,在分界面上的位函数为:

dmi标量磁位单位:安(A)j=0 时 V×H=0 VxVΦ=0 ::H=-Vo[H.di=0mu-0mBUmAB =A、B两点间的磁压UmABma=[H.diA~B:积分路径不得穿越电流限定的面。40B标量磁位Φ满足拉普拉斯方程:Vo..=0V.(uH)=μV.H=μV.(-Vom)=0.V?0m=V.M非均匀磁化介质V·M0.V?...Psm =n.MV.M=-Pmm=-Pm4元JPdv+Psmds"gm(r)=4元RR4元V.MM.n14元JRR4元JS
标量磁位 m: 单位:安(A) J 0 时 H m H 0 0 标量磁位 m 满足拉普拉斯方程: A B mA H dl 0 A、B两点间的磁压 U mAB : mA mB B A mAB U H dl A~B:积分路径不得穿越电流限定的面。 0 m 2 ( ) ( ) 0 H H m 非均匀磁化介质

十五、电感L:自感:互感:内自感与外自感:@@Φ Φ 12L :LIM 121IiI2Φ,= Φ +Φ12 IΦ 22Φ 21M 2112IΦ2 = Φ 22 +Φ 2计算互感的一般公式:Φm2i=[B,r-dS= [(VxA.).dS= $Ar-dl,CCZ10.磁场能量:W,=)EdEZId-{H.BdVW.=21-1百:2;1H.B磁场的能量密度wm21LI2对于一个孤立的电流回路,其磁场能量为:Wm=22Wm1uH?dvL =则自感:1211
十五、电感 L: I L 2 22 22 1 11 11 I L I L 自感: 互感: 1 21 21 2 12 12 I M I M 内自感与外自感: 计算互感的一般公式: 2 2 2 21 21 21 2 ( ) C C C m21 B dS A dS A dl 2 22 21 1 11 12 磁场能量: i N i i N i m i i W I d I 1 1 1 0 2 1 V m W H BdV 2 1 w m H B 2 1 磁场的能量密度 则自感: V m H dV I I W L 2 2 2 2 1 对于一个孤立的电流回路,其磁场能量为: 2 2 1 W LI m
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第四章 恒定电流场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第三章 静电场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第二章 静电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第一章 矢量分析.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.1 库仑定律与电场强度 2.2 电位.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.3 静电 场中的导体与电介质.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.4 高斯通量定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.5 泊松方程和拉普拉斯方程.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.8 镜像法.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.6 分界面上的边界条件.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第四章 恒定磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.7 唯一性定理.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.9 导体系统的电容.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第二章 静电场 2.10 静电场能量、静电力.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第三章 恒定电场.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第五章 静态场的边值问题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)复习题题.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)第七章 平面电磁波.ppt
- 《电磁场与电磁能》课程PPT教学课件(马冰然版)总结复习.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第六章 电磁感应.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第七章 时变电磁场.ppt
- 《电磁场与电磁能》课程PPT教学课件(杨儒贵版)第八章 平面电磁波.pptx
- 《大学物理实验》课程教学大纲 Physics Experiment.pdf
- 《大学物理实验》课程教案讲义(上)物理实验绪论.pdf
- 《大学物理实验》课程教案讲义(上)第一章 测量与误差的基本知识.pdf
- 《大学物理实验》课程教案讲义(上)第二章 常用实验仪器简介.pdf
- 《大学物理实验》课程教案讲义(上)第三章 力学实验.pdf
- 《大学物理实验》课程教案讲义(上)第四章 光学实验.pdf
- 《大学物理实验》课程教案讲义(上)第五章 电学实验.pdf
- 《大学物理实验》课程教案讲义(下)第一章 力、热学实验.pdf
- 《大学物理实验》课程教案讲义(下)第三章 电磁学实验.pdf
- 《大学物理实验》课程教案讲义(下)第二章 光学实验.pdf
- 《大学物理实验》课程教案讲义(下)第五章 设计性实验.pdf
- 《大学物理实验》课程教案讲义(下)第四章 综合实验.pdf
- 《大学物理实验》课程教学课件(PPT讲稿)误差理论.ppt
- 《大学物理实验》课程教学课件(PPT讲稿)热学——导热系数测定.ppt
- 《大学物理实验》课程教学课件(PPT讲稿)热学——温度传感器.ppt
- 《大学物理实验》课程教学课件(PPT讲稿)热学——用混合法测固体比热容.ppt
- 《大学物理实验》课程教学课件(PPT讲稿)光学——分光计的调整实验.ppt
