《概率论与数理统计》课程教材课件（PPT讲稿）7-4 区间估计

第四节 区间估计 一、区间估计的基本概念 二、典型例题 三、小结

第四节 区间估计 一、区间估计的基本概念 二、典型例题 三、小结

、 区间估计的基本概念 1.置信区间的定义 设总体X的分布函数F(x9)含有一个未知参 数g,对于给定值a(0<a<1),若由样本X1,X2,L, X,确定的两个统计量 q=q(X1,X2,L,Xm)和4=q(X1,X2,L,Xm)满足 P{q(X1,X2,L,Xm)<9<q(X1,X2,L,Xn)}=1-M, 则称随机区间(g,9)是q的置信度为1-a的置信区 间，q和q分别称为置信度为1-a的双侧置信区间 的置信下限和置信上限，1-a为置信度

一、区间估计的基本概念 1. 置信区间的定义

关于定义的说明 被估计的参数g虽然未知，但它是一个常数， 没有随机性，而区间(g,4)是随机的. 因此定义中下表达式 Pig(X,X2,L,X)<q<q(X,X2L,X)=1-a 的本质是： 随机区间g,q)以1-a的概率包含着参数q的真值， 而不能说参数g以1-a的概率落入随机区间g,9)

关于定义的说明

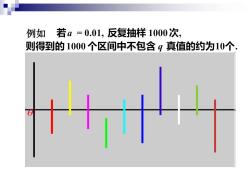
例如 若a=0.01,反复抽样1000次， 则得到的1000个区间中不包含g真值的约为10个

例如

2.求置信区间的一般步骤（共3步） (1)寻求一个样本X,X,L,X,的函数： Z=Z(X,X2L ,Xq) 其中仅包含待估参数g,并且Z的分布已知 且不依赖于任何未知参数（包括q). (2)对于给定的置信度1-a,定出两个常数，b, Pfa<Z(X,X2,L,Xiq)<b=1-a

2. 求置信区间的一般步骤(共3步)

(3)若能从a<Z(X1,X2,L,Xm9)<b得到等价的 不等式q<q<q,其中g=q(X1,X2,L,Xm), 9=q(X1,X2L,Xm)都是统计量，那么(g,q)就 是g的一个置信度为1-a的置信区间

二、典型例题 例1设X1,X2,L,Xn是来自正态总体N(ms2) 的样本，其中s2为已知，m为未知，求的置信水平 为1-a的置信区间. 解因为X是m的无偏估计， 且U=X:mNO,1, s In X-m~N(0,1)是不依赖于任何未知参数的， s /n

解 例1 二、典型例题

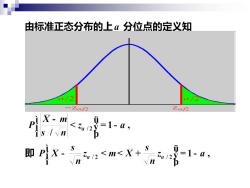
由标准正态分布的上a分位点的定义知 =1-4, 即PX.na<m<X+ a12 =1-a, n

于是得的一个置信水平为1-a的置信区间 0 3a12六 0 这样的置信区间常写成 0 a12 -/n 0 其置信区间的长度为2' n

这样的置信区间常写成 其置信区间的长度为

注意：置信水平为1-α的置信区间是不唯一的， 如果在例2中取n=16,s=1,=0.05, 查表可得n/2=3.25=1.96, 得一个置信水平为0.95的置信区间x±1‘1.969 16 0 由一个样本值算得样本均值的观察值x=5.20, 则置信区间为(5.20±0.49)，即(4.71,5.69)

由一个样本值算得样本均值的观察值 则置信区间为