《概率论与数理统计》课程教材课件（PPT讲稿，浙大版）第一章 概率论的基本概念 1.3 频率与概率

第三节频率与概率 讨论如何表征随机事件在一次试验中 发生的可能性的大小 频率 概率

第三节 频率与概率 ——讨论如何表征随机事件在一次试验中 发生的可能性的大小 频率 概率

一、频率 定义、在相同的条件下，进行了n次试验，在这n次试 验中，事件A发生的次数n,称为事件A发生的频数。比值 ”,n称为事件4发生的频率，并记成4.即④=元 基本性质： (⑩0≤f(A)≤1； (2)f(S)=1,f(②)=0； (3) 若A,A2,A是两两互不相容的事件，则 f(AUA2U.UA)=f(A)+f (A2)++(A) 说明：频率反映了在n次试验中，事件A发生的频繁程度； 频率越大，事件A在一次试验中发生的可能性就越大

定义 在相同的条件下，进行了 n 次试验，在这 n 次试 验中，事件 A 发生的次数nA 称为事件 A 发生的频数。比值 / n n A 称为事件 A 发生的频率，并记成 ( ) n f A 。 一、频率 (1) 0 ( ) 1; n   f A (2) ( ) 1, ( ) 0; f S f =  = (3) 若 1 2 , , , A A Ak是两两互不相容的事件，则 1 2 1 2 ( ) ( ) ( ) ( ) k n n n k f A A A f A f A f A = + + + 基本性质： 即 ( ) A n n f A n = 说明：频率反映了在n 次试验中，事件A发生的频繁程度； 频率越大，事件A在一次试验中发生的可能性就越大

实例将一枚硬币抛掷5次、50次、500次，各做 7遍，观察正面出现的次数及频率 试验 n=5 n=50 n=500 序号 na ng f ng f 1 2 0.4 22 0.44 251 0.502 产在1从h给士 0.498 3 随n的增大，频率f呈现出稳定性 U.4☑ Z50 0.512 4 5 0.50 247 0.494 5 1 在二处波动较心 0.502 波动最小 0.48 251 6 2 0.4 18 0.36 262 0.524 7 0.8 27 0.54 258 0.516

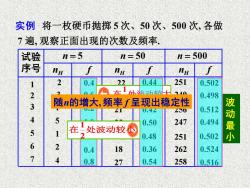
实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做 7 遍, 观察正面出现的次数及频率. 试验 序号 n = 5 nH f 1 2 3 4 5 6 7 2 3 1 5 1 2 4 nH f n = 50 22 25 21 25 24 18 27 nH n = 500 251 249 256 247 251 262 258 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.44 0.50 0.42 0.48 0.36 0.54 f 0.502 0.498 0.512 0.494 0.524 0.516 0.50 0.502 在 处波动较大 2 1 在 处波动较小 2 1 波 动 最 小 随n的增大, 频率 f 呈现出稳定性

实验者 n Hu f 德摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K皮尔逊 12000 6019 0.5016 K皮尔逊 24000 12012 0.5005 大量试验证实，当重复试验的次数n逐渐增大时，频率 f(A)呈现出稳定性，逐渐稳定于某个常数。 频率的性质 用频率表征事件A发生的可能性大小的缺点： (1)频率具有波动性，使得频率难以确定； 概率 (2)需要通过大量的重复试验才能求得：

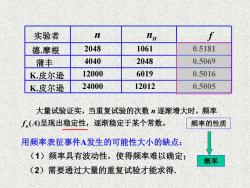
实验者 德.摩根 蒲丰 K.皮尔逊 K.皮尔逊 n nH f 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 大量试验证实，当重复试验的次数 n 逐渐增大时，频率 ( ) n f A 呈现出稳定性，逐渐稳定于某个常数。 用频率表征事件A发生的可能性大小的缺点： （1）频率具有波动性，使得频率难以确定； 频率的性质 概率 （2）需要通过大量的重复试验才能求得

二、概率 1933年，苏联数学家柯尔莫哥洛夫提出了概率论的公理化 结构，给出了概率的严格定义，使概率论有了迅速的发展。 Andrey Nikolaevich Kolmogorov (1903-1987)

二、概率 1933 年，苏联数学家柯尔莫哥洛夫提出了概率论的公理化 结构，给出了概率的严格定义，使概率论有了迅速的发展。 （1903 – 1987） Andrey Nikolaevich Kolmogorov

1.定义（概率的公理化） 设E是随机试验，S是它的样本空间.对于E的每一事件 A赋于一个实数，记为P(A),称为事件A的概率，如果集合 函数P()满足下列条件： (I)非负性：对于每一个事件A,有P(A)≥0； (2)规范性：对于必然事件S,有P(S)=1; (3)可列可加性：设A1,A,.是两两互不相容的事件， 即对于i≠j,A,A=0,i,j=1,2,则有 P(AUAU)=P(A)+P(4,)+. 概率的可列可加性

. , ( ) , ( ) : A E S E A P A P  设 是随机试验， 是它的样本空间 对于 的每一事件 赋于一个实数 记为 称为事件 的概 如果集合 函数 满 率 足下列条件 ， (1) 非负性：对于每一个事件 A P A ，有 ( ) 0  ; (2) 规范性：对于必然事件 S P S , ( ) 1; 有 = 1 2 , , , , , 1, 2, (3) i j A A i j A A i j  =  = 可列可加 设 是两两互不相容的事件， 即 于 性： 对 ，则有 1 2 1 2 P A A P A P A ( ) ( ) ( ) = + + 概率的可列可加性 1. 定义(概率的公理化)

2.性质 结合可列可加性，令 (1)P(0)=0. A1=A2=.=☑即可得证。 证明设A=☑(i=1,2,), 则UA=0,且A,A,=0,i≠j: 由概率的可列可加性得 P2,=Pg-24 =∑P(O) P(G)≥0 ncs

(1) ( ) 0. P  = 证明 ( 1,2, ), 设A i i =  = i 1 , , . i j i A A A i j  = 则 =  =   且 由概率的可列可加性得 1 ( ) i i P P A  =    =     1 ( )i i P A  = =  1 ( ) i P  = =   P( ) 0   P( ) 0.     =  2. 性质 结合可列可加性，令 A1 = A2 == 即可得证

(2)若A,A2,.,An是两两互不相容的事件，则有 P(4UAU.UA)=P(A)+PA)+.+P(4) 概率的有限可加性 证明令An+1=A+2=.=, →A1A=0,i≠j,i,j=1,2,. 由概率的可列可加性得 P4U4U-UA)-PUA)=2P4)=2P4)+0 =P(A)+P(A)+.+P(A)

概率的有限可加性 证明 1 2 , 令 A A n n + + = = =  , , , 1,2, .  =   = A A i j i j i j 由概率的可列可加性得 1 2 ( ) P A A An 1 ( ) k k P A  = = 1 ( ) k k P A  = =  1 ( ) 0 n k k P A = = +  1 2 ( ) ( ) ( ). P A P A P An = + + + 1 2 (2) , , , 若A A An是两两互不相容的事件，则有 1 2 1 2 ( ) ( ) ( ) ( ). P A A A P A P A P A n n = + + +

(3)设A,B为两个事件，且AcB,则 P(B-A)=P(B)-P(A);P(B)2P(A). 证明因为ACB, 所以B=AU(B-A). 又(B-A)∩A=O, P(B)=P(AU(B-A))=P(A)+P(B-A) 于是P(B-)=P(B)-P(A) 又因P(B-A)≥0， 故P(B)≥P(A)

(3) , , ( ) ( ) ( ) ( ) ( ). A B A B P B A P B P A P B P A  − = −  设 为两个事件，且 则 ； 证明 B 因为 A B  , 所以 B A B A = − ( ). 又 ( ) , B A A − =  又因 P B A ( ) 0, −  故 P B P A ( ) ( ).  于是 P B A P B P A ( ) ( ) ( ). − = − 得 P B P A B A P A P B A ( ) ( ( )) ( ) ( ) = − = + − A

常用关系式：ABCB; B-A=BA=B-AB. 推广P(B-A)=P(BA)=P(B)-P(AB) 对于任意事件A,B成立。 B B A A AB B

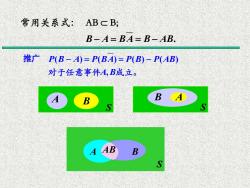
( ) ( ) ( ) ( ) , P B A P BA P B P AB A B − = = − 对于任意事件 成立。 推广 B A S S A B S A AB B 常用关系式： AB B; B A BA B AB.  − = = −