《基础化学》课程授课教案（物理化学讲义）第四章 溶液（Solution）

第四章溶液 (Solution)）(教案) 一、教学方案 1)理解拉乌尔定律与亨利定律 教学目的和 2)溶液中组分的化学势公式，明确标准态的选择；活度 要 与活度系数 3)掌握理想液态混合物的通性，稀溶液依数性公式推导 及计算 1)拉乌尔定律与亨利定律的正确理解与应用 教学重点 2)溶液中各组分的化学势及各个标准态的物理意义 3)活度与活度系数概念的理解与应用 4稀溶液依数性公式推导及计算 1)拉乌尔定律与立利定律的正确理解与应用 教学难点 2)溶液中各组分的化学势及各个标准态的物理意义 3)活度与活度系数概念的理解与应用 1)授课全部用多媒体电子教案，告别了传统的粉笔加黑 教学方法和手板的单一教学模式 2)辅导答疑采用电子邮件及在线论坛等模式 3)测验、考试的试卷由试题库自动组卷及试题分所。 1)§4-1引言 (0.5学时) 2)§42 容液的两个经验定律：(1.5学时) 教学内容及课 3)§4-3理想溶液的定义、通性及各组分的化学势：（① 时分配 学时) 4)§4-4稀溶液中各组分的化学势： (1学时) 5)S4-5稀溶液的依数性：(2学时) 6)§4-6非理想溶液(1学时)

第四章 溶液 (Solution) (教案) 一、教学方案 教学目的和 要求 1) 理解拉乌尔定律与亨利定律 2) 溶液中组分的化学势公式，明确标准态的选择；活度 与活度系数 3) 掌握理想液态混合物的通性，稀溶液依数性公式推导 及计算。 教学重点 1) 拉乌尔定律与亨利定律的正确理解与应用 2) 溶液中各组分的化学势及各个标准态的物理意义 3) 活度与活度系数概念的理解与应用 4) 稀溶液依数性公式推导及计算 教学难点 1) 拉乌尔定律与亨利定律的正确理解与应用 2) 溶液中各组分的化学势及各个标准态的物理意义 3) 活度与活度系数概念的理解与应用 教 学 方 法 和 手 段 1) 授课全部用多媒体电子教案，告别了传统的粉笔加黑 板的单一教学模式； 2) 辅导答疑采用电子邮件及在线论坛等模式; 3) 测验、考试的试卷由试题库自动组卷及试题分析。 教学内容及课 时分配 1) §4-1引言； (0.5学时) 2) §4-2 稀溶液的两个经验定律； (1.5学时) 3) §4-3理想溶液的定义、通性及各组分的化学势；(1 学时) 4) §4-4稀溶液中各组分的化学势； (1学时) 5) §4-5 稀溶液的依数性；(2学时) 6) §4-6 非理想溶液（1学时）

二、教案内容 §4.1引言 一、概念 通常米讲，溶即溶合，液即液相，两种以上的物质融合成为液相体系被成为溶液。如今， 我们 种种以上的纯物质所组成的均相体系。即以分子级程度相互分散的均相混 合体系称 组成溶 组分均相。溶液以物 购物质以分子分散程度相互混合，所以溶液的性质均匀，任何溶液都是多一 有 根据溶液中溶质的导电性又可分为电解质溶液和非电解质溶液。本章主要讨论液态的非电解 质溶液。关于电解质溶液，以后将专门讨论。 为了方便，我们将溶液中的一种物质叫做溶剂(solvent),通常A表示，而将其它物质叫 做溶质(solute),用B表示。溶质和溶剂只是一种人为的区分，有时两者并无严格界限。对于 气体或固体溶于某液体构成的溶液，习惯上将液体叫做溶剂，而将溶于其中的气体或周体叫 做溶质，如果是两种液体构成的溶液，则称其中量多的液体叫溶剂，量少的液体叫溶质。 二、溶液组成的习惯表示方法 作为由多种物质构成的均相系统 溶液的组成能够在一定范围内变化 成可变的系统。溶液的组成是溶 液系的状函精 成范围宽广，而且溶液的某些性质是随组成的不同而异。溶液组成的表示方法很多，最常用 的有以下四种： 1.物质的量分数（摩尔分数）溶液中物质B的物质的量分数定义为术B 物质B的质量/MB ∑（物质B的质量/MB) (4-1-1) 表示为物质B的物质的量与混合物的物质的量之比。此式中B不仅指溶质，而代表溶液中的任 ∑xB 一物质。显然 =1 2.质量分数物质B的质量分数是指溶液中所含B的质量与溶液的总质量之比：州： 物质B的质量 丁物质B的质量 WB B =1 (4-1-2) B和都是无量纲的量。” 3.溶质B的质量摩尔浓度(mlat)溶质B的质量摩尔浓度是指1Kg溶剂中所溶解的 B的物质的量：m店 ”_物质B的质量 mB_WA MBWA =NAMA (4-1-3) 式中为溶于质量为的溶剂A中的溶质B的物质的量：为溶剂A的摩尔质量，单位为

二、教案内容 §4.1 引 言 一、 概念 通常来讲，溶即溶合，液即液相，两种以上的物质融合成为液相体系被成为溶液。如今， 我们将其扩展重新定义： 凡是由二种或二种以上的纯物质所组成的均相体系，即以分子级程度相互分散的均相混 合体系称为溶液 （solution）。 由于组成溶液的物质以分子分散程度相互混合，所以溶液的性质均匀，任何溶液都是多 组分均相。溶液以物态可分为气态溶液、固态溶液和液态溶液。气体混合物是气态溶液，有 时在一定条件下多种不同的固体（例如Au和Ag）也可构成溶液，这种固态溶液称为固溶体。 根据溶液中溶质的导电性又可分为电解质溶液和非电解质溶液。本章主要讨论液态的非电解 质溶液。关于电解质溶液，以后将专门讨论。 为了方便，我们将溶液中的一种物质叫做溶剂(solvent)，通常A表示，而将其它物质叫 做溶质(solute)，用B表示。溶质和溶剂只是一种人为的区分，有时两者并无严格界限。对于 气体或固体溶于某液体构成的溶液，习惯上将液体叫做溶剂，而将溶于其中的气体或固体叫 做溶质，如果是两种液体构成的溶液，则称其中量多的液体叫溶剂，量少的液体叫溶质。 二、 溶液组成的习惯表示方法 作为由多种物质构成的均相系统，溶液的组成能够在一定范围内变化。因此，溶液是组 成可变的系统。溶液的组成是溶液系统的状态函数，是描述溶液的重要变量之一。溶液的组 成范围宽广，而且溶液的某些性质是随组成的不同而异。溶液组成的表示方法很多，最常用 的有以下四种： 1. 物质的量分数（摩尔分数） 溶液中物质B的物质的量分数定义为 = = （4-1-1） 表示为物质B的物质的量与混合物的物质的量之比。此式中B不仅指溶质，而代表溶液中的任 一物质。显然 =1 2. 质量分数 物质B的质量分数是指溶液中所含B的质量与溶液的总质量之比： = ； =1 （4-1-2） 和都是无量纲的量。 3. 溶质B的质量摩尔浓度（molaity） 溶质B的质量摩尔浓度是指1Kg溶剂中所溶解的 B的物质的量： = = （4-1-3） 式中为溶于质量为 的溶剂 A中的溶质 B的物质的量 ；为溶剂A的摩尔质量，单位为

K.l”形M,所以质量摩尔浓度的单位为m0lkgm'.对于二组分溶液，与的关系为： mxn 。 MA (4-1-4) 对于极稀的溶液，上式可以简化为 (4-1-5)xmMA 对于极稀的水溶液，有 xB=0.018mB 支，示组的方法。都是以质量为基准，因此成值不会随体积的流有品 A163 4.物质的量浓度(molarity)为每立方米溶液中所含有溶质B的物质的量C。 (4-1-7) 式中V是溶液的体积，单位为m,所以的单位为mol.m xp+(M.-M)c (4-1-8) MACB 对于极稀溶液，=x:P4 式中PA是溶剂的案度 浓度是溶液系统的强度性质，与溶液的量无关，这为同一溶液中各种不同标度的浓度之 Xmg3,B6山. C。 ma0.0177mol/0.9823·M-0.01770.9823*18*10)=1 moI.kg (2)取100g溶液，则其中含B为(4.4/46)mol,溶液体积为(0.1/992)m C=4.4/46/(0.1/992)=948m01.m §4.2稀溶液的两个经验定律 一、拉鸟尔定律(Raoult'slaw) 在大量实验的基础上，1887年R阳oult发现：在一定温度下，稀薄溶液中溶剂的蒸气压等 于纯溶剂的蒸气压乘以溶液中溶剂的物质的量分数，此结论称为Raoult定律，用公式表示为 (42-1)PP4x 式中代表纯溶剂A的蒸气压，代表溶液中溶剂的物质的量分数。P。x 如果溶液中只有A,B两个组分，则+1X产B

Kg.mol -1，所以质量摩尔浓度的单位为mol.kg -1 。对于二组分溶液，与的关系为： = （4-1-4） 对于极稀的溶液，上式可以简化为 = （4-1-5） 对于极稀的水溶液，有 =0.018 （4-1-6） 以上几种表示组成的方法，都是以质量为基准。因此组成值不会随体积的涨缩而有所改 变，与温度无关。 4. 物质的量浓度 (molarity): 为每立方米溶液中所含有溶质B的物质的量 = （4-1-7） 式中V是溶液的体积，单位为m 3 , 所以的单位为mol.m -3 . 对于二组分体系，与其它浓度单位关系 = （4-1-8） 对于极稀溶液，= = 式中 是溶剂的密度。 浓度是溶液系统的强度性质，与溶液的量无关，这为同一溶液中各种不同标度的浓度之 间进行换算提供了方便，只要取合适量的溶液就可进行简捷换算。 例3-1-1 （1）试求=0.0177的乙醇水溶液的质量摩尔浓度，（2）已知乙醇质量分数为0.044 的溶液的密度ρ=992kg.m -3 ,试求此水溶液的. 解：（1）取1mol溶液，则其中含B（即乙醇）和A（即水）分别为0.0177mol和0.9823mol. =0.0177mol/0.9823·M A =0.0177/(0.9823*18*10 -3 )=1mol.kg -1 (2) 取100g溶液，则其中含B为（4.4/46）mol, 溶液体积为(0.1/992)m 3 , =4.4/46/(0.1/992)=948mol.m-3 §4.2 稀溶液的两个经验定律 一、 拉乌尔定律（Raoult’s law） Raoult做了许多实验来测量溶液上方溶剂的蒸气压。将非挥发性溶质B溶于溶剂A中，溶 液上方与之平衡共存的蒸气的压力，即为溶剂气体的压力pA，可以直接由压力计读出。 在大量实验的基础上，1887年Raoult发现：在一定温度下，稀薄溶液中溶剂的蒸气压等 于纯溶剂的蒸气压乘以溶液中溶剂的物质的量分数，此结论称为Raoult定律，用公式表示为 = （4-2-1） 式中代表纯溶剂A的蒸气压，代表溶液中溶剂的物质的量分数。 如果溶液中只有A, B两个组分，则+=1

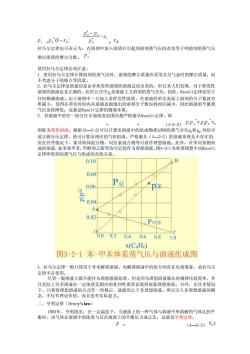
P.Pi(1-xs) 拉乌尔定律也可表示为：在溶剂中加入溶质后引起的溶剂蒸气压的改变等于纯溶剂的蒸气压 乘以溶质的摩尔分数。P 使用拉乌尔定律必须注意： 1.使用拉乌尔定律计算溶剂的燕气压时，溶剂的摩尔质量应采用其呈气态时的摩尔质最，而 不考虑分子的 但后来人们发现 式中P,是溶液上方溶剂的蒸气分压，因此，R 任何稀薄溶湾由于溶剂中 “旦加人非友性浴质，在溶液的单位表面上溶剂的分子数就有 寸间内从溶液表 的溶剂分子数也将相应减少，因此溶液的平衡蒸 将降低」 3. 律的 若溶液中的任组分在全部浓度范国内都严格服从Ra01t定律，即 4-2-1 PP.xPPs x。 则称为理想溶液。根据3一？-2)可以计算出溶液中的组成物质A和B的蒸气分压，和，再结合 但在有些 年多同 击的 如米和甲苯，甲醇和乙醇等均可近似作为理想洛液为理事系物 定律所得到的蒸气压与组成的直线关系 0.10 B 0.08 P点 0.06 p A d 0.02 。P甲苯 06002 0.40.60.81.0 x(C6H6) 图3-2-1苯-甲苯体系蒸气压与溶液组成图 4.拉乌尔定律一般只使用于非电解质溶液，电解质溶液中的组分因存在电离现象，故拉乌尔 定律不在使用 尽管一般溶液大都不能作为理想溶液处理，但是因为理想溶液服从的规律比较简单，并 且实际上许多溶液在 一定浓度范围内的某 吊衣 现得很 二、亨利定律(Henry'slaw) p= (4-2-3)kx

= = 拉乌尔定律也可表示为：在溶剂中加入溶质后引起的溶剂蒸气压的改变等于纯溶剂的蒸气压 乘以溶质的摩尔分数。 使用拉乌尔定律必须注意： 1. 使用拉乌尔定律计算溶剂的蒸气压时，溶剂的摩尔质量应采用其呈气态时的摩尔质量，而 不考虑分子的缔合等因素。 2. 拉乌尔定律虽然最初是由非挥发性溶质的溶液总结出来的，但后来人们发现，对于挥发性 溶质的溶液也是正确的，此时公式中pA是溶液上方溶剂的蒸气分压，因此，Raoult定律适用于 任何稀薄溶液。由于溶剂中一旦加入非挥发性溶质，在溶液的单位表面上溶剂的分子数就有 所减小，使得在单位时间内从溶液表面逸出的溶剂分子数也将相应减少，因此溶液的平衡蒸 气压也将降低。这就是Raoult定律的微观本质。 3. 若溶液中的任一组分在全部浓度范围内都严格服从Raoult定律，即 = = （4-2-2） 则称为理想溶液。根据(3— 2-2)可以计算出溶液中的组成物质A和B的蒸气分压pA和pB ,再结合 道尔顿分压定律，便可计算出相应的气相组成。严格服从（4— 2-2）的溶液系统是不存在的， 但在有些情况下，象异构体混合物、同位素混合物等可看作理想溶液。此外，许多同系物形 成的溶液，如苯和甲苯，甲醇和乙醇等均可近似作为理想溶液。图4-2-1为典型理想中由Raoult 定律所得到的蒸气压与组成的直线关系。 4. 拉乌尔定律一般只使用于非电解质溶液，电解质溶液中的组分因存在电离现象，故拉乌尔 定律不在使用。 尽管一般溶液大都不能作为理想溶液处理，但是因为理想溶液服从的规律比较简单，并 且实际上许多溶液在一定浓度范围内的某些性质常表现得很象理想溶液。另外，在许多情况 下，只要将理想溶液的公式作一些修正，就能用之于非理想溶液。所以引入非理想溶液的概 念，不仅有理论价值，而且也有实际意义。 二、亨利定律（Henry’s law） 1803年，亨利指出：在一定温度下，当液面上的一种气体与溶液中所溶解的气体达到平 衡时，该气体在溶液中的浓度与其在液面上的平衡压力成正比，这就是亨利定律。 = （4— 2-3）

上式中指所溶解气休在溶液面上的平衡压力，是该气体溶于溶液中的物质的量分数，为以 分数表示溶寝浓暖时的字利宿就，其数值决定于度·压力交溶质和溶剂 对于稀溶液，上式可以简化为 7: p=kx北，nB+na s北=大， 一记速海中所含洛质的物质的民，即等于溶的李东度，所式了 可以写为m上 p= (4-2-4)m 同理，在稀溶液中，若溶质的浓度用物质的量浓度表示，同样可得C。 （42-5)k.ca 太、均称为李利常数，为了使和与有相同的单位，我们将上述公式写做从，人人 州 其中m和。°分别表示标准质量摩尔浓度和标准物质的最浓度，习惯上取m=1mkg c=1000molm,这样和的单位均为Pa。显然以上几种亨利常数相互关联，可以互相换算。k,人 使用利 律时须 式的是该气体在液面上的分压力。对于混合气体在总压不太大的时候，亭利定律能 分别使用于每一种气体，可以近似地认为与其它气体的分压无关。 2.溶质在气相和在溶液中的分子状态必须是相同的，即溶液中溶质的浓度是与气相分子 状态相同的溶解态的浓度。如HC1,在气相为HC1分子，在液相为H,CI,则亨利定律不适 用 3.亨利定律一般只使用于稀溶液，当溶液浓度较高时，亨利定律会产生较大偏差，它是 ·个极限定律，溶液浓度越稀，对亨利定律符合愈好。对气休溶质，升高温度或降低压力， 降低了溶解度，能更好服从亨利定律。 三、两个定律之间的关系 相似点：都是从稀溶液中得出的规律：表示某一物质的平衡蒸气压与该组分在溶液中的浓度 成正比关系。 表4-2-1拉乌尔定律和亨利定律之间的差异 名称 表达式 研究对象 比例常数 代衣意义 拉乌尔定律P4=Px 溶剂 纯溶剂的蒸气压 亨利定律p=k,x 溶质为一实验值，没有明确的物理意义 §4.3理想溶液(ideal solution)的定义、通性及各组分的化学势 理想溶液的引入 的溶 求其共性，舍其差异。这就大大简化了科研中的困难，从而建立一套思想体系，在具体应用

上式中指所溶解气体在溶液面上的平衡压力， 是该气体溶于溶液中的物质的量分数，为以 物质的量分数表示溶液浓度时的亨利常数，其数值决定于温度、压力及溶质和溶剂的性质。 对于稀溶液，上式可以简化为 == 代表1.00kg溶剂中所含溶质的物质的量，即等于溶质的质量摩尔浓度（），所以上式又 可以写为 = （4— 2-4） 同理，在稀溶液中，若溶质的浓度用物质的量浓度表示，同样可得 = （4— 2-5） 、均称为亨利常数，为了使和与有相同的单位，我们将上述公式写做 = = 其中 和 分别表示标准质量摩尔浓度和标准物质的量浓度，习惯上取 =1mol.kg -1 , =1000mol.m -3 ，这样和的单位均为Pa。显然以上几种亨利常数相互关联，可以互相换算。 使用亨利定律时须注意下列几点： 1. 式中的是该气体在液面上的分压力。对于混合气体在总压不太大的时候，亨利定律能 分别使用于每一种气体，可以近似地认为与其它气体的分压无关。 2. 溶质在气相和在溶液中的分子状态必须是相同的，即溶液中溶质的浓度是与气相分子 状态相同的溶解态的浓度。如HCl,在气相为HCl分子，在液相为H + , Cl - ，则亨利定律不适 用。 3. 亨利定律一般只使用于稀溶液，当溶液浓度较高时，亨利定律会产生较大偏差，它是 一个极限定律，溶液浓度越稀，对亨利定律符合愈好。对气体溶质，升高温度或降低压力， 降低了溶解度，能更好服从亨利定律。 三、 两个定律之间的关系 相似点：都是从稀溶液中得出的规律；表示某一物质的平衡蒸气压与该组分在溶液中的浓度 成正比关系。 表4-2-1拉乌尔定律和亨利定律之间的差异 名称 表达式 研究对象 比例常数 代表意义 拉乌尔定律 = 溶剂 纯溶剂的蒸气压 亨利定律 = 溶质 为一实验值，没有明确的物理意义 §4.3 理想溶液（ideal solution）的定义、通性及各组分的化学势 一、 理想溶液的引入 理想溶液(ideal solution)，顾名思义，就是理想化的溶液，是实际不存在的溶液。科学 研究的前提往往是要首先建立一个理想化的模型，这个模型是从各种实际的溶液中抽出来的， 求其共性，舍其差异。这就大大简化了科研中的困难，从而建立一套思想体系，在具体应用

中加以修正，就可以用于实际体系，就完成了科研的全部内容，若一开始就考虑其方方面面， 我们将无从下手。 二、理想溶液的定义 宏观上：若溶液中的任一组分在全部浓度范围内都严格服从Raoulti定律的溶液。例如，A 和B形成理想溶液，测 =PP.x p. Paxa 各组分 小及作用力 分我千清义上的理想溶液只是一种抽象的型，实际是不存在的。但在实 际上，有许多体系都极接近于理想溶液。除了光学异构体的混合物，同位素化合物的混合物， 立体异构体的混合物以及紧邻同系物的混合物都可以近似算作理想溶液】 三、理想溶液中各组分的化学势 由于理想溶液溶质、溶剂没有独立的特征，只有量的差别，因此我们可以用同样的方法处 理混合物中的 首先讨论纯液体的化学势： 设温度T时，纯液体B与其蒸气平衡，根据化学势判据，B在气相和液相中的化学势必相等： (T.P)(T (4-3-1 式中是纯B在压力为P温度为 的平衡惑气压，P代表纯的化学势。 (4-3-2) 在上两式中消去，则得 (T.P)RTInP 若溶液服从拉乌尔定律=，代入上式得P,P。x。 -4g(红P)+RT1n (4-3-3)。 其中心（①，P)是温度T和压P时（即溶液上面的总压）纯B的化学势，这个态不是标准态， (8u 我们通常连用标准态的压力为P(101.325Pa,当外压改变时，化学势有所改变P,心 ,故积分得 i①，P)=n①+∫dp 4-3-0y 4(①)是标准态化学势。将(3-17)代入(3-16)得 %=。(T)+RTln+dp 43-5xJ 由于在通常情况下 P与标准压力P的偏差不会太大，且溶液体积受压力的影响很小，故若 忽略积分项，而认 店T,p)T.P)≈后T 3)或（1-3-51 理相

中加以修正，就可以用于实际体系，就完成了科研的全部内容，若一开始就考虑其方方面面， 我们将无从下手。 二、 理想溶液的定义 宏观上：若溶液中的任一组分在全部浓度范围内都严格服从Raoult定律的溶液。例如，A 和B形成理想溶液，则 = = 微观上：从分子模型上讲，各组分分子的大小及作用力，彼此相似，当一种组分的分子 被另一种组分的分子取代时，没有能量的变化或空间结构的变化。混合过程仅仅是几种物质 发生分子级大小的相互分散。 我们必须清楚，严格意义上的理想溶液只是一种抽象的模型，实际是不存在的，但在实 际上，有许多体系都极接近于理想溶液。除了光学异构体的混合物，同位素化合物的混合物， 立体异构体的混合物以及紧邻同系物的混合物都可以近似算作理想溶液。 三、 理想溶液中各组分的化学势 由于理想溶液溶质、溶剂没有独立的特征，只有量的差别，因此我们可以用同样的方法处 理混合物中的任一组分。 首先讨论纯液体的化学势： 设温度T时，纯液体B与其蒸气平衡，根据化学势判据，B在气相和液相中的化学势必相等： ∗B （T, P）= =(T)+ RTln (4-3-1) 式中是纯B在压力为P温度为T的平衡蒸气压， 代表纯B的化学势。 若溶液中有A, B同时存在，平衡时， = =(T)+ RTln （4-3-2） 在上两式中消去，则得 = （T, P）+ RTln 若溶液服从拉乌尔定律=，代入上式得 = （T, P）+ RTln （4— 3-3） 其中 （T, P）是温度T和压力P时（即溶液上面的总压）纯B的化学势，这个态不是标准态， 我们通常选用标准态的压力为 （101.325KPa），当外压改变时，化学势有所改变， =，故积分得 （T, P）= (T)+ ∫d p (4— 3-4) (T)是标准态化学势。将（3-17）代入（3-16）得 = (T)+ RTln+ d p （4-3-5） 由于在通常情况下，P与标准压力 的偏差不会太大，且溶液体积受压力的影响很小，故若 忽略积分项，而认为 （T, P）≈ (T, ) ≈ (T) 一般来说不致引起很大的误差。所以式（4-3-3）或（4-3-5）就是理想溶液中任一组分的化 学势的表示式。凡是溶液中任一组分的化学势在全部浓度范围内都能用这个公式表示者，则

该溶液就称为理想溶液或理想混合物，这就是理想溶液的热力学定义。 四、理想溶液的通性 由理想溶液模型和热力学定义式子可以推出理想溶液具有以下通性： 1.△=O,即由纯组分混合成溶液时，溶液的体积等于各组分的体积之和，而没有 额外的增加或减少。 1i.△0，这就是说在混合过程中，物质B的摩尔焓没有变化。所以混合前后总焓不 变，不产生热效应。 。具有理想的泥合桶4S三%血 iV.混合吉布斯自由能A.G。等温下，根据，△C=AHAS,应有△C=A.HA:S=RT, 由.所u2h526 .对于理想溶液，拉乌尔定律与亨利定律是没有区别的：=PP,x人， §4.4稀溶液中各组分的化学势 在理想稀溶液中，溶剂和溶质分别服从不同的规律，因此它们的化学势表示式具有不同 的具体内容，这是与理想溶液的不同之处。举二组分体系为例，A为溶剂，B为溶质。 1.稀溶液的定义 两种挥发性物质组成一溶液，在一定的温度和压力下，在一定的浓度范围内，溶剂遵守 拉乌尔定律，溶质遵守亨利定律，这种溶液称为稀溶液。值得注意的是，化学热力学中的稀 溶液并不仅仅是指浓度很稀的溶液。 2。溶剂的化学势 溶剂服从拉乌尔定律，其化学势应与理想溶液相同，即 (T)+RTIn X 3.溶质的化学势 在溶液中对于溶质而言， =A好=m+RTnP产 在稀溶液中溶质服从亨利定律，二。代入后得，P大， =①+RT1n大，P)+Tn, 女店≈①+n (4-4-1)x 其中4（①为标准态的化学势，可看作是在温度为，压力P,当=1，仍服从于亭利定律 的那个状态的化学势。：

该溶液就称为理想溶液或理想混合物，这就是理想溶液的热力学定义。 四、 理想溶液的通性 由理想溶液模型和热力学定义式子可以推出理想溶液具有以下通性： i. ∆mixV=0, 即由纯组分混合成溶液时，溶液的体积等于各组分的体积之和，而没有 额外的增加或减少。 ii. ∆mixH=0,这就是说在混合过程中，物质B的摩尔焓没有变化。所以混合前后总焓不 变，不产生热效应。 iii. 具有理想的混合熵。∆mix S= -R iv. 混合吉布斯自由能∆mixG。等温下，根据，∆G=∆H-∆S，应有∆mixG=∆mixH-∆mixS= RT， 由于<1，所以∆ mixG<0. v. 对于理想溶液，拉乌尔定律与亨利定律是没有区别的： = = §4.4 稀溶液中各组分的化学势 在理想稀溶液中，溶剂和溶质分别服从不同的规律，因此它们的化学势表示式具有不同 的具体内容，这是与理想溶液的不同之处。举二组分体系为例，A为溶剂，B为溶质。 1. 稀溶液的定义 两种挥发性物质组成一溶液，在一定的温度和压力下，在一定的浓度范围内，溶剂遵守 拉乌尔定律，溶质遵守亨利定律，这种溶液称为稀溶液。值得注意的是，化学热力学中的稀 溶液并不仅仅是指浓度很稀的溶液。 2. 溶剂的化学势 溶剂服从拉乌尔定律，其化学势应与理想溶液相同，即 = (T)+ RTln 3. 溶质的化学势 在溶液中对于溶质而言， = =(T)+ RTln 在稀溶液中溶质服从亨利定律， =。代入后得， = (T) +RTln（/ ） + RTln 或 ≈ (T)+ RTln （4-4-1） 其中 (T) 为标准态的化学势，可看作是在温度为T，压力 , 当=1，仍服从于亨利定律 的那个状态的化学势

R 溶质的标准态 P=kxAn 纯B 服从亨利定律 实际溶液 A←一XA XB→ B 图3-41溶液中溶质的标准态 (浓度为摩尔分数 这个状态可参阅图3-4-1，将=的直线延长所得到R点，这个由延伸而得到的状态实际上并不 存在。在图中纯B的状态由W点表示，这个假象的状态(R)是外推出来的，客观上并不存在， 因为不可能在从0一1的整个区间内，溶质都服从亨利定理。引入这样一个想象的标准态，并 不影响△G或4的计算，因为在求这些值时，有关标准态的项都消去了。P大，xX: 若将李利定维写腿中大是.号 的形式，则 4i≈Am①+RTnm 水公o:mn导 ☑①和H片（①也分别是以质最摩尔浓度和体积摩尔浓度表示组成时的标准态，可看作是 在温度为T,压力 =1mol.kgm,=1mol.dmC时仍服从亨利定律的那个状态的化学势。 显然，这些状态都是想象的。 §4.5稀溶液的依数性(colligative 早在18世纪就发，在发性剂中入非挥发性质贺能使器剂的气压降低， 点升高，冰点降低，并呈现渗透压力，稀溶液的这四种性质与所溶入的溶质的性质和数量无 关，而只取决于所含溶质粒子的数目，而与溶质的本性无关 们把这 性质称为依数性质 (oie properties)。溶质的粒子可以是分子、离子、大分子或胶粒。 一、蒸气压的降低 拉乌尔定律指出稀溶液中溶剂蒸气压与溶剂摩尔分数之间的关系为 PA= -A=PA XPPAX8 对于二组分稀溶液，加入非挥发性溶质B以后，溶剂的蒸气压会下降。这是造成凝固点 下降，沸点升高和渗透压的根本原因。 二、沸点(boiling point)上升 沸点是指液体的蒸气压等于外压时的温度。当液体的蒸气压等于标准压时的温度，便是

这个状态可参阅图3-4-1， 将 =的直线延长所得到R点，这个由延伸而得到的状态实际上并不 存在。在图中纯B的状态由W点表示，这个假象的状态（R）是外推出来的，客观上并不存在， 因为不可能在从0→1的整个区间内，溶质都服从亨利定理。引入这样一个想象的标准态，并 不影响∆G或∆µ的计算，因为在求这些值时，有关标准态的项都消去了。 若将亨利定律写成 = ，= 的形式，则 ≈ (T)+ RTln ≈ (T)+ RTln (T)和 (T)也分别是以质量摩尔浓度和体积摩尔浓度表示组成时的标准态，可看作是 在温度为T，压力 , =1mol.kg -1 , =1mol.dm -3 时仍服从亨利定律的那个状态的化学势。 显然，这些状态都是想象的。 §4.5 稀溶液的依数性（colligative properties） 早在18世纪就发现，在挥发性溶剂中加入非挥发性溶质，就能使溶剂的蒸气压降低，沸 点升高，冰点降低，并呈现渗透压力，稀溶液的这四种性质与所溶入的溶质的性质和数量无 关，而只取决于所含溶质粒子的数目，而与溶质的本性无关。我们把这种性质称为依数性质 (colligative properties)。溶质的粒子可以是分子、离子、大分子或胶粒。 一、 蒸气压的降低 拉乌尔定律指出稀溶液中溶剂蒸气压与溶剂摩尔分数之间的关系为 = -∆= 对于二组分稀溶液，加入非挥发性溶质B以后，溶剂A的蒸气压会下降。这是造成凝固点 下降，沸点升高和渗透压的根本原因。 二、 沸点（boiling point）上升 沸点是指液体的蒸气压等于外压时的温度。当液体的蒸气压等于标准压时的温度，便是

该液体的正常沸点。如图，3-5-1所示溶剂的蒸气压曲线为CC',在温度T”时，其蒸气压等于 标准压，故工为该纯溶剂的沸点。然而在纯溶剂中，一旦加入少量的非挥发性溶质，溶质的 燕气压较纯溶剂低△P。因而若要使溶液沸腾，其温度必须升高△T,至T',这是溶液的蒸气压才 等于标淮压的外压，即图中的D'点，△T就是溶液沸点的上升。可以从热力学函数得出沸点上 升与溶液浓度的定量关系。 D 溶剂 |△P C溶液 D/ △今T To' 图3-5-1液体的蒸气压曲线与沸点 若溶液浓度有d的变化，沸点相应地有dr的变化，可得x。 R(T)2 (4-5-1) R(T)2 K4,只国”女 (4-5-2) 称为沸点升高常数(boiling point elevation coefficients),单位是K.mol.kg,它只与溶剂的性 质有关。常用溶剂的K值有表可查。 例3-5-1苯的沸点为353.3弧，蒸发热为395J.g,试计算苯的摩尔沸点升高常数。 《4,H④， =8.314*(353.1)*78*10395*78)=2.63KKgm0l 、 冰点下降(freezing point) 固体溶剂与溶液成平衡时的温度称为溶液的凝固点。这里的凝固点指的是纯溶剂析出时 的温度。与沸点上升的数学处理完全相似，溶液冰点的下降随溶液浓度的关系为 △T=K,马 (4-5-3) R(T)2 真4A(西， (4-5-4) K,称为冰点下降常数(freezing point lowering coefficients),单位是K.mol.kg。其物 理意义为溶液浓度趋向于零的极限条件下，每1kg溶剂中溶入，的溶质而引起溶液冰点的下降 T,与溶液浓度m,的比值。常用溶剂的K值有表可查。 沸点上升与冰点下降的测定常用于确定溶质的相对分子质量 例3-5-212.2g苯甲酸C,HC00H溶于100g乙醇后，使乙醇沸点升高1.13K,若将12.2g

该液体的正常沸点。如图，3-5-1所示溶剂的蒸气压曲线为CC’，在温度Tb * 时，其蒸气压等于 标准压，故 Tb * 为该纯溶剂的沸点。然而在纯溶剂中，一旦加入少量的非挥发性溶质，溶质的 蒸气压较纯溶剂低∆P。因而若要使溶液沸腾，其温度必须升高∆Tb至Tb’,这是溶液的蒸气压才 等于标准压的外压，即图中的D’点，∆Tb就是溶液沸点的上升。可以从热力学函数得出沸点上 升与溶液浓度的定量关系。 若溶液浓度有d的变化，沸点相应地有dT的变化，可得 ∆Tb = = Kb mB (4— 5-1) Kb = （4-5-2） 称为沸点升高常数（boiling point elevation coefficients），单位是K.mol.-1 kg，它只与溶剂的性 质有关。常用溶剂的Kb值有表可查。 例3-5-1 苯的沸点为353.3K, 蒸发热为395J.g -1 ,试计算苯的摩尔沸点升高常数。 解：根据式（3-5-2） Kb= =8.314*(353.1) 2 *78*10 -3 /(395*78)=2.63K.Kg.mol -1 三、 冰点下降（freezing point） 固体溶剂与溶液成平衡时的温度称为溶液的凝固点。这里的凝固点指的是纯溶剂析出时 的温度。与沸点上升的数学处理完全相似，溶液冰点的下降随溶液浓度的关系为 ∆Tf = Kf mB (4-5-3) Kf = (4-5-4) Kf 称为冰点下降常数（freezing point lowering coefficients），单位是K.mol. -1 kg。其物 理意义为溶液浓度趋向于零的极限条件下，每1kg溶剂中溶入nB的溶质而引起溶液冰点的下降 ∆Tf与溶液浓度mB的比值。常用溶剂的Kf值有表可查。 沸点上升与冰点下降的测定常用于确定溶质的相对分子质量。 例3-5-2 12.2g苯甲酸C6H5COOH溶于100g乙醇后，使乙醇沸点升高1.13K,若将12.2g

苯甲酸溶于100g苯后，使苯的沸点生高1.36k,计算苯甲酸在两种溶剂中的分子量， 计算结果可说明什么问题？己知K:乙醇为1.23，苯为2.62。 解：根据稀溶液的沸点升高公式： w/M。 △T。=KA 在乙醇溶液中，MK*辄/(4T)=1.23*12.2/(1.13*100)=0.133kg.mo1 在苯中M2.62*12.2/(1.36*100)=0.235kg.mol 中程不程分学合果表明来甲酸在乙中基本上以单分 四、渗透压(osmotic pressure) 如图所示，在一个U型的容器内，用半透膜将纯溶剂和溶液分开，半透膜只允许溶剂分子 通过。设纯溶剂的化学势为？溶液中溶剂的化学势为4，。则 P+z 溶剂目溶液 半 诊 图3-5-2渗透k 因为山，<仙”，溶剂分子有自纯溶剂的一方进入溶液一方的倾向，为了阻止纯溶剂的一方的溶 剂分子进入溶液，需要在溶液上方施加额外的压力，以增加其蒸气压，使半透膜双方溶剂的 化学势相等而达到平衡，这个额外的压力就定义为渗透压，用Π表示。若令D和即，分别代表平 衡时溶剂和溶液上的外压，则 右：4：=度=以()+n 4 (T)RTLnP p+RTLnx =M (T,P)+RTLnX. II p -p. (4-5-5) 根据渗透平衡可得： ,R”R-”R=CR 这就是渗透压公式，也枝称为范特霍夫公式(van't Hoff公式)。C是溶质的浓度，浓度不能 五、依数性的关联 溶液的浓度与△T,、△T

苯甲酸溶于100g苯后，使苯的沸点生高1.36k,计算苯甲酸在两种溶剂中的分子量， 计算结果可说明什么问题？已知Kb：乙醇为1.23，苯为2.62。 解：根据稀溶液的沸点升高公式： ∆Tb== mB= Kb 在乙醇溶液中，MB = Kb *WB /(∆Tb WA )= 1.23*12.2/(1.13*100)=0.133kg.mol-1 在苯中MB =2.62*12.2/(1.36*100)=0.235 kg.mol-1 由原子量计算苯甲酸的分子量为0.122 kg.mol -1 ，实验结果表明苯甲酸在乙醇中基本上以单分 子形式存在，而在苯中基本上以二聚分子缔合形式存在。 四、 渗透压（osmotic pressure） 如图所示，在一个U型的容器内，用半透膜将纯溶剂和溶液分开，半透膜只允许溶剂分子 通过。设纯溶剂的化学势为µA，溶液中溶剂的化学势为µA ’。则 因为µA ’ <µA ∗ ，溶剂分子有自纯溶剂的一方进入溶液一方的倾向，为了阻止纯溶剂的一方的溶 剂分子进入溶液，需要在溶液上方施加额外的压力，以增加其蒸气压，使半透膜双方溶剂的 化学势相等而达到平衡，这个额外的压力就定义为渗透压，用Π表示。若令p和p2分别代表平 衡时溶剂和溶液上的外压，则 Π = p - p2 （4-5-5） 根据渗透平衡可得： 这就是渗透压公式，也被称为范特霍夫公式（van’t Hoff公式）。C B 是溶质的浓度，浓度不能 五、 依数性的关联 溶液的浓度与∆Tb 、∆Tf