《基础化学》课程授课教案（物理化学讲义）第九章 化学动力学

第九章化学动力学 一、教学方案 ①掌据瞬时反应速率的表示方法及基元反应、反应级数、速率常数等基本 今 ②明确反应级数与反应分子数的区别： ③掌据具有简单级数的反应（如零级、一级、二级）的动力学速率方程的 特征，并能由实验数据确定简单反应级数。对三级反应只作一般了解： ④对典型的的三种复合反应（对峙反应、平行反应、连串反应）要掌握其 各自的特点： 包费物的多响，男用A经癸公式的物宽意义.计院 ⑥掌握链反应的特点，会应用稳态近似、平衡假使等近似处理方法。 ①反应级数的确定： 2.教学重点 ②简单级数的反应的特征 ③温度对反应速率的影响。 3.教学难点 的商定 4数学方别 ①授课全部用多媒体电子教案，告别了传统的粉笔加黑板的单一教学模式： ②辅导答疑采用电子邮件及在线论坛等模式： 和手段 ③测验、考试的试卷由试题库自动组卷及试题分析。 ①§7-1化学反应速率及其测定(1学时) §7-2反应物浓度对反应速率的影响(2学时) 5教内 7应数的学 1学时) 分配 一7快速反应的研究方法1学时 ⑧§77温度对反应速率的影响(2学时) 二、教案内容 91反应速率及其测定 一化学动力学的任务及其研究内穷 1化学动力学与化学热力学的联系与区别 研究任何一个化学反应，往往要注意两个重要方面： (1)化学反应的方向和限度问题。在指定条件（体系及其相关的环境）下，在给 物 可，反应是否能 发生？如能发生，进行到

第九章 化学动力学 一、教学方案 1. 教学目的 和要求 ① 掌握瞬时反应速率的表示方法及基元反应、反应级数、速率常数等基本 概念： ② 明确反应级数与反应分子数的区别； ③ 掌握具有简单级数的反应（如零级、一级、二级）的动力学速率方程的 特征，并能由实验数据确定简单反应级数。对三级反应只作一般了解； ④ 对典型的的三种复合反应（对峙反应、平行反应、连串反应）要掌握其 各自的特点； ⑤ 掌握温度对反应速率的影响，明确Arrhenius经验公式的物理意义，计算 E a 、A、k等物理量； ⑥ 掌握链反应的特点，会应用稳态近似、平衡假使等近似处理方法。 2. 教学重点 ① 反应级数的确定； ② 简单级数的反应的特征； ③ 温度对反应速率的影响。 3. 教学难点 ① 反应级数的确定; ② 链反应。 4. 教学方法 和手段 ① 授课全部用多媒体电子教案，告别了传统的粉笔加黑板的单一教学模式； ② 辅导答疑采用电子邮件及在线论坛等模式; ③ 测验、考试的试卷由试题库自动组卷及试题分析。 5. 教学内容 及 课 时 分配 ① §7-1化学反应速率及其测定(1学时) ② §7-2反应物浓度对反应速率的影响(2学时) ③ §7-3 反应基数的确定(1学时) ④ §7-4基元反应、反应分子数(1学时) ⑤ §7-5 对峙反应、平行反应、连串反应 (2学时) ⑥ §7-6链反应(1学时) ⑦ §7-7快速反应的研究方法(1学时) ⑧ §7-7温度对反应速率的影响（2学时） 二、教案内容 9-1 反应速率及其测定 一. 化学动力学的任务及其研究内容 1 化学动力学与化学热力学的联系与区别 研究任何一个化学反应，往往要注意两个重要方面： （1） 化学反应的方向和限度问题。在指定条件（体系及其相关的环境）下，在给 定的始态（反应物）和终态（产物）之间，反应是否能够发生？如能发生，进行到 什么程度为止？这类问题的研究，是靠化学热力学来解决的

(2)化学反应的速率和机理问题。要弄清楚化学反应体系从始态到终态所经历过 程的细节，发生这个过程所需要的时间，以及影响这种过程的因素等等。这类问题 是靠化学动力学来解决的。化学动力学(Chemical kineties)是研究化学反应速率及 反应机理的科学，它和化学热力学既有联系又有区别。 个化学反应，必须通过热力 学的计算，判 务件空生反应的提下再来进行化 在 zy] 子的研究， 安 例如在298 能机理， 应提供理论依 H,(g)+专0.(g)=H00.AG°=-237.2Kmo1 实际上 据热力学的计算，这一反应发生的趋势限大，但却不能表明反应以多大速率进行 相 实现反应的条件 句题。例如上述反应，如果把温度升高到70OK,它便以犀炸的方式快速进行。 2化学动力学的任务及其研究内容 化学动力学的主要任务时研究反应速率及其所遵循的规律和各种因素对反应速率的影 响，从而给人们提供化学反应的条件，揭示化学反应历程，找出决定反应谏率的关静所在， 使反应按照我们所需要的方向进行，并得到人们所希望的产品。它包括以下三个层次的研究 内容：1)宏观反应动力学。它是以宏观反应动力学实验为基础的，研究从复合反应到基元 反应的动力学行为，由于这方面的研究在化 生产中起着十分重要的作用，所以它在理论和 上获 基元反应动力学、它 队天重的威观 字 技不 外化学冷光 借于量子力学 化学动学较之花学热学来说是学行新兴的学科，其理论和实验技术 都存在若一系列的疑难问题有待解决。 二反应速率(reaction rate) 的各种物质的物质 地变化，所以反应速度 般指的是瞬时速度 产物) 、反物 图91-1反应物、产物的浓度c随时间t的关系时高压一级反应Alg2k=Ak 对一个按确定计量式进行的反应 0 传统定义：反应速率定义为：单位时间，单位体积，某种物质因反应而增加或减少的物质的 量

（2） 化学反应的速率和机理问题。要弄清楚化学反应体系从始态到终态所经历过 程的细节，发生这个过程所需要的时间，以及影响这种过程的因素等等。这类问题 是靠化学动力学来解决的。化学动力学（Chemical kinetics）是研究化学反应速率及 反应机理的科学，它和化学热力学既有联系又有区别。一个化学反应,必须通过热力 学的计算,判定在给定条件、可以发生反应的前提下再来进行化学动力学的研究，否 则将是徒劳的。化学动力学主要是研究化学反应的速率，研究各种外在因素对反应 速率的影响；研究物质的结构、性质与反应性能的关系，探讨能够解释这种反应速 率规律的可能机理，为最优化控制反应提供理论依据。 例如在298K时 H 2 (g) + O 2 (g) = H 2 O (l), ∆G Θ m =-237.2KJ·mol -1 根据热力学的计算，这一反应发生的趋势很大，但却不能表明反应以多大速率进行。 实际上，在一般温度下，此反应几乎不会发生。要想解决在什么条件下才能实现反应的问题， 必需进行动力学研究。只有通过这类研究，找到实现反应的条件以后，才能全面地解决实际 问题。例如上述反应，如果把温度升高到700K，它便以爆炸的方式快速进行。 2 化学动力学的任务及其研究内容 化学动力学的主要任务时研究反应速率及其所遵循的规律和各种因素对反应速率的影 响，从而给人们提供化学反应的条件，揭示化学反应历程，找出决定反应速率的关键所在， 使反应按照我们所需要的方向进行，并得到人们所希望的产品。它包括以下三个层次的研究 内容：1）宏观反应动力学。它是以宏观反应动力学实验为基础的，研究从复合反应到基元 反应的动力学行为，由于这方面的研究在化工生产中起着十分重要的作用，所以它在理论和 应用的研究上获得了很大的发展；2）基元反应动力学。它是以大量的微观分子反应动力学 行为为出发点，借助于统计力学的方法，研究宏观反应动力学行为；3）分子反应动力学。 这是近年来新发展的一个领域，它通过分子束散射技术和远红外化学冷光，凭借于量子力学 的理论模型，研究单个分子通过碰撞发生变化的动力学行为。 从历史上看，化学动力学较之化学热力学来说是一门新兴的学科，其理论和实验技术， 都存在着一系列的疑难问题有待解决。 二.反应速率 (reaction rate) 一反应从开始到达平衡前，反应物逐渐减少，产物逐渐增加（见图9-1-1），参加反应 的各种物质的物质量随时间在不断地变化，所以反应速度一般指的是瞬时速度。 图9-1-1反应物、产物的浓度c随时间t的关系 时高压一级反应AB0lg2kzzAIk= 对一个按确定计量式进行的反应 0=∑ B 传统定义：反应速率定义为:单位时间,单位体积,某种物质因反应而增加或减少的物质的 量

品 对于恒容反应 例如： N+3H,→2NH 可以用 中参加反应的物质来量度反应速率。但因反应计量系数的限制，选用不同物 质来量度反应速率时，其数值不 正相同 它们乙 可的关系是 用不物质造成反应速率不一致的缺陷，国际理论与应用化学协会规定 比率来表示反应速度 定义：=- (91-1) d5= (91-2) 19.1-31 任意时刻，参加反应的各种物质所起反应的摩尔数与它们各自的计最系数之比是一个常数 3 一常数只随反应时间而变化与物质种类无关。因此，可以用反应进度随时间的变化率来量 度反应速度。 该定义与传统定义区别在于反应速度不受所选物质不同而改变，原定义称为反应物消耗速率 压力比浓度容量测定因此也可用参加反应各物种的分压米代替浓度例如对 鲁学. r-RTr 对子 相化 称会定条件下的比活性，Q为催化剂的量， 表示催化剂的量可以用质量m表示，也可以用堆体积V表示，也可用表面积A表示。 三反应速率的测定(determination of reaction rate) 从原则上看，只要测定不同时刻反应物或产物的浓度，便可以求出反应速率，测定方法 一般有化学法和物理法。 1化学 化学反应的某 时刻取出部分样品后，必须使反应停止不再继续进行 并尽可能快封 测窖琴铆能浓度。停止的方法有骤冷、冲稀、加阻化剂或移走化剂等，然后用化学方法 关键. 取出样品立即冻结 优点：能直接得到不同时刻的绝对值，所用仪器简单

r=± 对于恒容反应 r=± 例如: N 2 + 3H 2 → 2NH 3 r=- r=- r= 可以用任一种参加反应的物质来量度反应速率。但因反应计量系数的限制，选用不同物 质来量度反应速率时,其数值不一定相同。它们之间的关系是 - =- = 为了克服因选用不同物质而造成反应速率不一致的缺陷，国际理论与应用化学协会规定 用反应进度对时间的变化率来表示反应速度。 定义：r= = (9-1-1) = d = r= 对于恒容体系：r= (9-1-2) aA +bB =dD +eE r=- =- = = (9-1-3) 任意时刻,参加反应的各种物质所起反应的摩尔数与它们各自的计量系数之比是一个常数， 这一常数只随反应时间而变化与物质种类无关。因此，可以用反应进度随时间的变化率来量 度反应速度。 该定义与传统定义区别在于反应速度不受所选物质不同而改变，原定义称为反应物消耗速率 或产物的生成速率。 对于气相反应,压力比浓度容量测定,因此也可用参加反应各物种的分压来代替浓度,例如对 N 2 + 3H 2 → 2NH 3 r ' =- = - = r=- =- = r ' =RTr (7-1-4) 对于多相催化反应 r= (7-1-5) 称给定条件下的比活性，Q为催化剂的量。 表示催化剂的量,可以用质量m表示,也可以用堆体积V表示,也可用表面积A表示。 三 反应速率的测定(determination of reaction rate) 从原则上看，只要测定不同时刻反应物或产物的浓度，便可以求出反应速率，测定方法 一般有化学法和物理法。 1.化学法 在化学反应的某一时刻取出部分样品后，必须使反应停止不再继续进行，并尽可能快地 测定某物质的浓度，停止的方法有骤冷、冲稀、加阻化剂或移走催化剂等，然后用化学方法 进行分析测定。 关键：取出样品立即冻结 优点：能直接得到不同时刻的绝对值，所用仪器简单

缺点：分析操作繁杂。 2物有-长物蛋性顶与浓度底单植面数的关系，测定反应体系物理隆时间的安化，经后 壁故的冰德麻型型歌物“防金靠热整竹务是 测的是整个反应体系的物理量，而我们一般需要的是某一时刻某种反应物或产物的浓度，所 以用物理方法测定反应速度首先要找出体系的物理量与某种物质浓度的关系。 一般用无表示体系的某种物理量(P,V,L4)等，人▣元，九分别表示0，问=时 刻体系的物理性质，C0C表示t=0,气，时刻某种物质的浓度，它们之间有下列关系 C。x(.) C(心.)且比例系数相同。 例乙酸乙酯皂化反应 CH COOC,H,+NaOH C→，H,OH+CH,COONa 随反应进行，由于离子电导很高的OH转化为离子电导较低的CH3COO-,因此整个反应 体系的电导将降低，我们可以利用电导仪测量出反应体系的初始电导L。不同时刻的电导 以及反应终了时的电导L,体系电导的变化与反应程度成正比“ 92反应物浓度对反应速率的影响 速幸方程式和速率常数 1.反应速率方程式(reaction rate equation) 影响反应速率的因素很多：浓度，温度，催化剂等等。其中最重要的是浓度对反应速率 的影响，表示反应速率和浓度的关系式叫做反应速率方程式，也叫动力学方程式。 ”=(C,有微分式和积分式两种形式。有了速率方程式，就可以清楚的看出浓度是如 何影响反应速度的，在化工生产中可以作为设计反应器的重要依据。也是确定反应机理的主 零依据。研究动力学首先要建立动力学方程式，是否任写一个反应式就能写出它的动力学方 例： H+C,2 HCI r=kCC-,a, H,+Br,2HBr =kCC→游”味 H+H→2H=kCC 个反应，计量系数相同，但动力 子万程4 同。说明它们机理不同，速率方程是由实验 测出来的。根据实验数据，归纳整理成速率方 2速率常数(rat nt) 速率方程中 数称速率常数 意义：各反应物的浓度等于1时的反应速常，其值大小与浓度无关，而与反应温度，反应木

缺点：分析操作繁杂。 2.物理法 利用一些物理性质与浓度成单值函数的关系，测定反应体系物理量随时间的变化，然后 折算成不同时刻反应物的浓度值，通常可利用的物理量有P,V,L, .A等。这种方法优点是 迅速方便，不终止反应。可在反应器内连续监测，便于自动记录。所要注意的是：这种方法 测的是整个反应体系的物理量,而我们一般需要的是某一时刻某种反应物或产物的浓度，所 以用物理方法测定反应速度,首先要找出体系的物理量与某种物质浓度的关系。 一般用 表示体系的某种物理量（P,V,L, ）等， t 分别表示t=0, t=t, t= 时 刻体系的物理性质，C 0 ,C t 表示t=0, t=t,时刻某种物质的浓度,它们之间有下列关系 C 0 ( - ) C t ∝ ( - t ) 且比例系数相同。 = 例乙酸乙酯皂化反应 CH 3 COOC 2 H 5 + NaOH C 2 H 5 OH + CH 3 COONa 随反应进行,由于离子电导很高的OH-转化为离子电导较低的CH3COO-，因此整个反应 体系的电导将降低，我们可以利用电导仪测量出反应体系的初始电导L 0 ,不同时刻的电导Lt 以及反应终了时的电导L,体系电导的变化与反应程度成正比 = 9-2 反应物浓度对反应速率的影响 一. 速率方程式和速率常数 1. 反应速率方程式（reaction rate equation） 影响反应速率的因素很多：浓度，温度，催化剂等等。其中最重要的是浓度对反应速率 的影响，表示反应速率和浓度的关系式叫做反应速率方程式，也叫动力学方程式， ，有微分式和积分式两种形式。有了速率方程式，就可以清楚的看出浓度是如 何影响反应速度的，在化工生产中可以作为设计反应器的重要依据。也是确定反应机理的主 要依据。研究动力学首先要建立动力学方程式，是否任写一个反应式就能写出它的动力学方 程式呢? 例： H 2 + Cl 2 2HCl r=kCC H 2 + Br 2 2HBr r= k C·C /1+k / H 2 +I 2 2HI r= kCC 三个反应，计量系数相同，但动力学方程不同。说明它们机理不同，速率方程是由实验 测出来的。根据实验数据，归纳整理成速率方程。 2.速率常数（rate constant） 速率方程中的比例系数称速率常数。 意义：各反应物的浓度等于1时的反应速率，其值大小与浓度无关，而与反应温度，反应本

性，催化剂，溶剂等因素有关。对于一定反应，在一定条件下是个常数。 音发的的买系具有浓度华柔积的形式 =kC”·C。.(92-1) 分别质的分级。+是整个反安的数 例如H+L 对H,和L,分别为一级，对反应来说该反应为二级。 ()反应级数a 均由实验确定：其数值可以随反应条件改变，可以是简单的级数反应 度速率无 对于不能写成浓度幂乘积形式的速率方程，叫级数无意义。 以上介绍的是动力学方程的微分形式，即速率方程，它只能告诉我们反应速度随组分 的浓度变化的情况并不能直接告诉我们们浓度随反应时间的变化情况。实际应用中，人们往 往想知道经过多长时间，浓度变为多少，或者达到一定的转化率需要多少时间。为了方便地 得到浓度C和函数关系，需要对微分式进行积分，得到动力学方程的积分形式。以下根据反 应级数的动力学分类来讨论。 三一级反应(first order reaction) 级反应 蜕变，某此化合物的分裂，分子重排等等 若某一级反应的计量式为：AP一 其速率方程的微分方程.金=kC(9-2-2) 移项积分 」光=kdt 可得lnC=kt+B(9-2-3) 当=O时，C-C得B=lnC。 n=kt k-h子 (9-24) C-Ce (9-25) 其中C是反应物在t时刻的浓度，C,是反应物的初始浓度。以上各式均称动力学的积分式。 销质然个版度有的流皮七 k=}n品 (92-6) 若令y代表时刻，原始反应己分解的百分数，即转化率 y k=n (9.2.7 令y支，原始反应物已分解了50%，即反应物消耗一半，此时，所需时间。量c

性，催化剂，溶剂等因素有关。对于一定反应，在一定条件下是个常数。 二. 反应级数（order of reaction） 当一反应的速率与反应物浓度的关系具有浓度幂乘积的形式 r= kC A α ·C B β . (9-2-1) α,β.分别是物质A，B.的分级数， n=α+β+.，是整个反应的级数。 例如H 2 + I 2 2HI r= kCC 对H 2和I 2分别为一级，对反应来说该反应为二级。 (1) 反应级数α，β.均由实验确定，其数值可以随反应条件改变,可以是简单的级数反应 0，1，2，3级，也可以是分数级反应或负数级反应。 (2) 反应级数是反应物浓度对反应速率影响的方次数，表示各物质浓度对反应速率的影响程 度，级数越高，则该物质的变化对反应速度的影响越重要，零级反应说明浓度的改变对 反应速率无影响。 对于不能写成浓度幂乘积形式的速率方程，叫级数无意义。 以上介绍的是动力学方程的微分形式，即速率方程，它只能告诉我们反应速度随组分 的浓度变化的情况,并不能直接告诉我们浓度随反应时间的变化情况。实际应用中，人们往 往想知道经过多长时间，浓度变为多少,或者达到一定的转化率需要多少时间。为了方便地 得到浓度C和t函数关系，需要对微分式进行积分，得到动力学方程的积分形式。以下根据反 应级数的动力学分类来讨论。 三 一级反应（first order reaction） 反应速率与反应物浓度的一次方成正比的反应称为一级反应。 一级反应例子很多，放射性元素的蜕变，某此化合物的分裂，分子重排等等。 若某一级反应的计量式为：AP 其速率方程的微分方程- =k 1 C (9-2-2) 移项积分 -∫ = k 1 dt 可得lnC=-k 1 t + B (9-2-3) 当t=0时，C=C 0 得B=lnC 0 ln = k 1 t k 1 = ln (9-2-4) C=C 0 e - (9-2-5) 其中C是反应物在t时刻的浓度，C 0是反应物的初始浓度。以上各式均称动力学的积分式。 动力学方程形式根据解题方便可以有不同形式： 若令x代表t时刻,反应物反应掉的浓度，则此时反应物的浓度C=C 0 -x k 1 = ln (9-2-6) 若令y代表t时刻，原始反应已分解的百分数，即转化率 y = k 1 = Ln (9-2-7) 令y= ，原始反应物已分解了50%，即反应物消耗一半，此时，所需时间t 称为半衰期（half life）

要 一级反应半衰期与反应速率常数成反比，与反应物初始浓度无关，给定反应，是个常数。 反应物消耗34所需时间：寻=n云 一级反应的分数寿期均与反应物初始浓度无关，给定反应下是一个常数。 讨论一级反应的特点 1.lC对t作图是一直线，其斜率等于速率常数的负值（见图9-2-1）。 图9-21一级反应的nc图 2k的单位是[时间，S,min,h 1反应当反应浓度降为始浓度的1%时需时若将反应物起始浓度提高二 加快反应速度，当反应物浓度降为起始浓度1%时，需时5，则 【>【 t=【 【<【 1414 例2：C可存在于有生命的树木中，C放射性蚁变的：6665730年，测得一个考古样里仍含 有生命树木72%C”的木质，问考古样距今有多少年？ 解：K=K=子n 四.二级反应(Second order reaction 凡是 的浓度的平方（减两种物质浓度的乘积）成正比的反应称为二级 如酯化，硝化等反应都是二级反应。 当cc时，k(9-2-10) 若总反应式为 A+B即与 0 a-X 以产物的生成速率表示反应速率，则

t = = (9-2-8) 一级反应半衰期与反应速率常数成反比，与反应物初始浓度无关，给定反应，是个常数。 反应物消耗3/4所需时间t = Ln 一级反应的分数寿期均与反应物初始浓度无关，给定反应下是一个常数。 讨论一级反应的特点 1.lnC对t作图是一直线，其斜率等于速率常数的负值(见图9-2-1)。 图9-2-1一级反应的ln-c图 2.k 1的单位是[时间] -1 ，S -1 , min -1 ,h -1 。 3.t 与初始浓度无关,仅与K 1 成反比, 一定反应为常数,其它分数寿期也一样。同一反应,不管初始浓度为多少，只要达到相同的转化率，则所需要的时间都是一样的。 例１：某一级反应,当反应浓度降为起始浓度的1%时,需时t 1 s若将反应物起始浓度提高一倍, 加快反应速度,当反应物浓度降为起始浓度1%时,需时t 2 s, 则 t 1 > t 2 t 1 = t 2 t 1 < t 2 某化学反应其反应消耗3/4所需时间使它消耗1/2所需时间的2倍，则反应为 0 1 2 3 级 一级反应的一种重要的用途就是测定矿石年龄和考古样品的年代 例２：C可存在于有生命的树木中, C放射性蜕变的t 1/2 =5730年，测得一个考古样里仍含 有生命树木72% C 14 的木质，问考古样距今有多少年? 解：K 1 = K 1 = Ln K 1 = = =1.209×10 -4 年 －１ T= = =2714年 四.二级反应（Second order reaction） 凡是反应速率与反应物的浓度的平方(或两种物质浓度的乘积)成正比的反应称为二级 反应。二级反应较普遍，大部分有机反应，如酯化,硝化等反应都是二级反应。 二级反应速率方程式为：r=k 2 c A c B (9-2-9) 当c A =c B 时，r=k 2 c 2 (9-2-10) 若总反应式为 A +BP t=0 a b 0 t a-x b-x x 以产物P的生成速率表示反应速率，则有

r音-kaxb-9(9-2山 设A和B的起始浓度相等，即ab,则上式化为 面=k(ax) 移项积分 a奇=k,h 六-是=k (9-2-12) aix)=kl k=a-可(9-2.13) 若令y代表t时刻，原始反应物已分解的分数 v=d k=ia(9-2.14) 当Y=12时，即原始反应物消耗一半时， (=a (9-2-15) 级反应的半衰期与起始浓度成反比。对于相同的转化率，如果初始浓度减半，时间 1,以立对作图应得一直线，直线的斜率等于速率常数k,k的单位通常为 dm·mol·s 2.二级反应的半衰期与起始浓度成反比。这可作为判断二级反应的依据。 当ab时，其速率方程式为 鲁kexb 移项得 a-c-可=k,dl 积分 at-西=k,dl 左边：会【六h=6 =六血÷-ln).六h8别 故郁÷血哥 (9-2-16) 以血号对作图可得一直线，由其斜率可求得速率常数，的值。K的单位为mm0g 对这种情况，不提半衰期。 五三级反应(third order reaction) 凡是应速 与反应物浓度的三次方（或三种浓度的乘积）成正比的反应，称为三级 反应。三级反应可有下列三种类型. 1)3AP> 2)2A+B-→P 3)A+B+CP→

r= =k 2 (a-x)(b-x) (9-2-11) 设A和B的起始浓度相等，即a=b，则上式化为 ＝k 2 (a-x) 2 移项积分 (9-2-12) 或 k 2 = (9-2-13) 若令y代表t时刻,原始反应物已分解的分数 y= k 2 = (9-2-14) 当Y=1/2时，即原始反应物消耗一半时， (9-2-15) 二级反应的半衰期与起始浓度成反比。对于相同的转化率，如果初始浓度减半，时间 加倍，这是二级反应的特征。 讨论： １.以 对t作图应得一直线 ，直线的斜率等于速率常数k 2 ，k 2 的单位通常为 dm 3 ·mol -1 ·s -1 。 2. 二级反应的半衰期与起始浓度成反比。这可作为判断二级反应的依据。 当ab时，其速率方程式为 =k 2 (a-x)(b-x) 移项得 积分 左边= = = = 故有k 2 t= (9-2-16) 或k 2 t= + (9-2-17) 以 对t作图可得一直线，由其斜率可求得速率常数k 2 的值。K 2 的单位为dm 3 ·mol -1 ·s -1 。 对这种情况，不提半衰期。 五.三级反应(third order reaction) 凡是反应速率与反应物浓度的三次方（或三种浓度的乘积）成正比的反应，称为三级 反应。三级反应可有下列三种类型． １）３AP ２）2A+B→ P ３）A+B+CP

仅讨论最简单的一种情况，即第三种类型。 A+B CP 0 a-x b-x c-x x 速率方程为 鲁=k（axb-xe-9(92-18) 当a=b-c时，上式化为 鲁=ka29-219 k=女中)9-220 k的量纲为[浓度]2.[时间] 其半衰期 三级反应较少见尤其在气相反应中更少见现已知的仅有5个这些反应都与NO有关 2NO+H. NO+HO 2NO+O NO. 2NO+CI 2NOCI 2NO+Br, 2NOBr 2NO+D. N20+D,0 ction 动力学速率方程为=.帝大(92-21) 移项积分得：c=k,+B 当t=0时c=c 故c=k+6。(9222) 当c=2时，可得半衰期与起始浓度成正比 t 季级反应的 征 字袋的半期与初始物浓度成正比，与反应速率常数，成反比：以c对作图得一直 线，其斜率即为k 例如NH在W丝上分解，一些皂化反应和异相催化反应。对于某一个参加反应的物质而言， 表9-2-1简单反应的速率方程及半衰期 级反应式 起始浓度条件 速率公式 积分式 半衰 数 期 零A→产物 CA.0=a -=k cA=a-kpl 级 A→产物 CA.0=Q -=kCA Inca=Ina-kt

仅讨论最简单的一种情况，即第三种类型。 A+ B+ CP t=0 a b c 0 t a-x b-x c-x x 速率方程为 ＝k 3 (a-x)(b-x)(c-x) (9-2-18) 当a=b=c时，上式化为 ＝k 3 (a-x) 3 (9-2-19) 移项积分得 = k 3 = ) (9-2-20) k 3 的量纲为［浓度］ －２ ·［时间］ －１ 其半衰期t ＝ 三级反应较少见,尤其在气相反应中更少见,现已知的仅有5个,这些反应都与NO有关. 2NO + H 2 N 2 O + H 2 O 2NO + O 2 NO 2 2NO + Cl 2 2NOCl 2NO + Br 2 2NOBr 2NO + D 2 N2O + D 2 O 六. 零级反应（zero order reaction） 反应速率与参加反应的物质浓度无关时称为零级反应。 动力学速率方程为r=- =k 0 (9-2-21) 移项积分得：c=-k 0 t+B 当t=0时c=c 0 故c=-k 0 t+ c 0 (9-2-22) 当c= 时，可得半衰期与起始浓度成正比 t ＝ (7-2-23) 零级反应的特征： 零级反应的半衰期与初始物浓度成正比，与反应速率常数k 0成反比；以c对t作图得一直 线，其斜率即为-k 0。 例如NH 3在W丝上分解，一些皂化反应和异相催化反应。对于某一个参加反应的物质而言， 级数是零的反应是常见的。 以上讨论了几种具有简单级数的反应的速率方程式，现将有关公式列于表7-2-1。 表9-2-1简单反应的速率方程及半衰期 级 数 反应式 起始浓度条件 速率公式 积分式 半衰 期 零 级 一 级

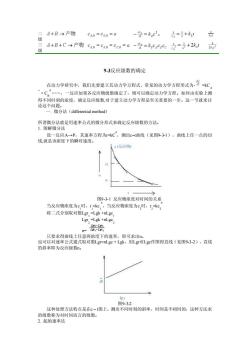
A+B→产物CA0=Ca.0=Q -号=k,c24=+k10 级 +B+C→产物C%n=C0=Ce0=a-号=k04c9e之=+2kg 93反应级数的确定 在动力学研究中，我们先要建立其动力学方程式，常见的动力学方程形式为.等C ”·C.,一反应如果各反应物级数确定了，则可以确定动力学方程。如何由实验上测 得不同时刻的浓度，确定反应级数，对于建立动力学方程是至关重要的一步。这一节就来讨 论这个问题。 一.微分法(differential method) 设一反应A一→P,其速率方程为kC”,测出c曲线（见图93-1），曲线上任一点的切 线，就是该浓度下的瞬时速度。 图931反应物浓度对时间的关系 当反应物浓度为c时，=kc,，当反应物浓度为c,时，【，k。 将二式分别取对数Lgr,=Lgk+nlgc Lgr,=Lgk+nLgc 授 ,即可求出n Lgc作图得直线（见图9-3-2），直线 的斜率 为反应级数n。 图9-3-2 这种处理方法特点是在©-t图上，测出不同时刻的斜率，时间是不相同的，这种方法求 的级数称为对时间而言的级数。 2.起始速率法

二 级 三 级 9-3反应级数的确定 在动力学研究中，我们先要建立其动力学方程式，常见的动力学方程形式为- =kC A α ·C B β .，一反应如果各反应物级数确定了，则可以确定动力学方程。如何由实验上测 得不同时刻的浓度，确定反应级数,对于建立动力学方程是至关重要的一步。这一节就来讨 论这个问题。 一. 微分法（differential method） 所谓微分法就是用速率公式的微分形式来确定反应级数的方法。 1. 图解微分法 设一反应A→ P，其速率方程为r=kC n ，测出c–t曲线（见图9-3-1），曲线上任一点的切 线,就是该浓度下的瞬时速度。 图9-3-1 反应物浓度对时间的关系 当反应物浓度为c 1 时，r 1 =kc 1 n ，当反应物浓度为c 2 时，r 2 =kc 2 n 将二式分别取对数Lgr 1 =Lgk +nLgc 1 Lgr 2 =Lgk +nLgc 2 n= 只要求得曲线上任意两浓度下的速率，即可求出n。 也可以对速率公式通式取对数Lgr=nLgc + Lgk，用Lgr对Lgc作图得直线（见图9-3-2），直线 的斜率即为反应级数n。 图9-3-2 这种处理方法特点是在c –t图上，测出不同时刻的斜率，时间是不相同的，这种方法求 的级数称为对时间而言的级数。 2. 起始速率法

从不同的起始浓度开始，测量开始一段时间的浓度变化，在不同的起始浓度测量不同 的起始速度，相当于图933中各曲线在O时的斜率。然后Lg对Lgc作图，得一直线，由 斜率可求出n。Lgr=Lgk+nLg9 数较为可靠 ]为起始速率不受产物和其他因素的影响，相当于无干扰因 图933 对简单级数，两种处理方法结果一致。 对复杂级数，两种处理方法结果不大一致。 若有两种或两种以上物质参与反应，且各反应物质起始浓度不相等，其速率方程为： 仍可采用微分法，分别求得级数a、B.实验中，先将B. 物质大大付量，或 在各次试验中使用相同浓度的其他物质，而只变A物质的起始浓度，得到不同起始浓度的 解时速率。k4。 Lg=Lg“+BLgg求出B, 整个反应级数为na+B+ thod 0级：1品 1级：支之 2级：t这 3级：动 t之=A阳 =() Lgg)

从不同的起始浓度开始，测量开始一段时间的浓度变化，在不同的起始浓度测量不同 的起始速度，相当于图9-3-3中各曲线在t=0时的斜率。然后以Lgr 0 对Lgc作图，得一直线，由 斜率可求出n。Lgr 0 =Lgk +nLgc 0 这种方法求得的级数较为可靠，因为起始速率不受产物和其他因素的影响，相当于无干扰因 素的级数，称为对浓度而言的级数。 图9-3-3 对简单级数,两种处理方法结果一致。 对复杂级数,两种处理方法结果不大一致。 若有两种或两种以上物质参与反应，且各反应物质起始浓度不相等，其速率方程为： r=kc A α·c B β. 仍可采用微分法，分别求得级数α、β.，实验中，先将B. . .等物质大大过量，或 在各次试验中使用相同浓度的其他物质，而只改变A物质的起始浓度，得到不同起始浓度的 瞬时速率。r=k / cα ，这里k / =kc B β ，Lgr= Lgk / +αLg c,求出α。然后将除B以外的物质大大过量,或保持不变，只改变B物质的起始浓度，得到不同起始浓度的速率。r // =k // c B Lgr / = Lgk // +βLg c B，求出β。 整个反应级数为n= α+β+. 二.半衰期法（half life method） 不同的级数反应,其半衰期与反应起始浓度的关系为 0级：t ＝ 1级：t = 2级：t = 3级：t ＝ t =Aa 1-n 以两个不同起始浓度a和a / 进行实验 对同一反应A相同 =（ ） n-1 Lg =Lg（ ） n-1