《基础化学》课程授课教案（分析化学讲义）第二章 误差及分析数据的统计处理

第二章误差及分析数据的统计处理 定量分析的任务是准确测定组分在试样中的含最。在测定过程中 即使采 用最可靠的分析方法，使用最精密的仪器，由技术很熟练的人员进行操作，也不 可能得到绝对准确的结果。因为在任何测量过程中，误差是客观存在的。因此 我们应该了解分析过程中误差产生的原因及其出现的规律，以便采取相应措施 减少误差。另一方面需要对测试数据进行正确的统计处理，以获得最可靠的数 §2一1定量分析中的误差 误差与准确度 误差(cror)是指测定值x与真值μ之差。误差的大小可用绝对误差E (absolute error)和相对误差Er(relative error)表示，即 E=x:一4 E,=-严×100% 相对误差表示误差占真值的百分率。 例如分析天平称量两物体的质量各为1.6380g和0.1637g,假定两者的 真实质量分别为1.6381g和0.1638g,则两者称量的绝对误差分别为 E,=二080×10%=-0.06 E,=0.1638×100%=-0.06% 两者称量的相对误差分别为 E=1.6380-1.6381=-0.0001 E=0.1637-0.1638=-0.0001 由此可知，绝对误差相等，相对误差并不一定相同，上例中第一个称量结果 的相对误差为第二个称量结果相对误差的十分之一。也就是说，同样的绝对误 差，当被测定的量较大时，相对误差就比较小，测定的准确度也就比较高。因 此，用相对误差来表示各种情况下测定结果的准确度更为确切些

第二章 误差及分析数据的统计处理 定量分析的任务是准确测定组分在试样中的含量。在测定过程中，即使采 用最可靠的分析方法，使用最精密的仪器，由技术很熟练的人员进行操作，也不 可能得到绝对准确的结果。因为在任何测量过程中，误差是客观存在的。因此 我们应该了解分析过程中误差产生的原因及其出现的规律，以便采取相应措施 减少误差。另一方面需要对测试数据进行正确的统计处理，以获得最可靠的数 §2－1 定量分析中的误差 误差与准确度 误差(error)是指测定值 xi 与真值μ之差。误差的大小可用绝对误差 E (absolute error)和相对误差 Er (relative error)表示，即 相对误差表示误差占真值的百分率。 例如分析天平称量两物体的质量各为 1．638 0g 和 0．163 7g，假定两者的 真实质量分别为 1．638 1g 和 0．163 8 g，则两者称量的绝对误差分别为 两者称量的相对误差分别为 由此可知，绝对误差相等，相对误差并不一定相同，上例中第一个称量结果 的相对误差为第二个称量结果相对误差的十分之一。也就是说，同样的绝对误 差，当被测定的量较大时，相对误差就比较小，测定的准确度也就比较高。因 此，用相对误差来表示各种情况下测定结果的准确度更为确切些

绝对误差和相对误差都有正值和负值。正值表示分析结果偏高，负值表示 分析结果偏低， 实际工作中，真值实际上是无法获得的，人们常常用纯物质的理论值、国家 标准局提供的标准参考物质的证书上给出的数值或多次测定结果的平均值当 作真值。 准确度(a )是指测定平均值与真值接近的程度，常用误差大小表示 误差小，准确度高 偏差与精密度 偏差(deviation)是指个别测定结果x与几次测定结果的平均值王之间的 差别。与误差相似， 偏差也有绝对偏差d和相对偏差4之分： 测定结果与平 均值之差为绝对偏差，绝对偏差在平均值中所占的百分率或千分率为相对偏 差 d =x-i (2-3) d,=5,×100% (2-4) 各偏差值的绝对值的平均值，称为单次测定的平均偏差，又称算术平均 偏差(average deviation),既 a=空d=空-到 (2-5) 单次测定的相对平均偏差表示为 a,=是×100% (2-6) 标准偏羌(standarddeviation)又称均方根偏差，当测定次数趋于无限多 称为总体标准偏差，用表示如下： 2(x- G=1 (2-7) 式中μ为总体平均值，在校正了系统误差情况下，μ即代表真值，为测定次数 在一般的分析工作中，测定次数是有限的，这时的标准偏差称为样本标 准差以s表示： 式中（一1）表示n个测定值中具有独立偏差的数目，又称为自由度。 常用下式计算标准偏差更为方便：

绝对误差和相对误差都有正值和负值。正值表示分析结果偏高，负值表示 分析结果偏低。 实际工作中，真值实际上是无法获得的，人们常常用纯物质的理论值、国家 标准局提供的标准参考物质的证书上给出的数值或多次测定结果的平均值当 作真值。 准确度(accuracy)是指测定平均值与真值接近的程度，常用误差大小表示。 误差小，准确度高。 偏差与精密度 偏差(deviation)是指个别测定结果 xi 与几次测定结果的平均值王之间的 差别。与误差相似，偏差也有绝对偏差 di 和相对偏差 dr之分。测定结果与平 均值之差为绝对偏差，绝对偏差在平均值中所占的百分率或千分率为相对偏 差。 各偏差值的绝对值的平均值，称为单次测定的平均偏差 d~，又称算术平均 偏差（average deviation）,既 单次测定的相对平均偏差 d~表示为 标准偏差(standarddeviation)又称均方根偏差，当测定次数趋于无限多 称为总体标准偏差，用σ表示如下： 式中μ为总体平均值，在校正了系统误差情况下，μ即代表真值，n 为测定次数。 在一般的分析工作中，测定次数是有限的，这时的标准偏差称为样本标 准差以 s 表示： 式中(n—1)表示 n 个测定值中具有独立偏差的数目，又称为自由度。 常用下式计算标准偏差更为方便：

s= n-1 (2-9) s与平均值之比称为相对标准偏差，以s表示，也可简写为SD: 5,= (2-10) s.如以百分率表示又称为变异系数CV(coef田Iclent of variation。 精密度(precision)是指在确定条件下，将测试方法实施多次，求出所得结果 之间的一致程度。精密度的大小常用偏差表示。 精密度的高低还常用重复性 tabilhy)和再现性(rep 重复性)：同一操作者，在相同条件下，获得 一系列结果之间的一致程度 再现性®)：不同的操作者，在不同条件下，用相同方法获得的单个结果之 间的一致程度。 在偏差的表示中，用标准偏差更合理，因为将单次测定值的偏差平方后 将较大的偏差显著地表现出来。 例1有两组测定值 ☒ 判断精密度的差异。 解：平均值r甲=3.0平均偏差d甲=0.08标准偏若5甲=0.08 22=3.0 dz=0.08 -0.14 本例中，两组数据的平均偏差是一样的。但数据的离散程度不一致，乙组数 据更分散，说明用平均偏差有时不能反映出客观情况， 而用标准偏差来判断，本 例中5乙大一些，即精密度差一些，反映了真实情况。因此在一般情况下，对测 定数据应表示出标准偏差或变异系数。 准确度与精密度的关系 确度与精密度的关系，如图2一1所示 如图2一1表示甲、己、丙丁四人测定同一试 真值37.40% 样中铁含量时所得的结果。由图可见：甲所得 结果准确度和精密度均好，已的结果精密度星 的精密度很差，虽然平均值接近真 但带有偶然性，是大的正负误差抵消的结果 其结果也的不可靠的。由此可知，试验结果首 先要求精密度高，才能保证有准确的结果， 36.00%36.50%37.00%37.50%38.00% 图2-1不同工作者分析同一试样的结果 (表示个别测定 表示平均值)

s 与平均值之比称为相对标准偏差，以 sr表示，也可简写为 RSD： sr如以百分率表示又称为变异系数 CV(coefflclent of variation)。 精密度(precision)是指在确定条件下，将测试方法实施多次，求出所得结果 之间的一致程度。精密度的大小常用偏差表示。 精密度的高低还常用重复性(repeatabilhy)和再现性(reproduciblity)表示。 重复性(r)：同一操作者，在相同条件下，获得一系列结果之间的一致程度。 再现性(R)：不同的操作者，在不同条件下，用相同方法获得的单个结果之 间的一致程度。 在偏差的表示中，用标准偏差更合理，因为将单次测定值的偏差平方后 将较大的偏差显著地表现出来。 例1 有两组测定值 ' 判断精密度的差异。 本例中，两组数据的平均偏差是一样的，但数据的离散程度不一致，乙组数 据更分散，说明用平均偏差有时不能反映出客观情况，而用标准偏差来判断，本 例中 s 乙 大一些，即精密度差一些，反映了真实情况。因此在一般情况下，对测 定数据应表示出标准偏差或变异系数。 准确度与精密度的关系 准确度与精密度的关系，如图 2—1所示。 如图 2—1 表示甲、已、丙丁四人测定同一试 样中铁含量时所得的结果。由图可见：甲所得 结果准确度和精密度均好，已的结果精密度虽 然好，但准确度稍差；丙的精密度和准确度都 很差；丁的精密度很差，虽然平均值接近真值， 但带有偶然性，是大的正负误差抵消的结果， 其结果也的不可靠的。由此可知，试验结果首 先要求精密度高，才能保证有准确的结果

但高的精密度也不一定能保证有高的准确度（如无系统误差存在，则精密度高，准确度也高。 倒2分析铁矿中铁含量，得如下数据：37.45%，37.20%，37.50%，37.30%，37.25%。 计算此结果的平均值，平均偏差，标准偏差，变异系数。 37.45%+37.20%+37.50%+37.30%+37.25% -37.34% 各次测量偏差分别是 d1=+0.11%d2=-0.14%d=+0.16%d=-0.04%dy=-0.09% -(0.11+0.14+0.16+0.04+0.09)%=0.1% =会-√@+00g9+040.01B CV=5=73×100%-0.35%

但高的精密度也不一定能保证有高的准确度(如无系统误差存在，则精密度高，准确度也高)

误差的分类及减鱼误差的方法 根据误差产生的原因及其性质的不同分为两类 系统误差或称可测误差 (determlnateerror),随机误差(randomerror)域称偶然误差。 1,系统误差 产生的原因 )方法不完善造成的方法误差(methoderor) 的影响：滴定分析中指示剂选择不当 (2)试剂或蔡馏 纯度不够， 带人微最的待测组分，干扰测定等原因造成 (3)测量仪器木身缺陷造成的仪器误差((instrumentalerror),如容量器皿刻 度不准又未经校正，电子仪器“噪声”过大等造成。 (4操作人员操作不当或操作偏见浩成的人为误差(D onalerror.如观 察颜色偏深或偏浅，第二次读数总是想与第一次重复等造席 其中方法误差有时不被人们察觉，带来的影响 较大 应特别注意。 系统误差的性质： ()重复性：同一条件下，重复测定中，重复地出现。 2)单向性：测定结果系统偏高或偏低。 3)误差大小基本不变，对测定结果的影响比较恒定 以测定出来，对测定结果进行校正。 校正系统误差的方法：针对系统误差产生的原因，可采用选择标准方法、进 行试剂的提纯和使用校正值等办法加以消除。如选择一种标准方法与所采用 的方法作对照试验或选择与试样组成接近的标准试样作对照试验，找出校正值 加以校正。对试剂或实验用水是否带人被测成分，或所含杂质是否有干扰，可 通过空白试验扣 空白值加以校正 空白试验是指除了不加试样外，其他试验步骤与试样试验步骤完全 实验，所得结果称为空白值。 是否存在系统误差，常常通过回收试验加以检查。 回收试验是在测定试样某组分含量(x)的基础上，加入已知量的该组分 (®，再次测定其组分含量(x》。由回收试验所得数据可以计算出回收率。 回收率=4×100% 由回收率的高低来判断有无系统误差存在。对常量组分回收率要求商 般为99%以 对微量组分回收率要求在90%一110%。 2.随机误差 随机误差是由一些无法控制的不确定因素所引起的，如环境温度、湿度、电 压、污染情况等的变化引起试样质量、组成、仪器性能等的微小变化，操作人员 实验过程中操作上的微小差别，以及其他不确定因素等所造成的误差。这类误 差值时大时小， 时正时负 难以找到具体 原 更无法 测量它的值。但从多次 测量结果的误差米看，仍然符合一定的规律，实际工作中，随机误差与系统误差 并无明显的界限，当人们对误差产生的原因尚未认识时，往往把它当作偶然误 差对待，进行统计处理

误差的分类及减免误差的方法 根据误差产生的原因及其性质的不同分为两类①：系统误差或称可测误差 (determlnateerror)，随机误差(randomerror)或称偶然误差。 1．系统误差 产生的原因 (1)方法不完善造成的方法误差(methoderror) 的影响；滴定分析中指示剂选择不当。 (2)试剂或蒸馏水纯度不够，带人微量的待测组分，干扰测定等原因造成。 (3)测量仪器本身缺陷造成的仪器误差(instrumentalerror)，如容量器皿刻 度不准又未经校正，电子仪器“噪声”过大等造成。 (4)操作人员操作不当或操作偏见造成的人为误差(personalerror)，如观 察颜色偏深或偏浅，第二次读数总是想与第一次重复等造席 其中方法误差有时不被人们察觉，带来的影响也较大。 应特别注意。 系统误差的性质： (1)重复性：同一条件下，重复测定中，重复地出现。 (2)单向性：测定结果系统偏高或偏低。 (3)误差大小基本不变，对测定结果的影响比较恒定。 以测定出来，对测定结果进行校正。 校正系统误差的方法：针对系统误差产生的原因，可采用选择标准方法、进 行试剂的提纯和使用校正值等办法加以消除。如选择一种标准方法与所采用 的方法作对照试验或选择与试样组成接近的标准试样作对照试验，找出校正值 加以校正。对试剂或实验用水是否带人被测成分，或所含杂质是否有干扰，可 通过空白试验扣除空白值加以校正。 空白试验是指除了不加试样外，其他试验步骤与试样试验步骤完全 实验，所得结果称为空白值。 是否存在系统误差，常常通过回收试验加以检查。 回收试验是在测定试样某组分含量(x1)的基础上，加入已知量的该组分 (x2)，再次测定其组分含量(x3)。由回收试验所得数据可以计算出回收率。 由回收率的高低来判断有无系统误差存在。对常量组分回收率要求高 般为 99％以上，对微量组分回收率要求在 90％～110％。 2．随机误差 随机误差是由一些无法控制的不确定因素所引起的，如环境温度、湿度、电 压、污染情况等的变化引起试样质量、组成、仪器性能等的微小变化，操作人员 实验过程中操作上的微小差别，以及其他不确定因素等所造成的误差。这类误 差值时大时小，时正时负，难以找到具体的原因，更无法测量它的值。但从多次 测量结果的误差来看，仍然符合一定的规律，实际工作中，随机误差与系统误差 并无明显的界限，当人们对误差产生的原因尚未认识时，往往把它当作偶然误 差对待，进行统计处理

随机误差的分布服从正态分布 如测定次数较多，在系统误差已经排除的情况下，随机误差的分布也有一 定的规律，如以横坐标表示随机误差的值，纵坐标表示误差出现的概率大小，当 测定次数无限多时，划得随机误差正态分布曲线，见图2一2。 上1 图2-2标准正态分布曲线 定义 (2-11) 随机误差分布具有以下性质： (1)对称性：大小相近的正误差和负误差出现的概率相等，误差分布曲线是 对称的。 (2)单峰性：小误差出现的概率大，大误差出现的概率小，很大误差出现的 概率非常小。误差分布曲线只有一个峰值。误差有明显的集中趋势。 (3)有界性：仅仅由于偶然误差造成的误差不可能很大，即大误差出现的概 率很小。如果发现误差很大的测定值出现，往往是由于其他过失误差造成 时，对这种数据应作相应的处理。 (4)抵偿性：误差的算术平均值的极限为零 (2-12) 在标准正态分布曲线上，如把曲线与横华标从O至+O之间所句相的面 积代表所有随机误差出现的概率的总和)定为100%，通过计算发现误差范围 与出现的概率有如下关系（见表2一1和图2一2）。 表2-1误差在某些区间出现的概率 Y-" [=g,+8] 【-1,1] 68.3% [-1.96a,+1.960] [-1.96,+1.96 95% -2a,+2c “2+ [-3a,+3 3.+3 99.7%

随机误差的分布服从正态分布 如测定次数较多，在系统误差已经排除的情况下，随机误差的分布也有一 定的规律，如以横坐标表示随机误差的值，纵坐标表示误差出现的概率大小，当 测定次数无限多时，则得随机误差正态分布曲线，见图 2—2。 随机误差分布具有以下性质： (1)对称性：大小相近的正误差和负误差出现的概率相等，误差分布曲线是 对称的。 (2)单峰性：小误差出现的概率大，大误差出现的概率小，很大误差出现的 概率非常小。误差分布曲线只有一个峰值。误差有明显的集中趋势。 (3)有界性：仅仅由于偶然误差造成的误差不可能很大，即大误差出现的概 率很小。如果发现误差很大的测定值出现，往往是由于其他过失误差造成 时，对这种数据应作相应的处理。 (4)抵偿性：误差的算术平均值的极限为零。 在标准正态分布曲线上，如把曲线与横坐标从—O 至+O 之间所包围的面 积(代表所有随机误差出现的概率的总和)定为 100％，通过计算发现误差范围 与出现的概率有如下关系(见表 2—1 和图 2—2)

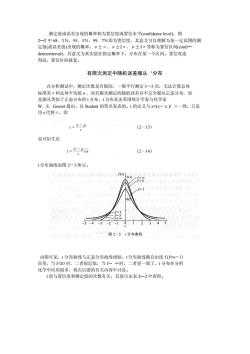
测定值或误差出现的概率称为置信度或置信水平(confidence level),图 2一2中68.3%，95.5%，99.7%即为置信度，其意义可以理解为某一定范围的测 定值（或误差值）出现的概率。 +2 3o等称为置信区间(confi denceinterval),其意义为真实值在指定概率下，分布在某一个区间。置信度选 得高，置信区间就宽。 有限次测定中随机误差服从‘分布 在分析测试中，测定次数是有限的，一般平行测定3~5次 无法计算总体 标准差σ和总体平均值，而有限次测定的随机误差并不完全服从正态分布，而 是服从类似于正态分布的t分布，t分布是由英国统计学家与化学家 骨，代。提，以的笔名发表，：的定又与一V。-我风足 t=1 (2-13) 也可衍生出 t=所 (2-14) 分布曲线如图2一3所示。 八) 0.4 (a5 图2-3t分布曲线 而变，当20时， 二者很近似，当f一∞时， 化学中应用很多，将在后面的有关内容中讨论。 【值与置信度和测定值的次数有关，其值可由表2一2中查得

测定值或误差出现的概率称为置信度或置信水平(confidence level)，图 2—2 中 68．3％，95．5％，99．7％即为置信度，其意义可以理解为某一定范围的测 定值(或误差值)出现的概率。μ±σ、μ±2σ、μ±3σ等称为置信区间(confi— denceinterval)，其意义为真实值在指定概率下，分布在某一个区间。置信度选 得高，置信区间就宽。 有限次测定中随机误差服从‘分布 在分析测试中，测定次数是有限的，一般平行测定 3～5 次，无法计算总体 标准差σ和总体平均值μ，而有限次测定的随机误差并不完全服从正态分布，而 是服从类似于正态分布的 t 分布，t 分布是由英国统计学家与化学家 W．S．Gosset 提出，以 Student 的笔名发表的。t 的定义与 x=(x－μ)/ σ一致，只是 用 s 代替σ，即 也可衍生出 t 分布曲线如图 2－3所示。 由图可见，t 分布曲线与正态分布曲线相似，t 分布曲线随自由度 f (f=n－1) 而变，当 f>20 时，二者很近似，当 f→ ∞时，二者更一致了，t 分布在分析 化学中应用很多，将在后面的有关内容中讨论。 t 值与置信度和测定值的次数有关，其值可由表 2—2中查得

表2-21值表 置信度 测定次数 90% 95% 999% 6.314 12.706 63.657 2.920 4.30 9.925 2.353 3.182 5.841 5 2.132 2.776 4.60 2.015 2.57 678901 250 1.812 2.228 3.169 1725 2.08 2846 1.645 1.960 2.576 由t的定义式(2.14)可衍生得 回 置信区间的宽窄与置信度、测定值的精密度和测定次数有关，当测定值精 密度愈高s值愈小)，测定次数愈多们值愈大)时，置信区间愈窄，即平均值愈 接近真值，平均值念可靠。 式(2一15)的意义：在一定置信度下（如95%），真值（总体平均值）将在测定 平均值x附近的一个区间即在至 之间存在，把握程度为95%。 式(2一15)常作为分析结果的表达式。 置信度选择越高，置信区间越宽，其区间包括真值的可能性也就越大，在分析 化学中，一般将置信度定为95%或90%。 例3测定S02的质量分数，得到下列数据(%)：28.62,28.59,28.51,28.48,28.52. 28.63。求平均值，标准偏差及置信度分别为90%和95%时平均值的置信区间。 解： 王-(28.62+28.59+28.51+28.48+28.52+28.63)%=28.56% =√006+000±0.050.8+0.0+0.02%=0.06 查表2-2，置信度为90%，n=6时，1=2.015，因此 -(86±20500）%=(086±05 同理，对于置信度为95%，可得 -(28.6±25g00）%=(28.56±0.07)% 上述计算说明，若平均值的置信区间取(28.56士0.05)%，则真值在其中出 现的概率为90%，而若使真值出现的概率提高为95%，则其平均值的置信区间 将扩大为(28.56±0.07%

由 t 的定义式（2 - 14）可衍生得 置信区间的宽窄与置信度、测定值的精密度和测定次数有关，当测定值精 密度愈高(s 值愈小)，测定次数愈多(n 值愈大)时，置信区间愈窄，即平均值愈 接近真值，平均值愈可靠。 式(2—15)的意义：在一定置信度下(如 95％)，真值(总体平均值)将在测定 平均值 x 附近的一个区间即在 至 之间存在，把握程度为 95％。 式(2—15)常作为分析结果的表达式。 置信度选择越高，置信区间越宽，其区间包括真值的可能性也就越大，在分析 化学中，一般将置信度定为 95%或 90%。 上述计算说明，若平均值的置信区间取(28．56±0．05)％，则真值在其中出 现的概率为 90％，而若使真值出现的概率提高为 95％，则其平均值的置信区间 将扩大为(28．56±0．07)％

例4测定钢中含铬量时，先测定两次，测得的质量分数为1,12%和1.15%：再测定三 次.测得的数据为1.11%，1.16%和1.12%。试分别按两次测定和按五次测定的数据来计 算平均值的置信区间(95%置信度)。 解：两次测定时 =1.12%+1.15%=1.135% -√o0产001%-0.01% 查表2-2，得%=12.7(n=2,因此 o-1.14±2.1x002)%=1.14±0.19% 五次测定时 =1.2+15+11+L.16+1.2%=1.13% 查表2-2，得95%=2.78(n=5),因此 o-5:2g）水-a5o8 由上例可见，在一定测定次数范围内，适当增加测定次数，可使置信区间显 苦缩小，即可使测定的平均值×与总体平均μ接近 公 差 “公差”是生产部门对于分析结果允许误差的一种表示方法。如果分析结 果超出允许的公差范围，称为“超差”，该项分析工作应该重做。 公差的确定与很多因素有关，一般是根据试样的组成和分析方法的准确度 来确定。对组成较复杂（如天然矿石）的分析，允许公差范围贫 般工业 分析，允许相对误差在百分之几到千分之几，而原子量的测定，要求相对误差很 小。对于每一项具体的分析工作，有关主管部门都规定了具体的公差范围，例 如对钢中的硫含量分析的允许公差范围如下： 硫的质量分数/%≤0.0200.020-0.0500.050-0.1000.100-0.200≥0.200 公差（绝对误差）/%土0.002±0.04±0.006±0.010±0.015 目前，国家标准中，对含量与允许公差之关系常常用回归方程式表示

五次测定时 由上例可见，在一定测定次数范围内，适当增加测定次数，可使置信区间显 著缩小，即可使测定的平均值 x 与总体平均μ接近。 公 差 “公差”是生产部门对于分析结果允许误差的一种表示方法。如果分析结 果超出允许的公差范围，称为“超差”，该项分析工作应该重做。 公差的确定与很多因素有关，一般是根据试样的组成和分析方法的准确度 来确定。对组成较复杂(如天然矿石)的分析，允许公差范围宽一些，一般工业 分析，允许相对误差在百分之几到千分之几，而原子量的测定，要求相对误差很 小。对于每一项具体的分析工作，有关主管部门都规定了具体的公差范围，例 如对钢中的硫含量分析的允许公差范围如下： 目前，国家标准中，对含量与允许公差之关系常常用回归方程式表示

§2一2分析结果的数据处理 分析工作者获得了一系列数据后，需对这些数据进行处理，譬如有个别偏 离较大的数据（称为离群值或极值）是保留还是该弃去测得的平均值与真值 不能随意 舍去。 可疑数据的取舍 数据中出现个别值离群太远时，首先要仔细检查测定过程中，是否有操作 错误，是否有过失误差（粗差）存在，不能随意地舍弃离群值以提高精密度，而是 需进行统计处理。即判断离群值是否仍在偶然误差范围内，常用的统计检验方 法有Grubbs检验法和Q值检验法(Q-test),这些方法都是建立在随机误差服 从一定的分布规律基础上。 步骤是：将测定值由小到大排列，XG(置信度选95%)，则x1或 。应弃去，反之则保留。G表见表2一3

§2—2 分析结果的数据处理 分析工作者获得了一系列数据后，需对这些数据进行处理，譬如有个别偏 离较大的数据(称为离群值或极值)是保留还是该弃去?测得的平均值与真值 或标准值的差异是否合理，相同方法测得的两组数据或用两种不同方法对同一 试样测得的两组数据间的差异是否在允许的范围内，都应作出判断，不能随意 舍去。 可疑数据的取舍 数据中出现个别值离群太远时，首先要仔细检查测定过程中，是否有操作 错误，是否有过失误差(粗差)存在，不能随意地舍弃离群值以提高精密度，而是 需进行统计处理。即判断离群值是否仍在偶然误差范围内，常用的统计检验方 法有 Grubbs 检验法和 Q 值检验法(Q—test)，这些方法都是建立在随机误差服 从一定的分布规律基础上。 1．Grubbs 法 步骤是：将测定值由小到大排列，x1＜x2＜.＜xn其中 x1或 xn可疑，需 要进行判断，算出 n 个测定值的平均值 x 及标准偏差 s。 需要判断 x1按 计算； 需要判断 xn,，按 计算 得出的 G 计算值若大于表中临界值，G 计算>G 表(置信度选 95％)，则 x1 或 xn 应弃去，反之则保留。G 表见表 2—3