《高等数学》课程教学资源（作业习题）D9 多元函数微分法及其应用

第九章多元函数撒分法及其应用班级： 姓名： 序号： 9-1多元函数的基本概念 一、填空、选择题 1.函数：=ln(y2-2x+1)的定义域为 2.函数：=x-√的定义域为 3.函数u=acco6F+ 一的定义域为 4.函数=4-x2-y2-2+ r+少严+：的定义线为 1-y= 5.iowx产+y 69” 7.设函数f(x,y)= r+m4+y0,则，列在点00-（ 1 0 x2+y2=0 (A)无定义 (B)不存在极限(C)极限为0(D)不连续 8.设函数fx,) r+y +*0,则x》在点(0,0) 0. x2+y2=0 (A)无定义 (B)不存在极限 (C)极限为0(D)连续 二、计算下列极限 2-√y+4 1.h o xy 2 yuny

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 1 9-1 多元函数的基本概念 一、填空、选择题 1. 函数 ln( 2 1) 2 z  y  x  的定义域为 . 2. 函数 z  x  y 的定义域为 . 3. 函数 2 2 arccos x y z u   的定义域为 . 4. 函数 1 1 4 2 2 2 2 2 2         x y z u x y z 的定义域为 . 5. 2 2 ( , ) (0,1 1 lim x y xy x y    ） = . 6. y xy x y sin lim ( , )(3,0） = . 7. 设函数             0, 0 , 0 1 ( )sin ( , ) 2 2 2 2 2 2 2 2 x y x y x y x y f x y ，则 f (x, y) 在点(0,0) （ ） （A）无定义 （B）不存在极限 （C）极限为 0 （D）不连续 8.设函数            0 0 0 ( , ) 2 2 2 2 2 2 x y x y x y xy f x y ， ， ，则 f (x, y) 在点(0,0) （ ） （A）无定义 （B）不存在极限 （C）极限为 0 （D）连续 二、计算下列极限 1. xy xy x y 2 4 lim ( , ) (0,0    ） 2. x y xy x y tan lim ( , )(0,2）

1-c0s(x2+y2) 3.e 三、写出二元函数：=√1-x2-y2的定义域并描绘函数的图形 因、证明一不作在 五、证明w=0 2

2 3. 2 2 ( ) 1 cos( ) lim 2 2 2 2 ( , ) (0,0 x y x y x y e x y     ） 三、写出二元函数 2 2 z  1 x  y 的定义域并描绘函数的图形. 四、证明 x y x y x y   ( , )(0,0） lim 不存在. 五、证明 lim 0 ( , ) (0,0 2 2    x y xy x y ）

第九章多元函数撒分法及其应用班级： 姓名： 序号： 9-2偏导数与全微分 一、填空、选择题 1.设：=ln(x+y2),则全微分d止 2.设f(x,y,)=y2+z2+x2,则f(1,0,2)= 3曲线=+ 4一在点(2,4,5)处的切线对于x轴的倾角为 (y=4 [sinxy 4.设fx,y)={y2 y0,则f.0,)= 0,y=0, 6.=f(x,)在P(x)处∫.(x,)、∫，(，)存在是函数在该点可微分的.（） (A)必要条件： (B)充分条件： (C)充要条件： (D)既非必要亦非充分条件 二、求下列函数的偏导数 1.=sin xy+cos xy 2.:=(1+xyy 3.u-xi

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 3 9-2 偏导数与全微分 一、填空、选择题 1. 设 ln( ) 2 z  x  y ，则全微分dz  . 2. 设 2 2 2 f (x, y, z)  xy  yz  zx ，则 f xz (1,0,2)  . 3. 曲线         4 4 2 2 y x y z 在点(2,4,5)处的切线对于 x 轴的倾角为 . 4. 设         0, 0, , 0, sin ( , ) 2 xy xy y xy f x y 则 f x (0,1)  . 5. 设 x y z  x sin ，则       y z y x z x . 6. z  f (x, y)在 ( , ) 0 0 0 P x y 处 f (x, y) x 、 f (x, y) y 存在是函数在该点可微分的 （ ） （A）必要条件； （B）充分条件； （C）充要条件； （D）既非必要亦非充分条件. 二、求下列函数的偏导数 1. z xy xy 2  sin  cos 2. y z  (1 xy) 3. zy u  x

三设：的，求证会y房2 瓜®酸m子密等 五、求下列函数的全徽分 2、u=x

4 三、设 ) 1 1 ( x y z e    ，求证： z y z y x z x 2 2 2       . 四、设函数 x y z  arctan ，求 , 2 2 2 2 2 x y z y z x z        ， . 五、求下列函数的全微分 1、 y x z  xy  2、 yz u  x

第九章多元画数搬分法及其应用班级： 姓名： 序号： 9-3多元复合函数的求导法则、隐函数的求导公式 1硬=，商n小，则尝 2设：=aca.而)y=c, .dz 3使，商-亭汉-2，来察等 4.求下列函数的一阶偏导数（其中∫具有一阶连续偏导数） (1)z=fx2-y2,e) (2)=f(x,y,y2) 5设一心+方，种/精=阶号数来器 6便：心宁，其中了具有龄猪这9收器高器

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 5 9-3 多元复合函数的求导法则、隐函数的求导公式 1. 设 x y z e 2  ，而 3 x  sin t, y  t ，则  t z d d . 2. 设 z  arctan(xy)，而 x y  e ，则  x z d d . 3. 设 z u ln v 2  ，而 v x y y x u  ,  3  2 ，求 , y z x z     . 4.求下列函数的一阶偏导数（其中 f 具有一阶连续偏导数） （1） ( , ) 2 2 xy z  f x  y e （2）u  f (x, xy, xyz) 5.设 z  f (x 2  y 2），其中 f 具有二阶导数，求 , 2 2 2 x y z x z      . 6.设 ( , ) y x z  f x ，其中 f 具有二阶连续偏导数，求 2 2 2 2 2 , , y z x y z x z       

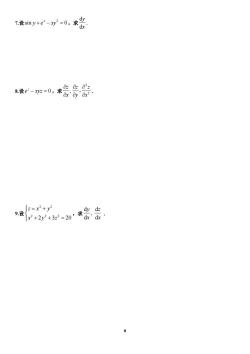
7设+-w=0,密 设=0，会等器 2-20出告 ,2=x2+y2

6 7.设sin 0 2 y  e  xy  x ，求 x y d d . 8.设e  xyz  0 z ，求 2 2 , x z y z x z       ， . 9.设          2 3 20 2 2 2 2 2 x y z z x y ，求 d d , d d x z x y

第九章多元函数撒分法及其应用班级： 姓名： 序号： 9-4多元函数微分学的几何应用 一、填空题 1、曲线x=t,y=t2,z=t上点 的切线平行于平面x+2y+z=4 2、曲线，少=4红 在点(L,2,)处的切线方程为 2=2-x 3、曲面e-:+y=3在点(21,0)处的切平面为 法线为 4、椭球面x2+2y2+3z2=6在点(1，-1,1)处的法线方程是 求曲线x=一y=中，2三1在对应于1=1点处的切线及法平面方程 x2+y2+2-3x=0 三、求曲线2x-3)+5:-4=0在点1,1D处的切线及法平面方程

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 7 9-4 多元函数微分学的几何应用 一、填空题 1、曲线 2 3 x  t, y  t ,z  t 上点 的切线平行于平面 x  2y  z  4 . 2、曲线        z x y x 2 4 2 2 在点(1, 2,1) 处的切线方程为 . 3、曲面e  z  xy  3 z 在点(2 ,1, 0) 处的切平面为 ， 法线为 . 4、椭球面 2 2 2 x  2y  3z  6 在点(1,1,1) 处的法线方程是 . 二、求曲线 2 , 1 , 1 z t t t y t t x      在对应于t 1点处的切线及法平面方程. 三、求曲线            2 3 5 4 0 3 0 2 2 2 x y z x y z x 在点(1,1,1) 处的切线及法平面方程

四、求椭球面x2+2y2+z2=1上平行于平面x-y+2z=0的切平面方程， 五、试证曲面√F+√少+√E=√a(a>0)任何点处的切平面在各坐标轴上的截距之和等于a

8 四、求椭球面 2 1 2 2 2 x  y  z  上平行于平面 x  y  2z  0 的切平面方程. 五、试证曲面 x  y  z  a (a  0) 任何点处的切平面在各坐标轴上的截距之和等于 a

第九章多元函数撒分法及其应用班级： 姓名： 序号： 9-5方向导数与梯度 一、填空题 1、函数：-ln(x+3y)在点(2，)处沿向量i-i+j方向的方向导数为 2、函数：=2x2+y2在点(1，-1)的梯度为 3、设f(x,y,)=ln(x2+y2+z2),则gradf0,2,-2)= 4、函数：=x2-2y+y2在点(2,3)处方向导数的最大值为 三、求函数=矿+一0在点L2)处沿方向角为a-号月-营7-号的方向的方向导数 3 三、求函数M=y+2+x知在点P(2,-1,2)处沿点P向径方向的方向导数

第九章 多元函数微分法及其应用 班级： 姓名： 序号： 9 9-5 方向导数与梯度 一、填空题 1、函数 z  ln(x  3y)在点(2,1) 处沿向量l i j      方向的方向导数为 . 2、函数 2 2 z  2x  y 在点(1, 1)的梯度为 . 3、设 ( , , ) ln( ) 2 2 2 f x y z  x  y  z ，则grad f (1, 2,  2)  . 4、函数 2 2 z  x  2xy  y 在点(2, 3)处方向导数的最大值为 . 二、求函数 u  xy  z  xyz 2 3 在点(1,1, 2) 处沿方向角为 3 , 4 , 3          的方向的方向导数. 三、求函数 u  xy  yz  xz 在点 P(2, 1, 2) 处沿点 P 向径方向的方向导数

四、求函数：=x2+y2在点ML,2)处沿从M。到M,(2,2+√5)的方向的方向导数. 五、求函数u=y2:在点M①，-L,2)处，从M。指向M,(2,L-)方向的方向导数，并求函数在M。点 处的最大方向导数 六、设球面x2+y2+z2=14在点P1,3,2)处的外法线方向为元，求函数u=x+y2+:在点P沿方向 n的方向导数

10 四、求函数 2 2 z  x  y 在点 (1, 2) M0 处沿从M 0到 (2, 2 3) M1  的方向的方向导数. 五、求函数u xy z 2  在点 (1, 1,2) M 0  处，从M 0指向 (2,1, 1) M1  方向的方向导数，并求函数在M 0点 处的最大方向导数. 六、设球面 14 2 2 2 x  y  z  在点 (1, 3, 2) P0 处的外法线方向为n  ，求函数 2 3 u  x  y  z 在点 P0沿方向 n  的方向导数