《误差理论及测量平差基础》课程教学资源（授课教案）教案24

?成金娜内素古科技大学INNERMONGOLIAUNIVERSITYOFSCIENCE&TECHNOLOGY教案课程名称测量平差基础总学时数80学时使用班级测绘专 2013-1、2任课学期2014/2015学年第一学期任课教师燕志明编制时间2014年11月24日

教 案 课程名称 测量平差基础 总学时数 80 学 时 使用班级 测绘专 2013-1、2 任课学期 2014/2015 学年第一学期 任课教师 燕志明 编制时间 2014 年 11 月 24 日

内蒙古科技大学教案课程名称：测量平差基础第二章条件平差授课章节83.5导线网条件方程式掌握导线网件方程式的列立目的要求重点难点导线网条件方程的列立第二章条件平差83-5导线网条件方程式（约45分钟）AD8Y6.BnWB(1)3(n+1) C图3-6如图3-6所示，在这个导线中有四个已知点、n-1个未知点、n+1个水平角观测值和n条边长观测值，总观测值数为2n+1。从图中可以分析，要确定一个未知点的坐标，必须测一条导线边和一个水平角，即需要两个观测值：要确定全部n-1个未知点，则需观测n-1个导线边和n-1个水平角，即必要观测值数t=2n-2：则多余观测个数r=(2n+1)-t=3。也就是说，在单一附合导线中，只有三个条件方程。下面讨论其条件方程式及改正数条件方程式的写法。设AB边方位角已知值为TAs=To，CD边方位角已知值为Tcp、计算值为Tnt1，B点坐标的已知值为(,JB)或者(x1,yi),C点坐标的已知值为(c,Jc)、计算值为(X+,yn+1)。三个条件中，有一个方位角附合条件、两个坐标附合条件。方位角附合条件：从起始方位角推算至终边的方位角平差值应等于其已知值，即Tn+ -Tcp =0(3-3-1纵横坐标附合条件：从起始点推算至终点所得到的坐标平差值应与终点的已知坐标值相等，即X+1-X=0(3-3-2JnI-yc=0(3-3-31.方位角附合条件式↑+ = T。+[β,I* ±(n+1)-180°= T。+[β, +vg J** ±(n+1)-180°则(3-3-1)式可写为Tn/ -Tcp = T +[β, +Ve J* ±(n+1)-180° -Tcp =0第24次第1页

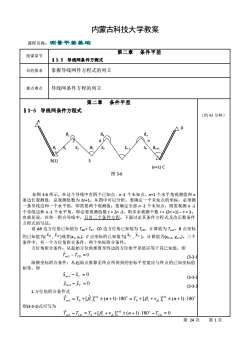
内蒙古科技大学教案 课程名称：测量平差基础 授课章节 第二章 条件平差 §3.5 导线网条件方程式 目的要求 ，掌握导线网件方程式的列立 重点难点 导线网条件方程的列立 第二章 条件平差 §3-5 导线网条件方程式 如图 3-6 所示，在这个导线中有四个已知点、n -1 个未知点、n+1 个水平角观测值和 n 条边长观测值，总观测值数为 2n+1。从图中可以分析，要确定一个未知点的坐标，必须测 一条导线边和一个水平角，即需要两个观测值；要确定全部 n -1 个未知点，则需观测 n -1 个导线边和 n -1 个水平角，即必要观测值数 t = 2n -2；则多余观测个数 r = (2n +1) – t = 3。 也就是说，在单一附合导线中，只有三个条件方程。下面讨论其条件方程式及改正数条件 方程式的写法。 设 AB 边方位角已知值为 TAB = T0，CD 边方位角已知值为 TCD、计算值为 Tn+1，B 点坐标 的已知值为( , )或者(x1, y1)，C 点坐标的已知值为( , )、计算值为(xn+1, yn+1)。三个 条件中，有一个方位角附合条件、两个坐标附合条件。 方位角附合条件：从起始方位角推算至终边的方位角平差值应等于其已知值，即 (3-3-1) 纵横坐标附合条件：从起始点推算至终点所得到的坐标平差值应与终点的已知坐标值 相等，即 (3-3-2) (3-3-3) 1.方位角附合条件式 则(3-3-1)式可写为 整理得 (3-3-4) 其中 （约 45 分钟） 第 24 次 第 1 页 B x B y C x C y 0 ˆ Tn+1 − TCD = x ˆ n+1 − xC = 0 y ˆ n+1 − yC = 0   ] ( 1) 180 [ ] ( 1) 180 ˆ [ ˆ 1 0 1 1 1 0 1 = +  +  = + +  +  + + T + T n T v n n i n n i i   [ ] ( 1) 180 0 ˆ 1 1 − = 0 + + 1  +  − = + + CD n Tn TCD T i v n T i    A D β2 β4 βn 2 4 n β1 S1 S2 β3 S3 Sn-1 Sn βn+1 B(1) 3 (n+1) C 图 3-6

[ve I++ - W =0(3-3-4其中W =-(T。+[β,J+I ±(n+1)-180°-Tcp)2.纵坐标附合条件式终点C坐标平差值表示为Xn+I =X +[AX,]"(3-3-5)而第i边的坐标增量为At, = S, cos T,(3-3-6)式中S, =S, +V's,↑,=T+[β,Ii±i-180°=T+[β, +Ve, i±i-180°=[ve, J +[β,i + T。 ±i-180°=[vp, J + T,其中T,是第i边的近似坐标方位角T, =[β,}"+T±i·180′(3-3-7)做习题约45则（3-3-6）式可表示为分钟Ax, =(S, + Vs, )cos([vp, Ji + T,)上式按泰勒级数展开，取至一次项，得AyiAt, =Ax, + cosT, -Vs.B.JVp"(3-3-8)其中Ax,=S,cosT,，为由观测值计算出的近似坐标增量。(3-3-8)式代入(3-3-5)式，并按vVi合并同类项得nAyiX=XB+Ax, +cosT, Vs+[cos T.-[y=XlP*上式代入（3-3-2）式，整理得1[cosT.Vs]"-[(y, - y,)ve, I" +xn+1 -xc = 0上式即为纵坐标条件方程式，也可写为统一形式：[cosT, -Vs I" -[(yn+-y,)pI"-W,=0P(3-3-9Wx=-(xn+1-Xc）(3-3-103.横坐标附合条件式可以仿照纵坐标条件推导过程（请同学们自己具体推导一下），写出横坐标条件式[sin T Vs J" +[(xn+1 -x,)e I" -w, = 0p(3-3-11W, =-(yn+I -Jc)(3-3-12为使计算方便，保证精度，在实际运算中，S、x、y常以米为单位，W、Vs、ve以厘米为单位，则（3-3-9）和（3-3-11）写为

(3-3-4) 其中 2.纵坐标附合条件式 终点 C 坐标平差值表示为 (3-3-5) 而第 i 边的坐标增量为 (3-3-6) 式中 其中 Ti是第 i 边的近似坐标方位角 (3-3-7) 则（3-3-6）式可表示为 上式按泰勒级数展开，取至一次项，得 (3-3-8) 其中 ，为由观测值计算出的近似坐标增量。 (3-3-8)式代入(3-3-5)式，并按 vβ i合并同类项得 上式代入（3-3-2）式，整理得 上式即为纵坐标条件方程式，也可写为统一形式： (3-3-9) (3-3-10) 3.横坐标附合条件式 可以仿照纵坐标条件推导过程（请同学们自己具体推导一下），写出横坐标条件式 (3-3-11) (3-3-12) 为使计算方便，保证精度，在实际运算中，S、x、y 常以米为单位，w、vS、vβ 以厘米 为单位，则（3-3-9）和（3-3-11）写为 做习题约 45 分钟 [ ] 0 1 1 − = + T n v w i ( [ ] ( 1) 180 ) 1 0 1 CD n wT = − T + i  n +  −T +   n n B i x x x 1 1 ˆ = + [ˆ ] + i Si Ti x ˆ cos ˆ ˆ = Si i i S = S + v ˆ i i i j i i j i i j v T v T i T T i T v i j j j = + = + +   = +   = + +   1 1 1 0 0 1 0 1 [ ] [ ] [ ] 180 ] 180 [ ] 180 ˆ [ ˆ           T = [ ] 1 +T0  i 180 i i  j ˆ ( ) cos([ ] ) 1 i i xi Si vS v T i j  = +  + i i i i i Si j v y x x T v 1 ˆ cos [ ]     =  +  − i Si Ti x = cos n n i n n i S n i i C B i i Si j i i v x T v y y v y x x x T v 1 1 1 1 1 [( ) ] 1 ˆ cos [ ] [cos ]     −  = +  −         = +  +  − + [( ) ] 0 1 [cos ] 1 − 1 + 1 − =   − n+ C n n i n i S T v y y v x x i i  [( ) ] 0 1 [cos ] 1 1 − 1 − =   − + x n n i n Ti vS y y v w i i  ( ) x n 1 C w = − x − x + [( ) ] 0 1 [sin ] 1 1 − 1 − =   + + y n n i n Ti vS x x v w i i  ( ) y n 1 C w = − y − y +

I[cosT,-V's[(y+-y,)I"-w=01SJ2062.65(3-3-131[(x++ -x,)Ve, I" -W, = 0[sin T, - Vs, I'+2062.65(3-3-14综上所述，单一附合导线的平差计算的基本程序是：(1)计算各边近似方位角T,和各点的近似坐标增量值Axi、Ay;(2)参照（3-3-4）写出方位角条件式，参照（3-3-9）、（3-3-10）、（3-3-11)、（3-3-12）或者（3-3-13）、（3-3-14）写出纵横坐标条件方程式；(3)按照条件平差计算的一般程序，计算最或是值并进行精度评定。本次课小结：1．导线网条件方程的列立；2.举例第3页第24次

(3-3-13) (3-3-14) 综上所述，单一附合导线的平差计算的基本程序是： (1)计算各边近似方位角 Ti和各点的近似坐标增量值 Δxi、Δyi； (2)参照（3-3-4）写出方位角条件式，参照（3-3-9）、（3-3-10）、（3-3-11）、（3-3-12）或 者（3-3-13）、（3-3-14）写出纵横坐标条件方程式； (3)按照条件平差计算的一般程序，计算最或是值并进行精度评定。 本次课小结： 1. 导线网条件方程的列立； 2. 举例 第 24 次 第 3 页 [( ) ] 0 2062.65 1 [cos ]  1 − +1 − 1 − x = n n i n Ti vS y y v w i  i [( ) ] 0 2062.65 1 [sin ]  1 + +1 − 1 − y = n n i n Ti vS x x v w i  i