《误差理论及测量平差基础》课程教学资源（授课教案）教案02

?成金娜内素古科技大学INNERMONGOLIAUNIVERSITYOFSCIENCE&TECHNOLOGY教案课程名称测量平差基础总学时数80学时使用班级测绘专 2013-1、2任课学期2014/2015学年第一学期任课教师燕志明编制时间2014年9月3日

教 案 课程名称 测量平差基础 总学时数 80 学 时 使用班级 测绘专 2013-1、2 任课学期 2014/2015 学年第一学期 任课教师 燕志明 编制时间 2014 年 9 月 3 日

内蒙古科技大学教案课程名称：测量平差基础授课章节S1.1偶然误差的概率特性，S1.2衡量精度的指标目的要求了解偶然误差的特性，掌握衡量精度的指标1、偶然误差的概率特性重点难点2、方差和中误差，平均误差、相对误差的基本概念第一章观测误差及其传播引入新课（约2分钟）S1-1偶然误差的规律性任何一个被观测量，客观上总是存在着一个能代表其真正大小的数值。这一数值就称（约10分钟）为该观测量的真值。通常在表示观测值的字母上方加波浪线表示其真值。设进行了n 次观测，各观测值为LI、L2、“、L。，观测量的真值为/.、L、L。由于各观测值都带有一定的误差，所以，每一个观测值的真值（或E(））与观测值之间必存在一个差数，设为A, = L, - L,称一，为真误差（在此仅包含偶然误差），有时简称为误差。若记L-[L L .. ,L-[ , . A-[A, A, .. ,A=L-L则有：如果以被观测值的数学期望表示该观测值的真值E(L)=[E(L)) E(L,) .. E(L,) =[ ,.. , -L△=E(L)-L则有：在此我们用观测值的真值与观测值之差定义真误差，有些教材和文献上用观测值与观测值的真值之差定义真误差。这两种定义方式仅仅是使真误差符号相反，对于后续各种计算公式的推导没有影响。前面已经指出，就单个偶然误差而言，其大小或符号没有规律性，即呈现出一种偶然性（或随机性）。但就其总体而言，却呈现出一定的统计规律性。并且指出它是服从正态分布的随机变量。人们从无数的测量实践中发现，在相同的观测条件下，大量偶然误差的分布也确实表现出了一定的统计规律性。下面用一个实例来说明。在相同的条件下，独立地观测了358个三角形的全部内角，由于观测值带有偶然误差，故三内角观测值之和不等于其真值180°。各个三角形内角和的真误差：A, =180° (L + L, + L),(i= 1,2,,358)式中（L+L+L)）表示各三角形内角和的观测值。现取误差区间的间隔A为0.20”，将这一组误差按其正负号与误差值的大小排列，统计误差出现在各区间内的个数V，以及“误差出现在某个区间内”这一事件的频率"/n（n=358），其结果列于下表中。第2次第1页

内蒙古科技大学教案 课程名称：测量平差基础 授课章节 §1.1 偶然误差的概率特性， §1.2 衡量精度的指标 目的要求 了解偶然误差的特性，掌握衡量精度的指标 重点难点 1、偶然误差的概率特性 2、方差和中误差，平均误差、相对误差的基本概念 第一章 观测误差及其传播 §1-1 偶然误差的规律性 任何一个被观测量，客观上总是存在着一个能代表其真正大小的数值。这一数值就称 为该观测量的真值。通常在表示观测值的字母上方加波浪线表示其真值。 设进行了 n 次观测，各观测值为 L1、 L2、.、Ln，观测量的真值为 、 、. 。 由于各观测值都带有一定的误差，所以，每一个观测值的真值 （或 E( )）与观测值 之间必存在一个差数，设为 称 为真误差（在此仅包含偶然误差），有时简称为误差。若记 ， ， 则有： = 如果以被观测值的数学期望表示该观测值的真值 则有： 在此我们用观测值的真值与观测值之差定义真误差，有些教材和文献上用观测值与观 测值的真值之差定义真误差。这两种定义方式仅仅是使真误差符号相反，对于后续各种计 算公式的推导没有影响。 前面已经指出，就单个偶然误差而言，其大小或符号没有规律性，即呈现出一种偶然 性（或随机性）。但就其总体而言，却呈现出一定的统计规律性。并且指出它是服从正态分 布的随机变量。人们从无数的测量实践中发现，在相同的观测条件下，大量偶然误差的分 布也确实表现出了一定的统计规律性。下面用一个实例来说明。 在相同的条件下，独立地观测了 358 个三角形的全部内角，由于观测值带有偶然误差， 故三内角观测值之和不等于其真值 180º。各个三角形内角和的真误差： 式中 表示各三角形内角和的观测值。现取误差区间的间隔 为 0.20"，将这一组误差按其正负号与误差值的大小排列，统计误差出现在各区间内的个数 ，以及“误差出现在某个区间内”这一事件的频率 （ =358），其结果列于下表中。 表 1-1 某测区三角形内角和的误差分布 4. 观测对象 观测目标本身的结构、状态和清晰程度等，也会对观测结果直接产生影响，如三角测 量中的观测目标觇标和圆筒由于风吹日晒而产生了偏差；GPS 导航定位中的卫星星历误差、 卫星钟误差及设备延迟误差等，都会使测量结果产生误差。 上述的观测者、测量仪器、外界环境及观测对象这四个方面的因素是使测量产生误差 引入新课 （约 2 分钟） （约 10 分钟） 第 2 次 第 1 页 1 ~ L 2 ~ L Ln ~ Li ~ Li Li i = Li − Li ~ i   T n n L L1 L2 . L ,1 =   T n n L L L L ~ . ~ ~ ~ 1 2 ,1 =   T n n  = 1 2 .  ,1  L − L ~ E L E L E L E L  L L L  L T n T n ~ ~ . ~ ~ ( ) ( ) ( ) . ( ) = 1 2 = 1 2 =  = E(L) − L i L L L i 180 ( )  = − 1 + 2 + 3  (i = 1,2,  ,358) L L L i ( ) 1 + 2 + 3 d i v vi / n n

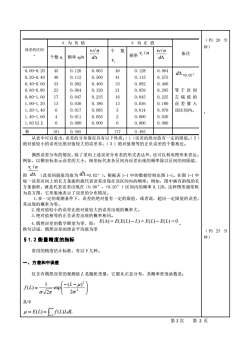
（约20分为负值△为正值钟)误差的区间vilnviln个数频率/n备注4个数vi频率v/nddV0.000.20450.1260. 063460.1280.064d=0. 02"400.200.400.1120.560410.1150.575330.40-0.600.0920.460330.0920.4600.600.80230.0640.320210.0590.295等于区间170.047160.80-1.000.2350.0450.225左端值的1.00-1.20130.0360.180130.0360.180误差算入651.20-1.400.0170.0850.0140.0701该区间内。21.40-1.6040.0110.0550.0060.03000.0000.00000.0001.60以上0.000和1810.5051770.495从表中可以看出，误差的分布情况具有以下性质：（1）误差的绝对值有一定的限值；（2）绝对值较小的误差比绝对值较大的误差多；（3）绝对值相等的正负误差的个数相近。偶然误差分布的情况，除了采用上述误差分布表的形式表达外，还可以利用图形来表达。例如，以横坐标表示误差的大小，纵坐标代表各区间内误差出现的频率除以区间的间隔值，y,/n即d（此处间隔值均取为d△=0.02”）。根据表1-1中的数据绘制出图1-1。在图1-1中每一误差区间上的长方条面积就代表误差出现在该区间内的频率。例如，图中画有斜线的长方条面积，就是代表误差出现在（0.00"，+0.20”）区间内的频率0.128。这种图形通常称为直方图，它形象地表示了误差的分布情况。1.在一定的观测条件下，误差的绝对值有一定的限值，或者说，超出一定限值的误差，其出现的概率为零。2.绝对值较小的误差比绝对值较大的误差出现的概率大。3.绝对值相等的正负误差出现的概率相同。4.偶然误差的数学期望为零，即：E(A)=E(E(L)-L)=E(L)-E(L)=0换句话说，偶然误差的理论平均值为零（约25分钟)81.2衡量精度的指标常用的精度估计标准，有以下几种。一、方差和中误差仅含有偶然误差的观测值L是随机变量，它服从正态分布，其概率密度函数是：(-(L-μ)?)1f(L)=-exp2g20V2元其中(L)LdLμ= E(L) :第2次第2页

从表中可以看出，误差的分布情况具有以下性质：（１）误差的绝对值有一定的限值；（２） 绝对值较小的误差比绝对值较大的误差多；（３）绝对值相等的正负误差的个数相近。 偶然误差分布的情况，除了采用上述误差分布表的形式表达外，还可以利用图形来表达。 例如，以横坐标表示误差的大小，纵坐标代表各区间内误差出现的频率除以区间的间隔值， 即 （此处间隔值均取为 =0.02″）。根据表 1-1 中的数据绘制出图 1-1。在图 1-1 中 每一误差区间上的长方条面积就代表误差出现在该区间内的频率。例如，图中画有斜线的长 方条面积，就是代表误差出现在（0.00″，+0.20″）区间内的频率 0.128。这种图形通常称 为直方图，它形象地表示了误差的分布情况。 1.在一定的观测条件下，误差的绝对值有一定的限值，或者说，超出一定限值的误差， 其出现的概率为零。 2.绝对值较小的误差比绝对值较大的误差出现的概率大。 3.绝对值相等的正负误差出现的概率相同。 4.偶然误差的数学期望为零，即： 。 换句话说，偶然误差的理论平均值为零 §1.2 衡量精度的指标 常用的精度估计标准，有以下几种。 一、方差和中误差 仅含有偶然误差的观测值 L 是随机变量，它服从正态分布，其概率密度函数是：         − − = 2 2 2 ( ) exp 2 1 ( )     L f L 其中  + −  = E(L) = f (L)LdL 误差的区间 ″ Δ 为 负 值 Δ 为 正 值 备注 个数 vi 频率 vi/n 个 数 频率 0.00-0.20 0.20-0.40 0.40-0.60 0.60-0.80 0.80-1.00 1.00-1.20 1.20-1.40 1.40-1.60 1.60 以上 45 40 33 23 17 13 6 4 0 0.126 0.112 0.092 0.064 0.047 0.036 0.017 0.011 0.000 0.063 0.560 0.460 0.320 0.235 0.180 0.085 0.055 0.000 46 41 33 21 16 13 5 2 0 0.128 0.115 0.092 0.059 0.045 0.036 0.014 0.006 0.000 0.064 0.575 0.460 0.295 0.225 0.180 0.070 0.030 0.000 =0.02″ 等于区间 左端值的 误差算入 该区间内。 和 181 0.505 177 0.495 （ 约 20 分 钟） ： （ 约 25 分 钟） 第 2 次 第 2 页 d v n i / d E() = E(E(L) − L) = E(L) − E(L) = 0 d vi/ n i v vi / n d vi/ n d

= D(L) = E([L- E(L)P = [ f(L)[L-E(L)P dL分别是观测值L的数学期望和方差。而L= D(L) = /E[L-E(L)P)称之为观测值L的中误差。由于观测值L和其真值的关系是：L=L+△L=E(L)=μ，所以观测值L的真误差△的概率密度函数是：=E(L)=μ，所以观测值L的真误差△的概率密度函数是：1142(△- E(△)2f() =20202元0/2元2g其中E(A) = f f(A)Ad = 0 = D(A)= E(A- E(A)P)= E()= [ f(A)’dA真误差△的中误差是：= /D(△) = E[- E(A)P /E()可见观测值L的方差、中误差和其真误差△的方差、中误差相同。在相同的测量条件下观测值L和其真误差△的方差计算公式是：ZA-mE2 =D(L)= D(△)= lim月→0>0n1其估计值是A=±nn显然当n→0时，2→？。（约10分钟）二、极限误差若观测值L和其真误差△是仅含有偶然误差的随机变量，并且真误差△服从△～N(0,α）的正态分布，则真误差△出现在各种区间的概率是：P(-<△<)= ff(4)d= 0.683第2次第3页

课       + − L = D L = E L − E L = f L L − E L dL 2 2 2  ( ) ( ) ( ) ( ) 分别是观测值 L 的数学期望和方差。而    2 D(L) E L E(L)  L = = − 称之为观测值 L 的中误差。由于观测值 L 和其真值 L ~ 的关系是： L = L +  ~ ， = ( ) =  ~ L E L ，所以观测值 L 的真误差  的概率密度函数是： = ( ) =  ~ L E L ，所以观测值 L 的真误差  的概率密度函数是：          = −          −   = − 2 2 2 2 2 exp 2 1 2 ( ( )) exp 2 1 ( )       E f 其中 () = ()  = 0  + − E f d       + −  = D  = E  − E  = E  = f   d 2 2 2 2  ( ) ( ) ( ) 真误差  的中误差是： ( )  ( )  ( ) 2 2   = D  = E  − E  ＝ E  可见观测值 L 的方差、中误差和其真误差  的方差、中误差相同。 在相同的测量条件下观测值 L 和其真误差  的方差计算公式是：   n n D L D n i n  =  = =  = → →  ( ) ( ) lim lim 2 2  其估计值是   n n i  =   =   2 ˆ 显然当 n → 时， 2 2  ˆ → 。 二、极限误差 若观测值 L 和其真误差  是仅含有偶然误差的随机变量，并且真误差  服从 (0, ) 2 ～N  的正态分布，则真误差  出现在各种区间的概率是： (−    ) = ()   0.683  + −   P   f d （约 10 分钟） 第 2 次 第 3 页

P(-2α <△<2α)=f(A)d=0.955P(-3α<△<30)= [f(A)d= 0.997一般以2倍或3倍的中误差作为偶然真误差的极限，即限=2(3)注意：极限误差知识真误差的限值，在测量上只有闭合差才是真误差，所以通常把极限误差用作求闭合差的允许值上。三、相对误差（约10分定义：某一物理量观测的中误差与其观测值之比，并归一化，称为这个观测量的相钟)对误差。举例···Aa"Au横向相对误差一=Aα(弧度)=0sAS_Aα"应当：-S0课堂教学小结：1.偶然误差的特性。2.衡量精度的指标。第2次第4页

( 2 2 ) ( ) 0.955 2 2 −    =     + −   P   f d ( 3 3 ) ( ) 0.997 3 3 −    =     + −   P   f d 一般以 2 倍或 3 倍的中误差作为偶然真误差的极限，即 限 ＝2(3) 注意：极限误差知识真误差的限值，在测量上只有闭合差才是真误差，所以通常把极限 误差用作求闭合差的允许值上。 三、相对误差 定义：某一物理量观测的中误差与其观测值之比，并归一化，称为这个观测量的相 对误差。 举例··· 横向相对误差       =   ＝ (弧度)＝ S u 应当：       ＝ S S （约 10 分 钟） 课堂教学小结： 1.偶然误差的特性。 2．衡量精度的指标。 第 2 次 第 4 页