《误差理论及测量平差基础》课程教学资源（授课教案）教案16

?成金娜内素古科技大学INNERMONGOLIAUNIVERSITYOFSCIENCE&TECHNOLOGY教案课程名称测量平差基础总学时数80学时使用班级测绘专 2013-1、2任课学期2014/2015学年第一学期任课教师燕志明编制时间2014年10月27日

教 案 课程名称 测量平差基础 总学时数 80 学 时 使用班级 测绘专 2013-1、2 任课学期 2014/2015 学年第一学期 任课教师 燕志明 编制时间 2014 年 10 月 27 日

内蒙古科技大学教案课程名称：测量平差基础第二章间接平差授课章节82.5间接平差公式汇编及示例目的要求了解间接平差的过程，掌握精度评定。1.间接平差的计算步骤；重点难点2.精度评定。第二章间接平差s2-5间接平差公式汇编及示例（约15分钟）一、公式汇编间接平差的函数模型和随机模型是=BX-1D=0Q=,P平差值方程和误差方程为i=L+V=BX+d或1=L-F(X°)法方程为B'PBX-BPI=O其解为X=(BPB)-BPI=NW观测量和参数的平差值：L=L+V,X=X°+x单位权中误差：VPVvIpV0。=±n-t平差参数X的协方差阵：Dx=60=0N平差参数的函数的协方差阵权函数式：80=FTX协因数：Qa=FQuF=FTNF方差：Dag =OQ第16次第1页

内蒙古科技大学教案 课程名称：测量平差基础 授课章节 第二章 间接平差 §2.5 间接平差公式汇编及示例 目的要求 ，了解间接平差的过程，掌握精度评定。 重点难点 1.间接平差的计算步骤； 2.精度评定。 第二章 间接平差 §2-5 间接平差公式汇编及示例 一、公式汇编 间接平差的函数模型和随机模型是 平差值方程和误差方程为 或 法方程为 其解为 观测量和参数的平差值： 单位权中误差： 平差参数 的协方差阵： 平差参数的函数的协方差阵 权函数式： 协因数： 方差： （约 15 分钟） 第 16 次 第 1 页  = BX −l ~ 2 1 0 2 0 − D = Q = P L = L+V = BX + d ˆ ˆ ( ) 0 l = L − F X B PBx ˆ − B Pl = 0 T T x B PB B Pl NbbW T 1 T 1 ˆ ( ) − − = = L L V X X x ˆ ˆ , ˆ 0 = + = + n t V PV r V PV T T − ˆ 0 =  =  X ˆ 2 1 ˆ ˆ 0 2 ˆ ˆ 0 ˆ ˆ − DXX = QXX = Nbb F x T  ˆ = ˆ Q F Q F F Nb b F T XX T 1 ˆ ˆ ˆ ˆ −  = =   ˆˆ 2 ˆ ˆ 0 D = ˆ Q

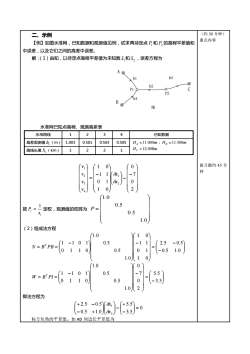
（约30分钟）二、示例重点内容【例】如图水准网，已知数据和观测值见例，试求两待定点P和P，的高程平差值和中误差，以及它们之间的高差中误差。解：（1）由知，以待定点高程平差值为未知数，和，，误差方程为A&h3yhl?h2CP1 8P2h4B&图水准网已知点高程、观测高差表12水准路线3已知数据4高差观测值h，（m）1.0030.5010.5030.505H,=11.000m,Hg=11.500mHc=12.008m2112路线长度S，（km）做习题约45分0(01Vi钟71ax1V2001dxV3（210V4(1.00.5一定权，观测值的权阵为P=按P=0.5Si1.0)（2）组成法方程(1.0丫10)-1 1(2.5(1-1 0 1)0.50.5)N= B'PB--110010.5(-0.51.0(01.0八10Y。)(1.0(1-101)-7(5.5)0.5W=B"PI-1100(-3.5)O0.521.0八即法方程为(+5.5)(+2.5-0.5a= 0-0.5+1.0x(-3.5)标方位角的平差值。如AD间边长平差值为

二、示例 【例】如图水准网，已知数据和观测值见例，试求两待定点 P1 和 P2 的高程平差值和 中误差，以及它们之间的高差中误差。 解：（1）由知，以待定点高程平差值为未知数 1 x ˆ 和 2 x ˆ ，误差方程为 水准网已知点高程、观测高差表 水准路线 1 2 3 4 已知数据 高差观测值 i h （m） 1.003 0.501 0.503 0.505 HA =11.000m， HB =11.500m 路线长度 HC =12.008m i S （km） 1 2 2 1               − −                      − =               2 0 7 0 1 0 0 1 1 1 1 0 2 1 4 3 2 1 x x v v v v   按 i i s P 1 = 定权，观测值的权阵为               = 1.0 0.5 0.5 1.0 P （2）组成法方程         − − =               −                       − = = 0.5 1.0 2.5 0.5 1 0 0 1 1 1 1 0 1.0 0.5 0.5 1.0 0 1 1 0 1 1 0 1 N B PB T         − =               −                       − = = 3.5 5.5 2 0 7 0 1.0 0.5 0.5 1.0 0 1 1 0 1 1 0 1 W B Pl T 即法方程为 0 3.5 5.5 0.5 1.0 2.5 0.5 2 1 =        − + −                − + + − x x   标方位角的平差值。如 AD 间边长平差值为 （约 30 分钟） 重点内容 做习题约 45 分 钟 B A h2 P1 h4 h1 P2 h3 C 图

（3）求解法方程未知数协因数矩阵+2.5-0.5)-(0.44440.2222Qx = N-I(o.22221.1111)-0.5+1.0)于是未知数的解：dx.(0.44440.2222)+5.5)(+1.670.22221.1111-2.67)-3.5dx,（4）将未知数的值代入误差方程，改正数为0（0)(+1.67)y1(+1.67)+ 2.67-7V2 2.67-2.670V320.33V0（5）计算单位权中误差[pv]10.02672.24(mm)mo=V4-2Vn-t"（6）计算待定点P和P,的高程及高程中误差Hpl=x= x°+&x,=12.003+0.00167=12.0047(m)Hp2=x=x+&x,=12.511-0.00267=12.5083(m)根据式（2一4一6）求待定点高程中误差：mpl=mo/m=2.24×/0.4444=1.49(mm)mp2 = mo /Om=2.24×/1.1111 =2.36 (mm)（7）P和P,的高差中误差由图可知，高差平差值函数式为h, =-x, +x, =(-1这里，P、P,点间高差的平差值是未知数的线性函数，未知数的系数与权函数系数相同，直接应用（2—4—11）式，计算其协因数(0.44440.2222)Qin2=f'OJ =(-1 =1.1(0.22221.1111)由式计算高差中误差miz2= mo /Qiz = 2.24×1.11= 2.48 (mm)

（3）求解法方程 未知数协因数矩阵         =         − + + − = = − − 0.2222 1.1111 0.4444 0.2222 0.5 1.0 2.5 0.5 1 1 Q ˆ ˆ N XX 于是未知数的解：         − + =        − +         =        2.67 1.67 3.5 5.5 0.2222 1.1111 0.4444 0.2222 2 1 x x   （4）将未知数的值代入误差方程，改正数为               − − + + =               − −        − +               − =               0.33 2.67 2.67 1.67 2 0 7 0 2.67 1.67 1 0 0 1 1 1 1 0 4 3 2 1 v v v v ； （5）计算单位权中误差 2.24 4 2 [ ] 10.0267 0 = − = − = n t pvv m （mm） ‘（6）计算待定点 P1 和 P2 的高程及高程中误差 ˆ 12.003 0.00167 12.0047 ˆ 1 0 HP1 = x1 = x1 + x = + = （m） ˆ 12.511 0.00267 12.5083 ˆ 2 0 HP2 = x2 = x2 + x = − = （m） 根据式（2—4—6）求待定点高程中误差： 2.24 0.4444 1.49 1 0 1 1 mP = m Qx x =  = （mm） 2.24 1.1111 2.36 2 0 2 2 mP = m Qx x =  = （mm） （7） P1 和 P2 的高差中误差 由图可知，高差平差值函数式为 ( ) f X x x h x x T ˆ ˆ ˆ ˆ ˆ 1 1 ˆ 2 1 2 1 2 =        = − + = − 这里， P1 、 P2 点间高差的平差值是未知数的线性函数，未知数的系数与权函数系数 相同，直接应用（2—4—11）式，计算其协因数 ( ) 1.11 1 1 0.2222 1.1111 0.4444 0.2222 ˆ ˆ 1 1 2 ˆ =       −         Q = f Q f = − XX T h 由式计算高差中误差 2.24 1.11 2.48 2 0 ˆ 2 ˆ = =  = h h m m Q （mm）

本次课小结：1.公式汇编；2.示例；第16次第3页

本次课小结： 1. 公式汇编 ； 2. 示例 ； 第 16 次 第 3 页