《误差理论及测量平差基础》课程教学资源（授课教案）教案00

#博童##事成金娜内古科技大学INNERMONGOLIAUNIVERSITYOFSCIENCE&TECHNOLOGY教案课程名称误差理论与测量平差基础总学时数64学时使用班级测绘 2013-1、2任课学期2014/2015学年第一学期任课教师孙同贺编制时间2014年9月4日

教 案 课程名称 误差理论与测量平差基础 总学时数 64 学 时 使用班级 测绘 2013-1、2 任课学期 2014/2015 学年第一学期 任课教师 孙同贺 编制时间 2014 年 9 月 4 日

内蒙古科技大学教案课程名称：误差理论与测量平差基础第一章绪论授课章节$1.1观测误差$1.2测量平差学科的研究对象目的要求了解测量平差的任务，掌握误差的分类。1、测量条件重点难点2、系统误差和粗差的定义和区别绪论引入新课1.1观测误差（约5分钟）在测量工作中，由于受测量过程中客观存在的各种因素影响，使得一切测量结果都不可避免地带有误差。例如，对一段距离进行重复观测时，各次观测的长度总不可能完全相同。又如，一个平面三角形三内角之和理论上应等于180°，实际上，如果对这三个内角进行观测，其三内角观测值之和一般不等于180°，而存有差异，这种差异的产生，是因为观测值中含有观测误差。于是，研究观测误差的内在规律，对带有误差的观测数据进行数学处理并评定其精确程度等，就成为测量工作中需要解决的重要实际问题。一、误差来源观测误差产生的原因很多，概括起来主要有以下四个方面。观测误差的来1.观测者源讲解由于观测者的感觉器官的鉴别能力有一定的局限性，因此在仪器的安置、照准、读数（约20分钟）等方面都会产生误差。同时，观测者的工作态度、技术水平以及情绪的变化，也会对观测成果的质量产生影响。2.测量仪器测量是利用测量仪器进行的，由于测量仪器结构的不完善，测量的精密度有一定的限度，因而使观测值产生误差。例如，光学经纬仪，理论上要求主光轴、俯仰轴和垂直轴三轴要正交，但实际上不可能严格正交：水准仪的视准轴不平行于水准轴：电磁波测距仪的零位误差、电路延迟：经纬仪、测距仪度盘的刻划误差等，这些因素都会使测量结果产生误差。3.外界环境观测过程所处的客观环境，如温度、湿度、风力、风向、大气折光、电离层延迟等因素都会对观测结果产生影响；同时，随着这些因素的变化，如温度的高低，湿度的大小，风力的强弱及大气折光的不同，其对观测结果的影响也不同。在这种多样而变化的外界自然条件下进行观测，就必然使观测结果产生误差4.观测对象观测目标本身的结构、状态和清晰程度等，也会对观测结果直接产生影响，如三角测量中的观测目标标和圆筒由于风吹日晒而产生了偏差：GPS导航定位中的卫星星历误差、卫星钟误差及设备延迟误差等，都会使测量结果产生误差

内蒙古科技大学教案 课程名称：误差理论与测量平差基础 授课章节 第一章 绪论 §1.1 观测误差 §1.2 测量平差学科的研究对象 目的要求 了解测量平差的任务，掌握误差的分类。 重点难点 1、测量条件 2、系统误差和粗差的定义和区别 绪 论 1.1 观测误差 在测量工作中，由于受测量过程中客观存在的各种因素影响，使得一切测量结果都不 可避免地带有误差。例如，对一段距离进行重复观测时，各次观测的长度总不可能完全相 同。又如，一个平面三角形三内角之和理论上应等于 180°，实际上，如果对这三个内角 进行观测，其三内角观测值之和一般不等于 180°，而存有差异，这种差异的产生，是因 为观测值中含有观测误差。于是，研究观测误差的内在规律，对带有误差的观测数据进行 数学处理并评定其精确程度等，就成为测量工作中需要解决的重要实际问题。 一、误差来源 观测误差产生的原因很多，概括起来主要有以下四个方面。 1. 观测者 由于观测者的感觉器官的鉴别能力有一定的局限性，因此在仪器的安置、照准、读数 等方面都会产生误差。同时，观测者的工作态度、技术水平以及情绪的变化，也会对观测 成果的质量产生影响。 2. 测量仪器 测量是利用测量仪器进行的，由于测量仪器结构的不完善，测量的精密度有一定的限 度，因而使观测值产生误差。例如，光学经纬仪，理论上要求主光轴、俯仰轴和垂直轴三 轴要正交，但实际上不可能严格正交；水准仪的视准轴不平行于水准轴；电磁波测距仪的 零位误差、电路延迟；经纬仪、测距仪度盘的刻划误差等，这些因素都会使测量结果产生 误差。 3. 外界环境 观测过程所处的客观环境，如温度、湿度、风力、风向、大气折光、电离层延迟等因 素都会对观测结果产生影响；同时，随着这些因素的变化，如温度的高低，湿度的大小， 风力的强弱及大气折光的不同，其对观测结果的影响也不同。在这种多样而变化的外界自 然条件下进行观测，就必然使观测结果产生误差。 4. 观测对象 观测目标本身的结构、状态和清晰程度等，也会对观测结果直接产生影响，如三角测 量中的观测目标觇标和圆筒由于风吹日晒而产生了偏差；GPS 导航定位中的卫星星历误差、 卫星钟误差及设备延迟误差等，都会使测量结果产生误差。 三、本课程的主要内容 由测量平差的基本概念可知，测量平差的主要任务有两个，一是依最小二乘原理求出 待定量的最可靠值，二是评定观测结果和平差结果的精度。本课程《误差理论与测量平差》 的主要任务是系统介绍最小二乘法与测量平差的基本理论和基本方法，为以后的专业课学 引入新课 （约 5 分钟） 观测误差的来 源讲解 （约 20 分钟）

二、观测误差分类根据观测误差对测量结果的影响性质，可分为偶然误差、系统误差和粗差三类。1.粗差粗差主要是由失误引起的，一般以异常值或孤值形式表现出来。如测错、读错、记录错、计算错、仪器故障等所引起的偏差。经典测量中，这类粗差一般采取变更仪器或操作程序、重复观测和检核验算、分析等方式，检出粗差并予以剔除。因此，可以认为观测值中已基本没有粗差。现代测量中，观测过程中的电子化、自动化程度日益提高，观测数据自动记录、自动传输和计算，粗差的检测和分析，已成为一个重要问题。所以，在观测方案的设计和实施、观测中的检核及测后的分析处理中，采取有效措施进行粗差的探测和消除，是非常重要的。重点：2.系统误差系统误差及其由测量条件中某些特定因素的系统性影响而产生的误差称为系统误差。同等测量条下减弱或消除的措施讲解的一系列观测中，系统误差的大小和符号常固定不变，或呈系统性变化。对于一定的测量（约20分条件和作业程序，系统误差在数值上服从一定的函数性规律。3.偶然误差重点：由测量条件中各种随机因素的偶然性影响而产生的误差称为偶然误差。偶然误差的出偶然误差讲解现，就单个而言，无论数值和符号，都无规律性，而对于大量误差的总体，却存在一定的（约10分钟）统计规律。1.2测量平差学科的研究对象测量平差的主要任务有两个，一是依最小二乘原理求出待定量的最可靠值，二是评定（约35分钟）观测结果和平差结果的精度。本课程的主要内容本课程《误差理论及测量平差》的主要任务是系统介绍最小二乘法与测量平差的基本理论和基本方法，为以后的专业课学习，及进一步学习和研究测量平差打下坚实基础。其主要内容为：（1）偶然误差理论。包括偶然误差的概率特性，精度指标，中误差和权的定义，方差阵及权逆阵传播规律等。（2）测量平差函数模型和随机模型的概念及建立，参数估计概念及最小二乘原理。（3）测量平差基本方法。介绍条件平差方法、附有未知参数的条件平差方法：间接平差、具有条件的间接平差方法等。（4）测量数据的统计假设检验方法。课堂教学小结：1、由茂入廉，由近及远，便于学生在已有知识的基融上理解，2.测量误差的来源3余误差偶然误差的性质，乐统误差消除或减弱的方法；4.本保程的任务及内客

二、观测误差分类 根据观测误差对测量结果的影响性质，可分为偶然误差、系统误差和粗差三类。 1. 粗差 粗差主要是由失误引起的，一般以异常值或孤值形式表现出来。如测错、读错、记录 错、计算错、仪器故障等所引起的偏差。经典测量中，这类粗差一般采取变更仪器或操作 程序、重复观测和检核验算、分析等方式，检出粗差并予以剔除。因此，可以认为观测值 中已基本没有粗差。现代测量中，观测过程中的电子化、自动化程度日益提高，观测数据 自动记录、自动传输和计算，粗差的检测和分析，已成为一个重要问题。所以，在观测方 案的设计和实施、观测中的检核及测后的分析处理中，采取有效措施进行粗差的探测和消 除，是非常重要的。 2. 系统误差 由测量条件中某些特定因素的系统性影响而产生的误差称为系统误差。同等测量条下 的一系列观测中，系统误差的大小和符号常固定不变，或呈系统性变化。对于一定的测量 条件和作业程序，系统误差在数值上服从一定的函数性规律。 3. 偶然误差 由测量条件中各种随机因素的偶然性影响而产生的误差称为偶然误差。偶然误差的出 现，就单个而言，无论数值和符号，都无规律性，而对于大量误差的总体，却存在一定的 统计规律。 1.2 测量平差学科的研究对象 测量平差的主要任务有两个，一是依最小二乘原理求出待定量的最可靠值，二是评定 观测结果和平差结果的精度。 本课程的主要内容 本课程《误差理论及测量平差》的主要任务是系统介绍最小二乘法与测量平差的基本 理论和基本方法，为以后的专业课学习，及进一步学习和研究测量平差打下坚实基础。其 主要内容为： （1）偶然误差理论。包括偶然误差的概率特性，精度指标，中误差和权的定义，方差 阵及权逆阵传播规律等。 （2）测量平差函数模型和随机模型的概念及建立，参数估计概念及最小二乘原理。 （3）测量平差基本方法。介绍条件平差方法、附有未知参数的条件平差方法；间接平 差、具有条件的间接平差方法等。 （4）测量数据的统计假设检验方法。 最后简要介绍一些现代测量平差理论和方法，以便与以后的测量平差课程相连接，为进一 步学习和研究这种理论和方法打下基础 重点： 系统误差及其 减弱或消除的 措施讲解 （约 20 分 重点： 偶然误差讲解 （约 10 分钟） （约 35 分钟） ） 课堂教学小结： 1、由浅入深，由近及远，便于学生在已有知识的基础上理解； 2．测量误差的来源； 3．系统误差、偶然误差的性质，系统误差消除或减弱的方法； 4.本课程的任务及内容

内蒙古科技大学教案第二章误差分布与精度指标授课章节$2.3偶然误差的概率特性$2.4衡量精度的指标目的要求了解偶然误差的特性，掌握衡量精度的指标1、偶然误差的概率特性重点难点2、方差和中误差，平均误差、相对误差的基本概念2.3偶然误差的规律性任何一个被观测量，客观上总是存在着一个能代表其真正大小的数值。这一数值就称为该观引入新课测量的真值。通常在表示观测值的字母上方加波浪线表示其真值。（约2分钟）设进行了n次观测，各观测值为L、L2、…、L，观测量的真值为L、L、.L。由于各观测值都带有一定的误差，所以，每一个观测值的真值，（或E（L））与观测值L之间必存在一个（约10分钟）差数，设为A, = L, - L,称，为真误差（在此仅包含偶然误差)，有时简称为误差。若记-[.-[,. -[A.,△= L-L则有：如果以被观测值的数学期望表示该观测值的真值E(L)-[E(L) E(L) ... E(L,) =[Z L,.. ,J - L△=E(L)-L则有：在此我们用观测值的真值与观测值之差定义真误差，有些教材和文献上用观测值与观测值的真值之差定义真误差。这两种定义方式仅仅是使真误差符号相反，对于后续各种计算公式的推导没有影响。前面已经指出，就单个偶然误差而言，其大小或符号没有规律性，即呈现出一种偶然性（或随机性）。但就其总体而言，却呈现出一定的统计规律性。并且指出它是服从正态分布的随机变量。人们从无数的测量实践中发现，在相同的观测条件下，大量偶然误差的分布也确实表现出了一定的统计规律性。下面用一个实例来说明。在相同的条件下，独立地观测了358个三角形的全部内角，由于观测值带有偶然误差，故三内角观测值之和不等于其真值180°。各个三角形内角和的真误差：A, =180° (L + L, + L), (i=1,2,,358)式中(L+L,+L):表示各三角形内角和的观测值。现取误差区间的间隔d△为0.20，将这一组误差按其正负号与误差值的大小排列，统计误差出现在各区间内的个数"i，以及“误差出现在某个区间内”这一事件的频率V,/n（n=358），其结果列于下表中

内蒙古科技大学教案 授课章节 第二章 误差分布与精度指标 §2.3 偶然误差的概率特性 §2.4 衡量精度的指标 目的要求 了解偶然误差的特性，掌握衡量精度的指标 重点难点 1、偶然误差的概率特性 2、方差和中误差，平均误差、相对误差的基本概念 2.3 偶然误差的规律性 任何一个被观测量，客观上总是存在着一个能代表其真正大小的数值。这一数值就称为该观 测量的真值。通常在表示观测值的字母上方加波浪线表示其真值。 设进行了 n 次观测，各观测值为 L1、 L2、.、Ln，观测量的真值为 1 ~ L 、 2 ~ L 、. Ln ~ 。由于各观 测值都带有一定的误差，所以，每一个观测值的真值 Li ~ （或 E( Li )）与观测值 Li 之间必存在一个 差数，设为 i = Li − Li ~ 称 i 为真误差（在此仅包含偶然误差），有时简称为误差。若记   T n n L L1 L2 . L ,1 = ，   T n n L L L L ~ . ~ ~ ~ 1 2 ,1 = ，   T n n  = 1 2 .  ,1 则有：  = L − L ~ 如果以被观测值的数学期望表示该观测值的真值 E L E L E L E L  L L L  L T n T n ~ ~ . ~ ~ ( ) ( ) ( ) . ( ) = 1 2 = 1 2 = 则有：  = E(L) − L 在此我们用观测值的真值与观测值之差定义真误差，有些教材和文献上用观测值与观测值的 真值之差定义真误差。这两种定义方式仅仅是使真误差符号相反，对于后续各种计算公式的推导 没有影响。 前面已经指出，就单个偶然误差而言，其大小或符号没有规律性，即呈现出一种偶然性（或 随机性）。但就其总体而言，却呈现出一定的统计规律性。并且指出它是服从正态分布的随机变量。 人们从无数的测量实践中发现，在相同的观测条件下，大量偶然误差的分布也确实表现出了一定 的统计规律性。下面用一个实例来说明。 在相同的条件下，独立地观测了 358 个三角形的全部内角，由于观测值带有偶然误差，故三 内角观测值之和不等于其真值 180º。各个三角形内角和的真误差： i L L L i 180 ( )  = − 1 + 2 + 3  (i = 1,2,  ,358) 式中 L L L i ( ) 1 + 2 + 3 表示各三角形内角和的观测值。现取误差区间的间隔 d 为 0.20"，将这 一组误差按其正负号与误差值的大小排列，统计误差出现在各区间内的个数 i v ，以及“误差出现 在某个区间内”这一事件的频率 vi / n （ n =358），其结果列于下表中。 引入新课 （约 2 分钟） （约 10 分钟）

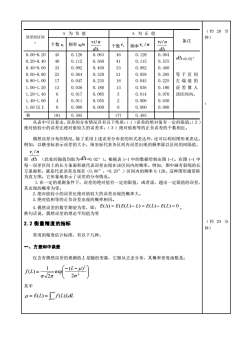
（约20分△为负值为正值误差的区间钟)备注vilnvi/nM个数vi频率v/n频率V/n个数\idada0. 000.20450. 126460.1280.0630. 064d=0. 02"400.560410.5750.20-0.400. 1120.1150. 40-0. 60330.0920.460330.0920.4600.60-0.80230.0640.320210.0590.295等于区间170.047160.0450.80-1.000.2350.225左端值的1.00-1.20130.0360.180130.0360.180误差算入1.20-1.4060.0170.08550.0140.070该区间内。1.40-1.6040.01120.0060.0300.05500.00001.60以上0.0000.0000.000和1771810.5050.495从表中可以看出，误差的分布情况具有以下性质：（1）误差的绝对值有一定的限值：（2绝对值较小的误差比绝对值较大的误差多；（3）绝对值相等的正负误差的个数相近。偶然误差分布的情况，除了采用上述误差分布表的形式表达外，还可以利用图形来表达。例如，以横坐标表示误差的大小，纵坐标代表各区间内误差出现的频率除以区间的间隔值，y,/n即d（此处间隔值均取为d△=0.02"）。根据表1-1中的数据绘制出图1-1。在图1-1中每一误差区间上的长方条面积就代表误差出现在该区间内的频率。例如，图中画有斜线的长方条面积，就是代表误差出现在（0.00”，+0.20”）区间内的频率0.128。这种图形通常称为直方图，它形象地表示了误差的分布情况。1.在一定的观测条件下，误差的绝对值有一定的限值，或者说，超出一定限值的误差，其出现的概率为零。2.绝对值较小的误差比绝对值较大的误差出现的概率大。3.绝对值相等的正负误差出现的概率相同。4. 偶然误差的数学期望为零，即：E(A)=E(E(L)-L)=E(L)-E(L)=0。换句话说，偶然误差的理论平均值为零（约25分2.2衡量精度的指标钟)常用的精度估计标准，有以下几种。一、方差和中误差仅含有偶然误差的观测值L是随机变量，它服从正态分布，其概率密度函数是：1(-(L-μ)F(L) =exp2α20/2元其中(L)LdLμ= E(L)

误差的区间 ″ Δ 为 负 值 Δ 为 正 值 备注 个数 vi 频率 vi/n d vi/ n 个数 i v 频率 vi / n d vi/ n 0.00-0.20 0.20-0.40 0.40-0.60 0.60-0.80 0.80-1.00 1.00-1.20 1.20-1.40 1.40-1.60 1.60 以上 45 40 33 23 17 13 6 4 0 0.126 0.112 0.092 0.064 0.047 0.036 0.017 0.011 0.000 0.063 0.560 0.460 0.320 0.235 0.180 0.085 0.055 0.000 46 41 33 21 16 13 5 2 0 0.128 0.115 0.092 0.059 0.045 0.036 0.014 0.006 0.000 0.064 0.575 0.460 0.295 0.225 0.180 0.070 0.030 0.000 d =0.02″ 等于区间 左端值的 误差算入 该区间内。 和 181 0.505 177 0.495 从表中可以看出，误差的分布情况具有以下性质：（１）误差的绝对值有一定的限值；（２） 绝对值较小的误差比绝对值较大的误差多；（３）绝对值相等的正负误差的个数相近。 偶然误差分布的情况，除了采用上述误差分布表的形式表达外，还可以利用图形来表达。 例如，以横坐标表示误差的大小，纵坐标代表各区间内误差出现的频率除以区间的间隔值， 即 d v n i / （此处间隔值均取为 d =0.02″）。根据表 1-1 中的数据绘制出图 1-1。在图 1-1 中 每一误差区间上的长方条面积就代表误差出现在该区间内的频率。例如，图中画有斜线的长 方条面积，就是代表误差出现在（0.00″，+0.20″）区间内的频率 0.128。这种图形通常称 为直方图，它形象地表示了误差的分布情况。 1.在一定的观测条件下，误差的绝对值有一定的限值，或者说，超出一定限值的误差， 其出现的概率为零。 2.绝对值较小的误差比绝对值较大的误差出现的概率大。 3.绝对值相等的正负误差出现的概率相同。 4.偶然误差的数学期望为零，即： E() = E(E(L) − L) = E(L) − E(L) = 0 。 换句话说，偶然误差的理论平均值为零 2.2 衡量精度的指标 常用的精度估计标准，有以下几种。 一、方差和中误差 仅含有偶然误差的观测值 L 是随机变量，它服从正态分布，其概率密度函数是：         − − = 2 2 2 ( ) exp 2 1 ( )     L f L 其中  + −  = E(L) = f (L)LdL （ 约 20 分 钟） ： （ 约 25 分 钟）

= D(L) = E(z - E(L)P )= f f(L)[L- E(L)P dL分别是观测值L的数学期望和方差。而0/ = /D(L) = VE(L- E(L)P)称之为观测值L的中误差。由于观测值L和其真值L的关系是：L=L+△，L=E(L)=μ，所以观测值L的真误差△的概率密度函数是：L=E(L)=μ，所以观测值L的真误差△的概率密度函数是：142(△- E(A)2f(△) =expeXD2g2g/2元2g0V2元其中E(A) = Jr (A)Ad = 0 = D(A) = E[A-E(A)P )= E()= r f(A)4dA真误差△的中误差是：= /D(A) =/E([△-E(A)P/E(4")可见观测值L的方差、中误差和其真误差△的方差、中误差相同。在相同的测量条件下观测值L和其真误差△的方差计算公式是：ZA- lim [M]2 = D(L) = D(△)= limlmnnn-→0n其估计值是A[A]=nn显然当n→时，2→。（约10分钟）二、极限误差若观测值L和其真误差△是仅含有偶然误差的随机变量，并且真误差△服从△N(0,α"）的正态分布，则真误差△出现在各种区间的概率是：P(-α<<0)= [tf(A)d~ 0.683

课       + − L = D L = E L − E L = f L L − E L dL 2 2 2  ( ) ( ) ( ) ( ) 分别是观测值 L 的数学期望和方差。而    2 D(L) E L E(L)  L = = − 称之为观测值 L 的中误差。由于观测值 L 和其真值 L ~ 的关系是： L = L +  ~ ， = ( ) =  ~ L E L ，所以观测值 L 的真误差  的概率密度函数是： = ( ) =  ~ L E L ，所以观测值 L 的真误差  的概率密度函数是：          = −          −   = − 2 2 2 2 2 exp 2 1 2 ( ( )) exp 2 1 ( )       E f 其中 () = ()  = 0  + − E f d       + −  = D  = E  − E  = E  = f   d 2 2 2 2  ( ) ( ) ( ) 真误差  的中误差是： ( )  ( )  ( ) 2 2   = D  = E  − E  ＝ E  可见观测值 L 的方差、中误差和其真误差  的方差、中误差相同。 在相同的测量条件下观测值 L 和其真误差  的方差计算公式是：   n n D L D n i n  =  = =  = → →  ( ) ( ) lim lim 2 2  其估计值是   n n i  =   =   2 ˆ 显然当 n → 时， 2 2  ˆ → 。 二、极限误差 若观测值 L 和其真误差  是仅含有偶然误差的随机变量，并且真误差  服从 (0, ) 2 ～N  的正态分布，则真误差  出现在各种区间的概率是： (−    ) = ()   0.683  + −   P   f d （约 10 分钟）

P(-2g <<20) = Jtz f(A)d△~ 0.955P(-3g<△<30)= ftg f(A)dA ~ 0.997一般以2倍或3倍的中误差作为偶然真误差的极限，即△限=2(3)o注意：极限误差知识真误差的限值，在测量上只有闭合差才是真误差，所以通常把极限误差用作求闭合差的允许值上。三、相对误差（约10分定义：某一物理量观测的中误差与其观测值之比，并归一化，称为这个观测量的相钟)对误差。举例···=Aα(弧度)=α"横向相对误差=usp"AS_Aa"应当：sp"课堂教学小结：1.偶然误差的特性。2.衡量精度的指标

( 2 2 ) ( ) 0.955 2 2 −    =     + −   P   f d ( 3 3 ) ( ) 0.997 3 3 −    =     + −   P   f d 一般以 2 倍或 3 倍的中误差作为偶然真误差的极限，即 限 ＝2(3) 注意：极限误差知识真误差的限值，在测量上只有闭合差才是真误差，所以通常把极限 误差用作求闭合差的允许值上。 三、相对误差 定义：某一物理量观测的中误差与其观测值之比，并归一化，称为这个观测量的相 对误差。 举例··· 横向相对误差       =   ＝ (弧度)＝ S u 应当：       ＝ S S （约 10 分 钟） 课堂教学小结： 1.偶然误差的特性。 2．衡量精度的指标

内蒙古科技大学教案第三章协方差转播律及权授课章节$3.1协方差转播律目的要求了解什么是协方差传播，掌握协方差传播率及其在实践的应用。1、方差传播定律的理论推导重点难点2、方差传播定律线性函数的方差在实际工作中，一些未知量的求得，常常不是依靠直接测定或不可能直接测定，而是要通过由观测值所组成的函数计算解出。如，平面三角形闭合差W就是通过三个内角的观引入新课测值计算所得，即w=180°-L，+L，+L）。闭合差w无法直接测出。（约10分钟）又如，在三角形 ABC中，已测得两个角A、B及一条边a，则依b=“siB求求b边sin A时，也是通过观测值计算函数b。[，要由观测值算出。再如，一个量n次等精度观测值的中数x=n上面的W、b及x，都是观测值的函数。显然，由观测值计算所得函数值的精确与否，主要取决于作为自变量的观测值的质量好坏。一般地说，自变量带有的误差，必然以一定规律传播给函数值，所以对这样求得的函数值，也有个精度估计的问题。即由具有一定中误差的自变量计算所得的函数值，也应具有相应的中误差。这种一些量的中误差与这些量组成的函数的中误差之间的关系式，称为误差传播律。因为中误差的平方是方差的估值，所以中误差的传播关系可以通过方差和协方差的运算规律来导出。3.1协方差的传播一、观测值线性函数的方差设随机向量X，其自协方差阵是Dxx；又假设有X的线性函数是z=KX+ko，其（约35分钟）中K和k已知，K=(k,kz,",kn)。由于Az = KAX=> A- = K(AXAXT)那么z的方差是? = E(4-")= E[(=- E(2)]- E[K(4XAXT)KT]= KE(AXAX')KI = KDxKT

内蒙古科技大学教案 授课章节 第三章 协方差转播律及权 §3.1 协方差转播律 目的要求 了解什么是协方差传播，掌握协方差传播率及其在实践的应用。 重点难点 1、 方差传播定律的理论推导 2、 方差传播定律线性函数的方差 在实际工作中，一些未知量的求得，常常不是依靠直接测定或不可能直接测定，而是 要通过由观测值所组成的函数计算解出。如，平面三角形闭合差 w 就是通过三个内角的观 测值计算所得，即 ( ) 1 2 3 0 w = 180 − L + L + L 。闭合差 w 无法直接测出。 又如，在三角形 ABC 中，已测得两个角 A 、 B 及一条边 a ，则依 A a B b sin sin = 求 b 边 时，也是通过观测值计算函数 b 。 再如，一个量 n 次等精度观测值的中数   n L x = ，要由观测值算出。 上面的 W 、b 及 x ，都是观测值的函数。显然，由观测值计算所得函数值的精确与否， 主要取决于作为自变量的观测值的质量好坏。一般地说，自变量带有的误差，必然以一定 规律传播给函数值，所以对这样求得的函数值，也有个精度估计的问题。即由具有一定中 误差的自变量计算所得的函数值，也应具有相应的中误差。这种一些量的中误差与这些量 组成的函数的中误差之间的关系式，称为误差传播律。 因为中误差的平方是方差的估值，所以中误差的传播关系可以通过方差和协方差的运 算规律来导出。 3.1 协方差的传播 一、观测值线性函数的方差 设随机向量 n1 X ，其自协方差阵是 DXX ；又假设有 n1 X 的线性函数是 0 1 1 z K X k n n = +   ，其 中 K 和 0 k 已知， ( , , , ) 1 2 n K = k k  k 。 由于 z = KX ＝＞ T T z K( X X )K 2  =   那么 z 的方差是 ( )    T XX T T T T z KE X X K KD K E z E z E z E K X X K =   = =  = − =   ( ) ( ) ( ) ( ) 2 2 2  引入新课 （约 10 分钟） （约 35 分钟）

而OOxOO x2x,Dxx =.....CiO..O当自变量(，x2，,x）相互独立时，有o0..0。x,Dxx =0o...0此时ko9?=1=1【例题1】在1:500的地图上，量得某两点间的距离是d=23.4mm，d的量距误差是（约10分钟）Oa=±0.2mm。求两点间的实地距离S和其精度s。解：S=500d=500×23.4=11700mm=11.7ms=500ga=500×(±0.2)=±100mm=±0.1m最后写成S=11.7m±0.1m2【例题2】设x是独立观测值L、L,和L,的函数，即：x=已知L7172L,和L,的中误差是,=±3mm、，=±2mm和o；=±lmm，求函数x的精度。解：因为L、L,和L,是独立观测值，所以有(4)3o; = 0.840,=±0.9mm二、随机向量函数向量的方差阵（约15分钟）设随机向量X、Y，其自协方差阵分别是Dxx、Dy，互协方差阵是Dxy，又设有mXX1函数向量U=AX+A。，V=BY+B。，其中A、A、B、B。是常系数矩阵。则有xmtxrxIrxmmxIDuu = E[AU(AU)"]= AE(AXAY)A" = ADxxA

而               = 2 2 2 1 2 2 1 2 2 1 1 2 1 n n n n n x x x x x x x x x x x x x x x DXX                 当自变量 ( , , , ) 1 2 n x x  x 相互独立时，有               = 2 2 2 0 0 0 0 0 0 2 1 n x x x DXX           此时 = = = n i i x T z XX i KD K k 1 2 2 2   【例题 1】在 1:500 的地图上，量得某两点间的距离是 d = 23.4mm， d 的量距误差是  d = 0.2mm 。求两点间的实地距离 S 和其精度  S 。 解： S = 500d = 50023.4 =11700mm =11.7m  S = 500 d = 500(0.2) = 100mm = 0.1m 最后写成 S =11.7m 0.1m 【例题 2】设 x 是独立观测值 L1、 L2 和 L3 的函数，即： 1 2 3 7 4 7 2 7 1 x = L + L + L 已知 L1、 L2 和 L3 的中误差是 1 = 3mm、 2 = 2mm 和  3 = 1mm ，求函数 x 的精度。 解：因为 L1、 L2 和 L3 是独立观测值，所以有 0.84 7 4 7 2 7 1 2 3 2 2 2 2 2 1 2 2  =       +       +       x =     x = 0.9mm 二、随机向量函数向量的方差阵 设随机向量 n1 X 、m1 Y ，其自协方差阵分别是 DXX 、DYY ，互协方差阵是 DXY ，又设有 函数向量 1 0 1 1     = + t t t n n U A X A ， 1 0 1 1     = + r r r m m V B Y B ，其中 A 、 A0 、 B 、 B0 是常系数矩阵。则有   T XX T T T t t DUU = E U U = AE XX A = AD A  ( ) ( ) ： （约 10 分钟） （约 15 分钟）

Dw = EAV(AW)"]- BE(AYAY")BT = BDB"Duv = E[AU(AV)"]= AE(AXAYT)B = ADxBDvu =E[AV(AU)’)= BE(AYAYT)A" = BD A" =(Duv)三、随机向量函数是非线性的情况（约20分钟）1、设有观测值向量X的非线性函数z=F(X)=F(xi,x2x,），且随机向量X的方差阵是Dxx，求随机函数z的方差？。对非线性函数进行全微分有()()af)dx +dx, +dz.dx,,1-1,2,(ax2)0(axn)o(ax,)。令OT(ox,)(ox2ox则dZ=KdX,D=KDxKT。课堂教学小结：1. 方差、协方差阵;2.单个线性面数的方差的传播3.多个线性品数方差的传播。4.非线性西数方差的传据

  T YY T T T r r DVV = E V V = BE YY B = BD B  ( ) ( )   T XY T T T t r DUV = E U V = AE XY B = AD B  ( ) ( )   T UV T YX T T T r t DVU = E V(U) = BE(YX )A = BD A = (D )  三、随机向量函数是非线性的情况 1、设有观测值向量 n1 X 的非线性函数 ( ) ( , , ) 1 2 n z = f X = f x x x ，且随机向量 n1 X 的方 差阵是 DXX ，求随机函数 z 的方差 2  z 。 对非线性函数进行全微分有 n n i i i i dx x f dx x f dx x f dz 0 2 2 0 1 1 0           + +           +           =  ，i =1,2, t 令               = t z z z Z  2 1 ，                                                                                                                 =  1 0 2 0 0 0 2 2 0 2 1 0 2 0 1 2 0 1 1 0 1 n t t t n n t n x f x f x f x f x f x f x f x f x f K        则 dZ = KdX ， T DZZ = KDXXK 。 （约 20 分钟） ） 课堂教学小结： 1. 方差、协方差阵； 2.单个线性函数的方差的传播； 3.多个线性函数方差的传播。 4.非线性函数方差的传播