《线性代数》课程PPT教学课件（同济第五版）第1章 行列式 1.6 行列式按行（列）展开

行列式 第六节 行列式按行（列）展开 余子式与代数余子式 行列式按行（列）展开法则 三、小结思考题 带助式 四了

、余子式与代数余子式 例如 41142413 421 22 423 011422433+01242331+01342132 431 32 433 -凸1123032-凸1202133-413022031， =a11(a2033-023432+a2(a23431-421433） +413(a21432-02031） 22 a21 一w2 23 21 23 33 l33 33

1 1 2 3 3 2 1 2 2 1 3 3 1 3 2 2 3 1, 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 a a a a a a a a a a a a a a a a a a − − − = + + 31 32 33 21 22 23 11 12 13 a a a a a a a a a 例如 ( ) = a11 a22a33 − a23a32 ( ) + a12 a23a31 − a21a33 ( ) + a13 a21a32 − a22a31 3 1 3 3 2 1 2 3 1 3 3 1 3 3 2 1 2 3 1 2 3 2 3 3 2 2 2 3 1 1 a a a a a a a a a a a a a a = a − + 一、余子式与代数余子式

在n阶行列式中，把元素au所在的第i行和第j 列划去后，留下来的n一1阶行列式叫做元素a 的余子式，记作M· 记 A,=（+M,叫做元素a的代数余子式. 例如 L12 3 4 11 L12 14 D M23= 31 32 l34 L31 L32 L34 a41 L42 L44 L41 L42 L44 423=(-1)2+3M23=-M23

在 阶行列式中，把元素 所在的第 行和第 列划去后，留下来的 阶行列式叫做元素 的余子式，记作 n aij i j n −1 aij M . ij 记 ( ) ij， i j Aij M + = − 1 叫做元素 aij 的代数余子式． 例如 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 a a a a a a a a a a a a a a a a D = 41 42 44 31 32 34 11 12 14 23 a a a a a a a a a M = ( ) 23 2 3 A23 1 M + = − . = −M23

041-.店2.134t D- l21 2 L23 24 21 L23 424 31 32 33 (34 M12=a31 433 343 02.a4gtr 41 043 L44 A2=（-1)2M2=-M2 11 12413 M44=021 22 a23,A4=(-1)H4M44=M4 31L32L33 行列式的每个元素分别对应着一个余子式和一 个代数余子式

, 41 42 43 44 31 32 33 34 21 22 23 24 11 12 13 14 a a a a a a a a a a a a a a a a D = , 41 43 44 31 33 34 21 23 24 12 a a a a a a a a a M = ( ) 12 1 2 A12 1 M + = − . = −M12 , 31 32 33 21 22 23 11 12 13 44 a a a a a a a a a M = ( 1) . 44 44 4 4 A44 = − M = M + 个代数余子式. 行列式的每个元素分别对应着一个余子式和一

引理 一个n阶行列式，如果其中第i行所有 元素除外都为零，那末这行列式等于，与它的 代数余子式的乘积， 即D=A 11 L12 L13 14 例如 D- 21 L22 L23 24 0 0 L33 0 L41 042 43 QAA 11 12 14 =(-1)3+a3 21 l22 L24 L41 42 L44 区回

引理 一个 阶行列式，如果其中第 行所有 元素除 外都为零，那末这行列式等于 与它的 代数余子式的乘积，即 D = aijA．ij n i ij a ij a 41 42 43 44 33 21 22 23 24 11 12 13 14 0 0 0 a a a a a a a a a a a a a D = ( 1) . 41 42 44 21 22 24 11 12 14 33 3 3 a a a a a a a a a a + = − 例如

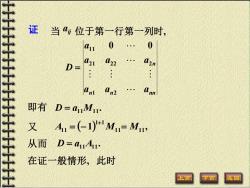
证 当位于第一行第一列时， 11 0 0 D= L21 L22 Anl 02. 即有 D=a11M11 又 A,=(-1)M1=M 从而 D=a11A11 在证一般情形，此时 上页

证 当 ij 位于第一行第一列时, a n n nn n a a a a a a a D       1 2 21 22 2 11 0 0 = 即有 . D = a11M11 又 ( ) 11 1 1 A11 1 M + = − , = M11 从而 . D = a11A11 在证一般情形, 此时

411 j D= 0 0 0 把D的第行依次与第i-1行，第i-2行，第1行对调， 0 新 0 .: 得D=(-1)-a-i . Wi-1,j -1,n : 可 区回

n nj nn ij j n a a a a a a a D             1 11 1 1 = 0 0 把D的第i行依次与第i −1行,第i − 2行,第1行对调, 得 ( ) n nj nn i i j i n ij i a a a a a a a D             1 1,1 1, 1, 1 0 0 1 − − − − = − ij a ij a

再把D的第列依次与第j-1列，第j-2列，第1列 对调， 得 By 0 0 .: D=(1(-1a-0 An:j-I 上页

, 1 , 2 , 1 对调 再把D的第j列依次与第j − 列 第j − 列 第 列 得 ( ) ( ) nj n j nn i j i j i n ij i j a a a a a a a D             , 1 1, 1, 1 1, 1 1 0 0 1 1 − − − − − − − = −  − ij a

0 0 .: =(←1-3a- L-1,j-1 Qi-1.n .: l L ,j-1 j 0 0 =(1a- Qi-1,n L可 On,j-1 Ann 区回

( ) nj n j nn i j i j i n ij i j a a a a a a a             , 1 1, 1, 1 1, 2 0 0 1 − − − − − + − = − ( ) nj n j nn i j i j i n ij i j a a a a a a a             , 1 1, 1, 1 1, 0 0 1 − − − − − + = − ij a ij a

0 0 元素a在行列式a-, . ai- . i-1 中的 . An,j-1 ·· 余子式仍然是a在 411 j n .: : D= 0 y . 0 中的余子式M : Qnl Ann 上页

n nj nn ij j n a a a a a a a D             1 11 1 1 = 0 0 中的余子式 . Mij 余子式仍然是 在 元素 在行列式 中的 ij nj n j nn i j i j i n ij ij a a a a a a a a a             , 1 1, 1, 1 1, 0 0 − − − − − ij a ij a