《线性代数》课程PPT教学课件（同济第五版）第4章 向量组的线性相关性 4.1 n维向量

向量组的孩恨相关烟 第一节n维向量 n维向量的概念 n维向量的表示方法 三 向量空间 四、小结思考题 返

一、n维向量的概念 定义1n个有次序的数a1,a2,an所组成的数 组称为n维向量，这n个数称为该向量的1个分量， 第i个数a,称为第个分量. 分量全为实数的向量称为实向量， 分量全为复数的向量称为复向量， 上页 返回

定义1 . , , , 1 2 第 个 数 称为第 个分量 组称为 维向量，这 个数称为该向量的 个分量， 个有次序的数 所组成的数 i a i n n n n a a a i  n 分量全为复数的向量称为复向量. 分量全为实数的向量称为实向量， 一、 n 维向量的概念

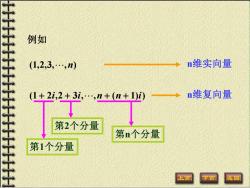
例如 (1,2,3,.,n） n维实向量 (1+2i,2+3i,.,n+(n+1)→n维复向量 第2个分量 第n个分量 第1个分量 上页

例如 (1,2,3,  ,n) (1 + 2i,2 + 3i,  ,n + (n + 1)i) n维实向量 n维复向量 第1个分量 第n个分量 第2个分量

二、n维向量的表示方法 n维向量写成一行，称为行向量，也就是行 矩阵， 通常用a,b,a,B等表示， 如： a'=(a1,a2,.,n) n维向量写成一列，称为列向量，也就是列 矩阵，通常用4，b,a,B等表示，如： L= 上页 区回

( , , , ) 1 2 n T a = a a  a               = an a a a  2 1 二、 维向量的表示方法 维向量写成一行，称为行向量，也就是行 矩阵，通常用   等表示，如： T T T T a ,b , , n 维向量写成一列，称为列向量，也就是列 矩阵，通常用 a,b,, 等表示，如： n n

注意 1.行向量和列向量总被看作是两个不同的 向量； 2.行向量和列向量都按照矩阵的运算法则 进行运算； 3.当没有明确说明是行向量还是列向量时， 都当作列向量. 上页

注意 １．行向量和列向量总被看作是两个不同的 向量； ２．行向量和列向量都按照矩阵的运算法则 进行运算； ３．当没有明确说明是行向量还是列向量时， 都当作列向量

三、向量空间 向 解析几何 (n≤3) 线性代数 坐 既有大小又有方向的量 有次序的实数组成的数组 标 几何形象：可随意 代数形象：向量的 平行移动的有向线段 坐标表 示式 aT=(a1,2,an) 回

向 量 解析几何 (n  3) 线性代数 既有大小又有方向的量 有次序的实数组成的数组 几何形象： 可随意 平行移动的有向线段 代数形象： 向量的 坐 标 表 示 式 ( , , , ) 1 2 n T a = a a  a 坐 标 系 三、向量空间

空 间 解析几何 (n≤3) 线性代数 点空间：点的集合 向量空间：向量的集合 标 几何形象： 空间 代数形象： 向量空 直线、曲线、空间 间中的 平 面 平面或曲面 (x,y,z)ax+by+cz=d} r=(x,y,z)ax+by+cz=dj P(x,y,z) 对应 r=(x,⑦) 上页

空 间 (n  3) 解析几何 线性代数 点空间：点的集合 向量空间：向量的集合 坐 标 系 代数形象： 向量空 间 中 的 平 面 r x y z ax by cz d T =( , , ) + + = 几何形象： 空间 直线、曲线、空间 平面或曲面 (x, y,z)ax+by+cz=d P(x, y,z) r (x, y,z) T = 一 一 对 应

n>3时，n维向量没有直观的几何形象. R={c=(xx2,x)xx2,x.eR} 叫做n维向量空间. ==x)aa:++ax=b 叫做n维向量空间R”中的n-I维超平面. 上页 回

R x x x xn x x xn R n T = =( 1 , 2 ,  , ) 1 , 2 ,  ,  x x x xn a x a x an xn b T  = =( 1 , 2 ,  , ) 1 1+ 2 2++ = 叫做 n 维向量空间． n  3 时， n 维向量没有直观的几何形象． 叫做 维向量空间 R 中的 维超平面． n n n − 1

n维向量的实际意义 确定飞机的状态，需 要以下6个参数： 机身的仰角 2 机翼的转角 机身的水平转角 (0≤0<2π) 飞机重心在空间的位置参数P(x,y,☑ 所以，确定飞机的状态，需用6维向量 a=(x,y,3,p,w,8) 上页

确定飞机的状态，需 要以下6个参数： 飞机重心在空间的位置参数P(x,y,z) 机身的水平转角  (0    2 ) 机身的仰角 ) 2 2 (     −   机翼的转角  (−    ) 所以，确定飞机的状态，需用6维向量 a = (x, y,z,, , ) n 维向量的实际意义

课堂讨论 在日常工作、学习和生活中，有许多问题都 需要用向量来进行描述，请同学们举例说明. 上页 这回

课堂讨论 在日常工作、学习和生活中，有许多问题都 需要用向量来进行描述，请同学们举例说明．