《数学建模与数学实验》课程试题库

第1题足球队排名次 属性：综合评价模型：1993年全国数学建模竞赛题 下表给出了我国12支足球队在1988-1989年全国足球级联赛中的成绩，要求 1)设计一个依据这些成绩排出诸队名次的算法，并给出用该算法排名次的结果。 2)把算法推广到任意N个队的情况。 3)讨论：数据应具备什么样的条件，用你的方法才能够排出诸队的名次 对下表的说明： 1)12支球队依次记作T1.T2.,T12 2)符号X表示两队未曾比赛。 3)数字表示两队比赛结果，如3行与8列交叉处的数字表示：T3与T8比赛了2场：T3与T8的进 球之比为0：1和3：1. 第2题锁具装箱 属性：整数规划模型：1994年全国数学建模竞赛题 某厂生产一种弹子锁具，每个锁具的钥匙有5个槽，每个槽的高度从1,2,3,4,5,6}6个数（单 位略)中任取一数.由于工艺及其它原因，制造锁具时对5个槽的高度还有两个限制：至少有3个不 同的数：相邻两槽高度之差不能为5.满足以上条件制造出来的所有互不相同的锁具称为一批.出来的所 有互不相同的锁具称为一批。 从项客的利 自然希望在每批锁具中“一把钥匙开一把锁”但是在当前工艺条件下，对于同 批中两个锁具是否能够互开，有以下试验结果：若二者相对应的5个槽的高度中有4个相同，另 的高度差关 传可能互开 下可能互开，原米， 锁具中随意地取每6 实儿箱到几十箱，他们跑怨购得的锁具会出现互相开的情形现鸭羽雨 为顾正 1 同装多少箱 "为售都提货种方案包活如何装箱（仍是60个锁具一箱，如何给箱子以标志，出售时如 何利用这些标志，使团体顾客不再或减少抱怨 3》采取你提出的方案，团体顾客的购买量不超过多少箱，就可以保证一定不会出现互 4)按照原来的装箱办法，如何定量地衡量团体顾客抱怨互开的程度（试对购买一、二箱者给出具 体结果). 第3题最优捕鱼策略 属性：微分方程模型：1996年全国数学建模竟赛题 为了保护人类赖以生存的自然环境，可再生资源（如渔业、林业资源）的开发必须适度。一种合理、 简化的策略是，在实现可持续收获的前提下，追求最大产量或最佳效益。 考虑对某种鱼（鲳鱼）的最优捕捞策略： 假设这种鱼分4个年给组，称】给鱼，4龄角。冬年龄组每条角的平均重量分别 5.07,11.55,17.86,22.99(克)：各年龄组鱼的自然死亡率均为0.8(1/年 为 节性集中 立卵 繁殖，平均每条4龄鱼的产卵量为1.109×10（个）：3龄鱼的产卵量为这个数的一半，2龄鱼和1龄鱼 不产卵，产卵和孵化期为每年的最后4个月：卵孵化并成活为1龄鱼，成活率(1龄鱼条数与产卵总是 之比)为1.22×10"/(1.22×10"+n). 渔业管理部门规定，盘年只允许在产：卵卵化期前的8个月内进行捕捞作业。如果每年投入的捕捞能力 (如渔船数、下网次数等)固定不变，这时单位时间捕捞量将与各年龄组鱼群条数成正比。比例系数不妨

第 1 题 足球队排名次 属性：综合评价模型；1993 年全国数学建模竞赛题 下表给出了我国 12 支足球队在 1988-1989 年全国足球级联赛中的成绩，要求 1）设计一个依据这些成绩排出诸队名次的算法，并给出用该算法排名次的结果。 2）把算法推广到任意 N 个队的情况。 3）讨论：数据应具备什么样的条件，用你的方法才能够排出诸队的名次。 对下表的说明： 1）12 支球队依次记作 T1,T2,.，T12. 2）符号 X 表示两队未曾比赛。 3）数字表示两队比赛结果，如 T3 行与 Y8 列交叉处的数字表示：T3 与 T8 比赛了 2 场；T3 与 T8 的进 球之比为 0：1 和 3：1。 第 2 题 锁具装箱 属性：整数规划模型；1994 年全国数学建模竞赛题 某厂生产一种弹子锁具, 每个锁具的钥匙有 5 个槽, 每个槽的高度从 {1,2,3,4, 5,6} 6 个数 (单 位略) 中任取一数. 由于工艺及其它原因, 制造锁具时对 5 个槽的高度还有两个限制: 至少有 3 个不 同的数; 相邻两槽高度之差不能为 5. 满足以上条件制造出来的所有互不相同的锁具称为一批.出来的所 有互不相同的锁具称为一批. 从顾客的利益出发, 自然希望在每批锁具中"一把钥匙开一把锁". 但是在当前工 艺条件下, 对于同 一批中两个锁具是否能够互开, 有以下试验结果: 若二者相对应的 5 个 槽的高度中有 4 个相同, 另一个 的高度差为 1, 则可能互开; 在其它情形下, 不可能互开.原来, 销售部门在一批锁具中随意地取每 60 个装一箱出售. 团体顾客往往购买几箱到几十箱, 他们抱怨购得的锁具会出现互相开的情形. 现聘聘请 你为顾问, 回答并解 决以下问题: 1) 每一批锁具有多少个, 装多少箱. 2) 为销售部门提供一种方案, 包括如何装箱(仍是 60 个锁具一箱),如何给箱子以标志, 出售时如 何利用这些标志, 使团体顾客不再或减少抱怨. 3) 采取你提出的方案, 团体顾客的购买量不超过多少箱, 就可以保证一定不会出现互 4) 按照原来的装箱办法, 如何定量地衡量团体顾客抱怨互开的程度 (试对购买一、二 箱者给出具 体结果). 第 3 题 最优捕鱼策略 属性：微分方程模型；1996 年全国数学建模竞赛题 为了保护人类赖以生存的自然环境，可再生资源（如渔业、林业资源）的开发必须适度。一种合理、 简化的策略是，在实现可持续收获的前提下，追求最大产量或最佳效益。 考虑对某种鱼（鲳鱼）的最优捕捞策略： 假设这种鱼分４个年龄组：称１龄鱼，.，４龄鱼。各年龄组每条鱼的平均重量分别为 5.07,11.55,17.86,22.99（克）；各年龄组鱼的自然死亡率均为 0.8（１/年）；这种鱼为季节性集中产卵 繁殖，平均每条４龄鱼的产卵量为 1.109×105 (个）；３龄鱼的产卵量为这个数的一半，２龄鱼和１龄鱼 不产卵，产卵和孵化期为每年的最后４个月；卵孵化并成活为１龄鱼，成活率（１龄鱼条数与产卵总是 n 之比）为 1.22×1011/(1.22×1011+n). 渔业管理部门规定，每年只允许在产卵卵化期前的８个月内进行捕捞作业。如果每年投入的捕捞能力 （如渔船数、下网次数等）固定不变，这时单位时间捕捞量将与各年龄组鱼群条数成正比。比例系数不妨

称捕捞强度系数。通常使用13m网眼的拉网，这种网只能捕捞3龄鱼和4龄鱼，其两个捕捞强度系数之 比为0.42：1。渔业上称这种方式为固定努力量捕捞。 1)建立数学模型分析如何可持续捕获（即每年开始捕捞时渔场中各年龄组鱼群不变），并且在此前 提下得到最高的年收获量（捕捞总重量） 2)某渔业公司承包这种鱼的捕捞业务5年，合同要求鱼群的生产能力不能受到太大的破坏。已知承 包时各年龄组鱼群的数量分别为：122,29.7,10.1,3.29(×10条)，如果仍用固定努力量的捕捞方式，该 公司采取怎样的策略才能使总收获量最高。 第4题节水洗衣机 属性：统计模型：1996年全国数学建横竟赛题 我国淡水资源有限，节约用水人人有责。洗衣机在家庭用水中占有相当大的份额，目前洗衣机已非常 普 节约洗农机用 水十分重要。假设在放入衣物和洗涤剂后洗农机的运行过程为：加水-漂水-脱水 -漂水-脱水-一加水-漂水-脱水（称“加水-漂水-脱水”为运行一轮）。请为洗衣机设计一种程序（包 括运行多少轮、每轮加多少水等)，使得在满足一定洗涤效果的条件下，总用水量最少。选用合理的数据 进行计算。对照目前常用的洗衣机的运行情况，对你的模型和结果作出评价。 第5题截断切割 属性：整数规划模型：1997年全国数学建模竞赛题 某些工业部门（如贵重石材加工等）采用截断切制的加工方式。这里“截断切割”是指将物体沿某个 切割平面分成两部分。从一个长方体中加工出一个己知尺寸、位置预定的长方体（这两个长方体的对应表 面是平行的)，通常要经过6次截断切割。 设水平切割单位面积的费用是垂直切割单位面积费用的r倍，且当先后两次垂直切割的平面（不管它 红之何香穿插水行时因调泰可列具表题外费用要求 一 次序（称 的方法，使加工费用最少 先指定的)，详细要求如下： 1)需考虑的不同切割方式的总数。 2)给出上述问题的数学模型和求解方法。 3)试对某部门用的如下准则作出评价：每次选择一个加工费用最少的待切割面进行切制 4)对 0的情形有无简明的优化 准则 5)用以下实例验证你的方法：待加工长方体和成品长方体的长、宽、高分别为10、14.5、 19和3 2、4,二者左侧面、正面、底面之间的距离分别为6、7、9（单位均为厘米）。垂直切割费用为每平方厘 米1元，r和e的数据有以下4组： a.r=l,e=0:b.r.5,e0 =8.e=0 dr=1.5:2<=e<15. 对最后组数据应给出所有最优解，并进行讨论

称捕捞强度系数。通常使用１３mm 网眼的拉网，这种网只能捕捞３龄鱼和４龄鱼，其两个捕捞强度系数之 比为 0.42:1。渔业上称这种方式为固定努力量捕捞。 １）建立数学模型分析如何可持续捕获（即每年开始捕捞时渔场中各年龄组鱼群不变），并且在此前 提下得到最高的年收获量（捕捞总重量）。 ２）某渔业公司承包这种鱼的捕捞业务５年，合同要求鱼群的生产能力不能受到太大的破坏。已知承 包时各年龄组鱼群的数量分别为：122,29.7,10.1,3.29(×109 条），如果仍用固定努力量的捕捞方式，该 公司采取怎样的策略才能使总收获量最高。 第 4 题 节水洗衣机 属性：统计模型；1996 年全国数学建模竞赛题 我国淡水资源有限，节约用水人人有责。洗衣机在家庭用水中占有相当大的份额，目前洗衣机已非常 普及，节约洗衣机用水十分重要。假设在放入衣物和洗涤剂后洗衣机的运行过程为：加水-漂水-脱水-加 水-漂水-脱水-.-加水-漂水-脱水（称“加水-漂水-脱水”为运行一轮）。请为洗衣机设计一种程序（包 括运行多少轮、每轮加多少水等），使得在满足一定洗涤效果的条件下，总用水量最少。选用合理的数据 进行计算。对照目前常用的洗衣机的运行情况，对你的模型和结果作出评价。 第 5 题 截断切割 属性：整数规划模型；1997 年全国数学建模竞赛题 某些工业部门（如贵重石材加工等）采用截断切割的加工方式。这里“截断切割”是指将物体沿某个 切割平面分成两部分。从一个长方体中加工出一个已知尺寸、位置预定的长方体（这两个长方体的对应表 面是平行的），通常要经过 6 次截断切割。 设水平切割单位面积的费用是垂直切割单位面积费用的 r 倍，且当先后两次垂直切割的平面(不管它 们之间是否穿插水平切割)不平行时，因调整刀具需额外费用 e。 试为这些部门设计一种安排各面加工 次序（称“切割方式”）的方法，使加工费用最少。（由工艺要求，与水平工作台接触的长方体底面是事 先指定的），详细要求如下： 1）需考虑的不同切割方式的总数。 2）给出上述问题的数学模型和求解方法。 3）试对某部门用的如下准则作出评价：每次选择一个加工费用最少的待切割面进行切割。 4）对于 e = 0 的情形有无简明的优化准则。 5）用以下实例验证你的方法：待加工长方体和成品长方体的长、宽、高分别为 10、14.5、 19 和 3、 2、4，二者左侧面、正面、底面之间的距离分别为 6、7、9（单位均为厘米）。垂直切割费用为每平方厘 米 1 元，r 和 e 的数据有以下 4 组： a. r =1, e = 0; b. r =1.5, e =0; c. r =8, e =0; d. r =1.5; 2 <= e <= 15. 对最后一组数据应给出所有最优解，并进行讨论

第6题投资的收益和风险 属性：优化模型：1998年全国数学建模竞赛题 市场上有n种资产（如股票、债券、）Si(1=1,n)供投资者选择，某公司有数额为M的一笔相 当大的资金可用作一个时期的投资。公司财务分析人员对这种资产进行了评估，估算出在这一时期内购 买S1的平均收益率为，并预测出购买S1的风险损失率为。考虑到投资越分散，总的风险越小，公司 确定，当用这笔资金购买若干种资产时，总体风险可用所投资的S1中最大的一个风险来度量】 购买S1要付交易费，费率为，并且当购买额不超过给定值时，交易费按购买“计算（不买当然 无须付费)。另外，假定同期银行存款利率是，且既无交易费又无风险。（口=5%）己知n=4时的相关 数据如下： Si 5() 9() P() 4(元) S1 2.5 1 103 S2 3 1.5 198 S3 5.5 4.5 心 S4 25 2.6 6.5 40 试给该公司设计一种投资组合方案，即用给定的资金M,有选择地购买若干种资产或存银行生息 使净收益尽可能大，而总体风险尽可能小。 试就一般情况对以上问题进行讨论，并利用以下数据进行计算 Si 店偶) 4:(偶) P:(% (元 9.6 42 2.1 S2 18.5 54 3.2 407 S3 49.4 6.0 428 S4 23.9 42 1.5 549 S5 8.1 1.2 7.6 270 39 3.4 397

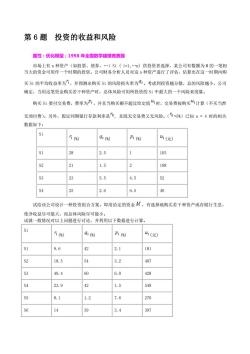
第 6 题 投资的收益和风险 属性：优化模型；1998 年全国数学建模竞赛题 市场上有 n 种资产（如股票、债券、.）Si ( i=1,.n) 供投资者选择，某公司有数额为 M 的一笔相 当大的资金可用作一个时期的投资。公司财务分析人员对这 n 种资产进行了评估，估算出在这一时期内购 买 Si 的平均收益率为 ，并预测出购买 Si 的风险损失率为 。考虑到投资越分散，总的风险越小，公司 确定，当用这笔资金购买若干种资产时，总体风险可用所投资的 Si 中最大的一个风险来度量。 购买 Si 要付交易费，费率为 ，并且当购买额不超过给定值 时，交易费按购买 计算（不买当然 无须付费）。另外，假定同期银行存款利率是 , 且既无交易费又无风险。（ =5%）已知 n = 4 时的相关 数据如下： Si (%) (%) (%) (元) S1 28 2.5 1 103 S2 21 1.5 2 198 S3 23 5.5 4.5 52 S4 25 2.6 6.5 40 试给该公司设计一种投资组合方案，即用给定的资金 ，有选择地购买若干种资产或存银行生息， 使净收益尽可能大，而总体风险尽可能小。 试就一般情况对以上问题进行讨论，并利用以下数据进行计算。 Si (%) (%) (%) (元) S1 9.6 42 2.1 181 S2 18.5 54 3.2 407 S3 49.4 60 6.0 428 S4 23.9 42 1.5 549 S5 8.1 1.2 7.6 270 S6 14 39 3.4 397

S7 40.7 68 5.6 178 31.2 33.4 3.1 220 33.6 53.3 2.7 475 S10 36.8 40 29 248 511 11.8 31 5.1 195 S12 9 5.5 5.7 320 S13 35 46 2.7 267 S14 9.4 63 4.5 328 S15 15 23 7.6 131 第7题灾情巡视路线 属性：网络优化模型：1998年全国数学建模竟赛题 下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。 今年夏天该县遗受水灾。为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、 村巡视。巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。 1、若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。 2、假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间1小时，汽车行驶速度V=35 公里/小时 要在24小时内完成巡视。 至少应分几组： 给出这种分组下你认为最佳的巡视路线。 3、在上述关于T，t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少：给出在这 种最短时间完成巡视的要求下，你认为最佳的巡视路线。 4、若巡视组数己定（如三组），要求尽快完成巡视，讨论T,t和V改变对最佳巡视路线的影响。 第8题中国人口增长预测 属性：微分方程模型：2007年全国数学建模竞赛题 中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。根据已有数据，运用数学建模 的方法，对中国人口做出分析和预测是一个重要问题。 近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以 及乡村人口城镇化等因素，这些都影响若中国人口的增长。2007年初发布的《国家人口发展战略研究报告》 (附录1)还做出了进一步的分析 关于中国人口问恩已有多方面的研究，并积累了大量数据资料。附录2就是从《中国人口统计年鉴 上收集到的部分数据

S7 40.7 68 5.6 178 S8 31.2 33.4 3.1 220 S9 33.6 53.3 2.7 475 S10 36.8 40 2.9 248 S11 11.8 31 5.1 195 S12 9 5.5 5.7 320 S13 35 46 2.7 267 S14 9.4 5.3 4.5 328 S15 15 23 7.6 131 第 7 题 灾情巡视路线 属性：网络优化模型；1998 年全国数学建模竞赛题 下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。 今年夏天该县遭受水灾。为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、 村巡视。巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。 1、 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。 2、 假定巡视人员在各乡（镇）停留时间 T=2 小时，在各村停留时间 t=1 小时，汽车行驶速度 V=35 公里/小时。要在 24 小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。 3、 在上述关于 T , t 和 V 的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这 种最短时间完成巡视的要求下，你认为最佳的巡视路线。 4、 若巡视组数已定(如三组），要求尽快完成巡视，讨论 T，t 和 V 改变对最佳巡视路线的影响。 第 8 题 中国人口增长预测 属性：微分方程模型；2007 年全国数学建模竞赛题 中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。根据已有数据，运用数学建模 的方法，对中国人口做出分析和预测是一个重要问题。 近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以 及乡村人口城镇化等因素，这些都影响着中国人口的增长。2007 年初发布的《国家人口发展战略研究报告》 (附录 1) 还做出了进一步的分析。 关于中国人口问题已有多方面的研究，并积累了大量数据资料。附录 2 就是从《中国人口统计年鉴》 上收集到的部分数据

试从中国的实际情况和人口增长的上述特点出发，参考附录2中的相关数据（也可以搜索相关文献和 补充新的数据)，建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测 特别要指出你们模型中的优点与不足之处 附录1《国家人口发展战略研究报告》 附录2人口数据(《中国人口统计年鉴》中的部分数据)及其说明 第9题乘公交，看奥运 属性：图论或优化模型；2007年全国数学建模竟赛题 届时有大量观众到现场观看奥运比赛 、地铁等)出行 这些来。城市的公系 有了很大发展，北京市的公交线路己达800条以上，使得公众的出行更加通畅、便利，但同时也面临多条 线路的选择问题。针对市场需求，某公司准备研制开发一个解决公交线路选择问题的自主查询计算机系统。 为了设计这样一个系统，其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的 各种不同需求。请你们解决如下问题： 1、考虑公 线路，给出任意两公汽站点之间线路选择问题的一般数学模型与算法。并根据附录数 据，利用你们的模 可算法，求出以下6对起始站一终到站之间的最佳路线（要有清晰的评价说明）。 ④、S0008323 018 *5048 2 同时考虑公汽与地铁线路，解决以上问题」 假设又知道所有站点之间的步行时间，请你给出任意两站点之间线路选择问题的数学模型。 【附录1】基本参数设定 相邻公汽站平均行驶时间（包括停站时间）：3分钟 相邻地铁站平均行驶时间（包括停站时间）：2.5分钟 公汽换乘公汽平均耗时： 5分钟（其中步行时间2分钟） 地铁换乘地铁平均耗时： 4分钟（其中步行时间2分钟） 地铁快果公汽平均耗时： 7分钟（其中步行时间4分钾 公气 地用 耗 价与分段计价两种，标记于线路后：其中分段计价的票价为：0~20站：1元： (无论地铁线路何是否换乘) 注：以上参数均为简化向题而作的假设，未必与实际数据完全吻合 【附录2】公交线路及相关信息（见数据文件B2007data.rar) 第10题手机“套餐”优惠几何 属性：综合评价模型：2007年全国数学建模竟赛题 手机现已成为人们日常工作、社交、经营等社会活动中必备的工具之一，近年来通信业务量飞速增长 (见附件1)。 手机资费间题一直是人们关心的热点间题，多少年来资费方案始终没有实质性变化。但是2007年1 月以来上海、北京、广东等地的移动和联通两大运营商都相继推出了“手机单向收费方案”一各种品牌 的“套餐”，手机“套餐”的花样琳琅满目，让人眼花缭乱。人们不禁要问：手机“套餐”究竞优惠几何？

试从中国的实际情况和人口增长的上述特点出发，参考附录 2 中的相关数据（也可以搜索相关文献和 补充新的数据），建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测； 特别要指出你们模型中的优点与不足之处。 附录 1 《国家人口发展战略研究报告》 附录 2 人口数据（《中国人口统计年鉴》中的部分数据）及其说明 第 9 题 乘公交，看奥运 属性：图论或优化模型；2007 年全国数学建模竞赛题 我国人民翘首企盼的第 29 届奥运会明年 8 月将在北京举行，届时有大量观众到现场观看奥运比赛， 其中大部分人将会乘坐公共交通工具（简称公交，包括公汽、地铁等）出行。这些年来，城市的公交系统 有了很大发展，北京市的公交线路已达 800 条以上，使得公众的出行更加通畅、便利，但同时也面临多条 线路的选择问题。针对市场需求，某公司准备研制开发一个解决公交线路选择问题的自主查询计算机系统。 为了设计这样一个系统，其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的 各种不同需求。请你们解决如下问题： 1、仅考虑公汽线路，给出任意两公汽站点之间线路选择问题的一般数学模型与算法。并根据附录数 据，利用你们的模型与算法，求出以下 6 对起始站→终到站之间的最佳路线（要有清晰的评价说明）。 (1)、S3359→S1828 (2)、S1557→S0481 (3)、S0971→S0485 (4)、S0008→S0073 (5)、S0148→S0485 (6)、S0087→S3676 2、同时考虑公汽与地铁线路，解决以上问题。 3、假设又知道所有站点之间的步行时间，请你给出任意两站点之间线路选择问题的数学模型。 【附录 1】基本参数设定 相邻公汽站平均行驶时间(包括停站时间)： 3 分钟 相邻地铁站平均行驶时间(包括停站时间)： 2.5 分钟 公汽换乘公汽平均耗时： 5 分钟(其中步行时间 2 分钟) 地铁换乘地铁平均耗时： 4 分钟(其中步行时间 2 分钟) 地铁换乘公汽平均耗时： 7 分钟(其中步行时间 4 分钟) 公汽换乘地铁平均耗时： 6 分钟(其中步行时间 4 分钟) 公汽票价：分为单一票价与分段计价两种，标记于线路后；其中分段计价的票价为：0～20 站：1 元； 21～40 站：2 元；40 站以上：3 元 地铁票价：3 元（无论地铁线路间是否换乘） 注：以上参数均为简化问题而作的假设，未必与实际数据完全吻合。 【附录 2】公交线路及相关信息 （见数据文件 B2007data.rar） 第 10 题 手机“套餐”优惠几何 属性：综合评价模型；2007 年全国数学建模竞赛题 手机现已成为人们日常工作、社交、经营等社会活动中必备的工具之一，近年来通信业务量飞速增长 (见附件 1) 。 手机资费问题一直是人们关心的热点问题， 多少年来资费方案始终没有实质性变化。但是 2007 年 1 月以来上海、北京、广东等地的移动和联通两大运营商都相继推出了“手机单向收费方案”-各种品牌 的“套餐”，手机“套餐”的花样琳琅满目，让人眼花缭乱。人们不禁要问：手机“套餐”究竟优惠几何？

请参照中国移动公司现行的资费标准和北京的全球通“畅听99套餐”、上海的“全球通3套餐”方 案（见附件2），建立数学模型分析研究下列问题： (1)给出北京、上海各“套餐”方案的资费计算方法，并针对不同（通话量）需求的用户，分析说明 各种“套餐”方案适应于什么样的用户？ (②)提出你们对各种资费方案的评价准则和方法，据此对北京、上海推出的“套餐”方案与现行的资 费标准作分析、比较，并给出评价。 (3)北京移动公司2007年5月公日又推出了所谓的全球通“被叫全免费计划”方案，即月租50元， 本地被叫免费，其他项目资费均同现行的资费标准，还要求用户至少在网一年。你们又如何评价这个方案？ 并说明理由。 (④)如果移动公司聘请你们帮助设计一个全球通手机的资费方案，你们会考虑哪些因素？根据你们 的研究结果和北京、上海的实际情况，在较现有“套餐”方案运营商的收入降低不超过10%的条件下，用数 学建模方法设计一个你们认为合理的“套餐”方案。 附件12006年中国通信业的统计资料 附件2中国移动手机的资费方案 第11题出版社的资源配置 属性：多层优化模型；2006年全国数学建模竟赛题 出版社的资源主要包括人力资源、生产资源、资金和管理资源等，它们都捆绑在书号上，经过各个部 门的运作，形成成本（策划成本、编辑成本、生产成本、库存成本、销售成本、财务与管理成本等）和利 润。 某个以教材类出版物为主的出版社，总社领导每年需要针对分社提交的生产计划申请书、人力资源情 况以及市场信息分析，将总量一定的书号数合理地分配给各个分补，使出版的数材产生最好的经济效益。 般以增加强势产品支持力 宝实上。电于各个尖进提交的蛋魂书号益量木牙共的丝骨划分根据分配到的罗政量，再重 度的原则优化资源配置。资源配置完成后 对学科所属每个课程作出出版计划，付诸实施。 资源配置是总社每年进行的重要决策，直接关系到出版社的当年经济效益和长远发展战略。由于市场 信息（主要是需求与竞争力）通常是不完全的，企业自身的数据收集和积累也不足，这种情况下的决策问 题在我国企业中是普遍存在的。 题附录中给出 该出版社所掌握的 一些数据资料，请你们根据这些数据资料，利用数学建模的方法 在信息不足的条件下，提出以量化分析为基础的资源（书号）配置方法，给出一个明确的分配方案，向出 版社提供有益的建议。 [附录] 附件1：问卷调杏表： 附件2：问卷调查数据（五年）： 附件3：各课程计划及实际销售数据表(5年)： 附件4：各课程计划申请或实际获得的书号数列表(6年)： 附件5：9个分社人力资原细目

请参照中国移动公司现行的资费标准和北京的全球通“畅听 99 套餐”、上海的“全球通 68 套餐”方 案（见附件 2），建立数学模型分析研究下列问题： (1) 给出北京、上海各“套餐”方案的资费计算方法，并针对不同（通话量）需求的用户，分析说明 各种“套餐”方案适应于什么样的用户？ (2) 提出你们对各种资费方案的评价准则和方法, 据此对北京、上海推出的“套餐”方案与现行的资 费标准作分析、比较，并给出评价。 (3) 北京移动公司 2007 年 5 月 23 日又推出了所谓的全球通“被叫全免费计划”方案，即月租 50 元， 本地被叫免费，其他项目资费均同现行的资费标准，还要求用户至少在网一年。你们又如何评价这个方案？ 并说明理由。 (4) 如果移动公司聘请你们帮助设计一个全球通手机的资费方案, 你们会考虑哪些因素? 根据你们 的研究结果和北京、上海的实际情况，在较现有“套餐”方案运营商的收入降低不超过 10%的条件下,用数 学建模方法设计一个你们认为合理的“套餐”方案。 附件 1 2006 年中国通信业的统计资料 附件 2 中国移动手机的资费方案 第 11 题 出版社的资源配置 属性：多层优化模型；2006 年全国数学建模竞赛题 出版社的资源主要包括人力资源、生产资源、资金和管理资源等，它们都捆绑在书号上，经过各个部 门的运作，形成成本（策划成本、编辑成本、生产成本、库存成本、销售成本、财务与管理成本等）和利 润。 某个以教材类出版物为主的出版社，总社领导每年需要针对分社提交的生产计划申请书、人力资源情 况以及市场信息分析，将总量一定的书号数合理地分配给各个分社，使出版的教材产生最好的经济效益。 事实上，由于各个分社提交的需求书号总量远大于总社的书号总量，因此总社一般以增加强势产品支持力 度的原则优化资源配置。资源配置完成后，各个分社（分社以学科划分）根据分配到的书号数量，再重新 对学科所属每个课程作出出版计划，付诸实施。 资源配置是总社每年进行的重要决策，直接关系到出版社的当年经济效益和长远发展战略。由于市场 信息（主要是需求与竞争力）通常是不完全的，企业自身的数据收集和积累也不足，这种情况下的决策问 题在我国企业中是普遍存在的。 本题附录中给出了该出版社所掌握的一些数据资料，请你们根据这些数据资料，利用数学建模的方法， 在信息不足的条件下，提出以量化分析为基础的资源（书号）配置方法，给出一个明确的分配方案，向出 版社提供有益的建议。 [附录] 附件 1：问卷调查表； 附件 2：问卷调查数据（五年）； 附件 3：各课程计划及实际销售数据表（5 年）； 附件 4：各课程计划申请或实际获得的书号数列表（6 年）； 附件 5：9 个分社人力资源细目

第12题艾滋病疗法的评价及疗效的预测 属性：统计和优化模型；2006年全国数学建模竞赛题 艾滋病是当前人类社会最严重的瘟疫之一，从1981年发现以来的20多年间，它已经吞噬了近3000 万人的生命。 艾滋病的医学全名为“获得性免疫缺损综合症”，英文简称AIDS,它是由艾滋病毒（医学全名为“人体免 疫缺损病毒”，英文简称V)引起的。这种病毒破坏人的免疫系统，使人体丧失抵抗各种疾病的能力 从而严重危害人的生命。人类免疫系统的CD4细胞在抵御V的入侵中起着重要作用，当CD4被V感染 而裂解时，其数量会急剧减少，HV将迅速增加，导致AIDS发作。 艾滋病治疗的目的，是尽量减少人体内HIV的数量，同时产生更多的CD4,至少要有效地降低C①4减 少的速度，以提高人体免疫能力。 迄今为止人类还没有找到能根治AIDS的疗法，目前的一些AIS疗法不仅对人体有副作用，而且成本也很 高。许多国家和医疗组织都在积极试验、寻找更好的AIS疗法。 现在得到了美国艾滋病医疗试验机构ACTG公布的两组数据。 ACTG320(见附件I)是同时服用zidovudin: (齐多夫定)，lamivudine(拉美夫定)和indinavir(茚地那韦)3种药物的300多名病人每隔几周测 的CD4和HV的浓度（每毫升血液里的数量）。193A(见附件2)是将1300多名病人随机地分为4组，每 组按下述4种疗法中的一种服药，大约每隔8周测试的CD4浓度（这组数据缺HV浓度，它的测试成本很 高。4种疗法的日用药分别为：60或400 didanosine(去羟基苷 ,这两种药按月轮换 使用：600 ngzidovudine加2.25 ngzalcitabine(扎西他滨)：600 gzidovudine加400 mg didanosine: 600 mg zidovudine加400 mg didanosine,再加400 mg nevirapine(奈韦拉平)。 请你完成以下问题： (1)利用附件1的数据，预测继续治疗的效果，或者确定最佳治疗终止时间（继续治疗指在测试终止 后继续服药，如果认为继续服药效果不好，则可选择提前终止治疗)。 (2)利用附件2的 评价4种疗法的优劣（仅以CD4为标准），并对较优的疗法预测继续治疗的 效果，或者确定最佳治疗终止时间。 (3)艾滋病药品的主要供给商对不发达国家提供的药品价格如下：600 mg zidovudine1.60美元，400mg didanosine0.85美元，2.25 mg zalcitabine1.85关元，400 mg nevirapine1.20美元。如果病人需要 考虑4种疗法的费用，对(2)中的评价和预测（或者提前终止）有什么改变。 第13题易拉罐形状和尺寸的最优设计 属性：优化模型：2006年全国数学建模竞赛题 我们只要稍加留意就会发现销量很大的饮料（例如饮料量为355毫升的可口可乐、青岛啤酒等）的饮 料罐（即易拉罐）的形状和尺寸几乎都是一样的。看来，这并非偶然，这应该是某种意义下的最优设计。当 然，对于单个的易拉罐来说，这种最优设计可以节省的钱可能是很有限的，但是如果是生产几亿，甚至几 十亿个易拉罐的话，可以节约的钱就很可观了 现在就请你们小组来 状和尺寸的最优设计问题。具体说，请你们完成以下的 1.取一个饮料量为355毫升的易拉罐，例如355毫升的可口可乐饮料罐，测量你们认为验证模型所需要 的数据，例如易拉罐各部分的直径、高度，厚度等，并把数据列表加以说明： 如果数据不是 你们自己测量得到的，那么你们必须注明出处。 2.设易拉罐是一个正圆柱体。什么是它的最优设计？其结果是否可以合理地说明你们所测量的易拉罐的

第 12 题 艾滋病疗法的评价及疗效的预测 属性：统计和优化模型；2006 年全国数学建模竞赛题 艾滋病是当前人类社会最严重的瘟疫之一，从 1981 年发现以来的 20 多年间，它已经吞噬了近 3000 万人的生命。 艾滋病的医学全名为“获得性免疫缺损综合症”，英文简称 AIDS，它是由艾滋病毒（医学全名为“人体免 疫缺损病毒”, 英文简称 HIV）引起的。这种病毒破坏人的免疫系统，使人体丧失抵抗各种疾病的能力， 从而严重危害人的生命。人类免疫系统的 CD4 细胞在抵御 HIV 的入侵中起着重要作用，当 CD4 被 HIV 感染 而裂解时，其数量会急剧减少，HIV 将迅速增加，导致 AIDS 发作。 艾滋病治疗的目的，是尽量减少人体内 HIV 的数量，同时产生更多的 CD4，至少要有效地降低 CD4 减 少的速度，以提高人体免疫能力。 迄今为止人类还没有找到能根治 AIDS 的疗法，目前的一些 AIDS 疗法不仅对人体有副作用，而且成本也很 高。许多国家和医疗组织都在积极试验、寻找更好的 AIDS 疗法。 现在得到了美国艾滋病医疗试验机构 ACTG 公布的两组数据。 ACTG320（见附件 1）是同时服用 zidovudine （齐多夫定），lamivudine（拉美夫定）和 indinavir（茚地那韦）3 种药物的 300 多名病人每隔几周测试 的 CD4 和 HIV 的浓度（每毫升血液里的数量）。193A（见附件 2）是将 1300 多名病人随机地分为 4 组，每 组按下述 4 种疗法中的一种服药，大约每隔 8 周测试的 CD4 浓度（这组数据缺 HIV 浓度，它的测试成本很 高）。4 种疗法的日用药分别为：600mg zidovudine 或 400mg didanosine（去羟基苷），这两种药按月轮换 使用；600 mg zidovudine 加 2.25 mg zalcitabine（扎西他滨）；600 mg zidovudine 加 400 mg didanosine； 600 mg zidovudine 加 400 mg didanosine，再加 400 mg nevirapine（奈韦拉平）。 请你完成以下问题： （1）利用附件 1 的数据，预测继续治疗的效果，或者确定最佳治疗终止时间（继续治疗指在测试终止 后继续服药，如果认为继续服药效果不好，则可选择提前终止治疗）。 （2）利用附件 2 的数据，评价 4 种疗法的优劣（仅以 CD4 为标准），并对较优的疗法预测继续治疗的 效果，或者确定最佳治疗终止时间。 (3) 艾滋病药品的主要供给商对不发达国家提供的药品价格如下：600mg zidovudine 1.60 美元，400mg didanosine 0.85 美元，2.25 mg zalcitabine 1.85 美元，400 mg nevirapine 1.20 美元。如果病人需要 考虑 4 种疗法的费用，对（2）中的评价和预测（或者提前终止）有什么改变。 第 13 题 易拉罐形状和尺寸的最优设计 属性：优化模型；2006 年全国数学建模竞赛题 我们只要稍加留意就会发现销量很大的饮料 (例如饮料量为 355 毫升的可口可乐、青岛啤酒等) 的饮 料罐(即易拉罐)的形状和尺寸几乎都是一样的。看来，这并非偶然，这应该是某种意义下的最优设计。当 然，对于单个的易拉罐来说，这种最优设计可以节省的钱可能是很有限的，但是如果是生产几亿，甚至几 十亿个易拉罐的话，可以节约的钱就很可观了。 现在就请你们小组来研究易拉罐的形状和尺寸的最优设计问题。具体说，请你们完成以下的任务： 1． 取一个饮料量为 355 毫升的易拉罐，例如 355 毫升的可口可乐饮料罐，测量你们认为验证模型所需要 的数据，例如易拉罐各部分的直径、高度，厚度等，并把数据列表加以说明； 如果数据不是 你们自己测量得到的，那么你们必须注明出处。 2． 设易拉罐是一个正圆柱体。什么是它的最优设计？其结果是否可以合理地说明你们所测量的易拉罐的

形状和尺寸，例如说，半径和高之比，等等。 3.设易拉罐的中心纵断面如下图所示，即上面部分是一个正圆台，下面部分是一个正圆柱体 什么是它的最优设计？其结果是否可以合理地说明你们所测量的易拉罐的形状和尺寸。 4.利用你们对所测量的易拉罐的洞察和想象力，做出你们自己的关于易拉罐形状和尺寸的最优设计。 用你们做本题以及以前学习和实践数学建模的亲身体验，写一篇短文（不超过1000字，你们的论文中 必须包括这篇短文)，阐述什么是数学建模、 它的关键步骤，以及难点。 第14题煤矿瓦斯和煤尘的监测与控制 属性：统计模型：2006年全国数学建模竟赛题 煤和安全生产是我国目前亟待解决的问题之一，做好井下瓦斯和煤尘的监测与控制是实现安全生产的 关键环节（见附件1）。 瓦断是一种无毒、无色、无味的可燃气体，其主要成分是甲烷，在矿井中它通常从煤岩裂缝中通出」 瓦斯爆炸需要三个条件：空气中瓦斯达到一定的浓度：足够的氧气： 一定温度的火源！ 煤尘是在煤炭开采过程中产生的可燃性粉尘。煤尘爆炸必须具备三个条件：煤尘本身具有爆炸性：煤 尘悬浮于空气中并达到一定的浓度：存在引爆的高温热源。试验表明，一般情况下煤尘的燥炸浓度是30~ 2000g/,而当矿井空气中瓦斯浓度增加时，会使煤尘爆炸下限降低，结果如附表1所示。 国家《煤矿安全规程》给出了煤矿预防瓦斯爆炸的措施和操作规程，以及相应的专业标准（见附件2）。 规程要求煤矿必须安装完善的通风系统和瓦斯自动监控系统，所有的采煤工作面、掘进面和回风巷都要安 装甲烷传感器，每个传感器都与地面控制中心相连，当井下瓦斯浓度超标时，控制中心将自动切断电源 停止采煤作业 人员撤 采煤现场。具体内容见附件2的第 章和第三章 附图1是有两个采煤工作面和一个掘进工作面的矿井通风系统示意图，请你结合附表2的监测数据， 按照煤矿开采的实际情况研究下列问题： (1)根据《煤矿安全规程》第一百三十三条的分类标准（见附件2），鉴别该矿是属于“低瓦斯矿井”还 是“高瓦斯矿井”。 (2)根据《煤矿安全规程》第一百六十八条的规定，并参照附表1，判断该煤矿不安全的程度（即发生爆 炸事故的可能性)有多大： (3)为了保障安全生产，利用两个可控风门调节各采煤工作面的风量，通过一个局部通风机和风筒实项 掘进巷的通风（见下面的注）。根据附图1所示各井巷风量的分流情况、对各井巷中风速的要求（见《煤 矿安全规程》第一百零一条)，以及瓦斯和煤尘等因素的影响，确定该煤矿所需要的最佳（总）通风量， 以及两个采煤工作面所需要的风量和局部通风机的额定风量（实际中，井巷可能会 出现漏风现象) 注掘进巷需要安装局部 通风机 其欲定风型 般为150400/min。局部通风机所在的巷道中至少 需要有15%的余裕风量（新鲜风）才能保证风在巷道中的正常流动，否则可能会出现负压导致乏风逆流， 即局部通风机将乏风吸入并送至掘进工作面。 名词解释

形状和尺寸，例如说，半径和高之比，等等。 3． 设易拉罐的中心纵断面如下图所示，即上面部分是一个正圆台，下面部分是一个正圆柱体。 什么是它的最优设计？其结果是否可以合理地说明你们所测量的易拉罐的形状和尺寸。 4． 利用你们对所测量的易拉罐的洞察和想象力，做出你们自己的关于易拉罐形状和尺寸的最优设计。 用你们做本题以及以前学习和实践数学建模的亲身体验，写一篇短文(不超过 1000 字，你们的论文中 必须包括这篇短文)，阐述什么是数学建模、它的关键步骤，以及难点。 第 14 题 煤矿瓦斯和煤尘的监测与控制 属性：统计模型；2006 年全国数学建模竞赛题 煤矿安全生产是我国目前亟待解决的问题之一，做好井下瓦斯和煤尘的监测与控制是实现安全生产的 关键环节（见附件 1）。 瓦斯是一种无毒、无色、无味的可燃气体，其主要成分是甲烷，在矿井中它通常从煤岩裂缝中涌出。 瓦斯爆炸需要三个条件：空气中瓦斯达到一定的浓度；足够的氧气；一定温度的引火源。 煤尘是在煤炭开采过程中产生的可燃性粉尘。煤尘爆炸必须具备三个条件:煤尘本身具有爆炸性；煤 尘悬浮于空气中并达到一定的浓度；存在引爆的高温热源。试验表明，一般情况下煤尘的爆炸浓度是 30～ 2000g/m3，而当矿井空气中瓦斯浓度增加时，会使煤尘爆炸下限降低，结果如附表 1 所示。 国家《煤矿安全规程》给出了煤矿预防瓦斯爆炸的措施和操作规程，以及相应的专业标准 (见附件 2)。 规程要求煤矿必须安装完善的通风系统和瓦斯自动监控系统，所有的采煤工作面、掘进面和回风巷都要安 装甲烷传感器，每个传感器都与地面控制中心相连，当井下瓦斯浓度超标时，控制中心将自动切断电源， 停止采煤作业，人员撤离采煤现场。具体内容见附件 2 的第二章和第三章。 附图 1 是有两个采煤工作面和一个掘进工作面的矿井通风系统示意图，请你结合附表 2 的监测数据， 按照煤矿开采的实际情况研究下列问题： （1）根据《煤矿安全规程》第一百三十三条的分类标准 (见附件 2)，鉴别该矿是属于“低瓦斯矿井”还 是“高瓦斯矿井”。 （2）根据《煤矿安全规程》第一百六十八条的规定，并参照附表 1，判断该煤矿不安全的程度（即发生爆 炸事故的可能性）有多大？ （3）为了保障安全生产，利用两个可控风门调节各采煤工作面的风量，通过一个局部通风机和风筒实现 掘进巷的通风（见下面的注）。根据附图 1 所示各井巷风量的分流情况、对各井巷中风速的要求（见《煤 矿安全规程》第一百零一条），以及瓦斯和煤尘等因素的影响，确定该煤矿所需要的最佳（总）通风量， 以及两个采煤工作面所需要的风量和局部通风机的额定风量（实际中，井巷可能会出现漏风现象）。 注 掘进巷需要安装局部通风机，其额定风量一般为 150~400 m3 /min。局部通风机所在的巷道中至少 需要有 15%的余裕风量（新鲜风）才能保证风在巷道中的正常流动，否则可能会出现负压导致乏风逆流， 即局部通风机将乏风吸入并送至掘进工作面。 名词解释

(1)采煤工作面：矿井中进行开采的煤壁（采煤现场）。 (2)掘进巷：用爆破或机械等方法开凿出的地下巷道，用以准备新的采煤区和采煤工作面， (3)掘进工作面：掘进巷尽头的开掘现场 (4)新鲜风：不含瓦斯和煤尘等有害物质的风流。 (5)乏风：含有一定浓度的瓦撕和煤尘等有害物质的风流。 第15题长江水质的评价和预测 属性：统计和综合评价模型：2005年全国数学建模竟赛题 水是人类赖以生存的资源，保护水资源就是保护我们自己，对于我国大江大河水资源的保护和治理应 是重中之重。专家们呼吁：“以人为本，建设文明和谐社会，改善人与自然的环境，减少污染。 长江是我国第一、世界第三大河流，长江水质的污染程度日趋严重，已引起了相关政府部门和专家们 的高度重视。2004年10月，由全国政协与中国发展研究院联合组成“保护长江万里行”考察团，从长江 上游宜宾到下游上海。对沿线21个重占城市做了实地考察，揭示了一幅长江污垫的直实画面。其污染程 度让人触目 。为此，专家们提出“若不及时拯救，长江生态10年内将濒临崩溃”（附件1），并发出 “拿什么拯救癌变长江”的呼唤（附件2）。 附件3给出了长江沿线17个观测站（地区）近两年多主要水质指标的检测数据，以及干流上7个观 测站近一年多的基本数据（站点距离、水流量和水流速）。通常认为一个观测站（地区）的水质污染主要 来自于本地区的排污和上游 污水 一般说来，江河自身对污染物都有一定的自然净化能力，即污染物在 水环境中通过物理降解、化学降解和生物降解等使水中污染物的浓度降低。反映江河自然净化能力的指标 称为降解系数。事实上，长江干流的自然净化能力可以认为是近似均匀的，根据检测可知，主要污染物高 锰酸盐指数和氨氨的降解系数通常介于0.10.5之间，比如可以考虑取0.2（单位：1/天）。附件4是 “1995^2004年长江流域水质报告”给出的主要统计数据。下面的附表是国标(GB3838-2002)给出的《地 表水环境质量标准》中4个主要项目标准限值，其中、Ⅲ类为可饮用水。 请你们研究下列问题： (1)对长江近两年多的水质情况做出定量的综合评价，并分析各地风水质的污染状况。 (2)研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪些地区？ (3)假如不采取更有效的治理措施，依照过去10年的主要统计数据，对长江未来水质污染的发展差 势做出预测分析，比如研究未来10年的情况。 (4)根据你的预测分析，如果未来10年内每年都要求长江干流的V类和V类水的比例控制在20%以 内，且没有劣V类水，那么每年需要处理多少污水？ (5)你对解决长江水质污染问题有什么切实可行的建议和意见。 第16题DVD在线租赁 属性：离散优化模型：2005年全国数学建模竟赛题 随者信息时代的到来，网络成为人们生活中越来越不可或缺的元素之一。许多网站利用其强大的资源 和知名度，面向其会员群提供日益专业化和便捷化的服务。例如，音像制品的在线租赁就是一种可行的服 务。这项服务充分发挥了网络的诸多优势，包括传播范围广泛、直达核心消费群、强烈的互动性、感官性 强、成本相对低廉等，为顾客提供更为周到的服务

（1）采煤工作面：矿井中进行开采的煤壁 (采煤现场)。 （2）掘进巷：用爆破或机械等方法开凿出的地下巷道，用以准备新的采煤区和采煤工作面。 （3）掘进工作面：掘进巷尽头的开掘现场。 （4）新鲜风：不含瓦斯和煤尘等有害物质的风流。 （5）乏风：含有一定浓度的瓦斯和煤尘等有害物质的风流。 第 15 题 长江水质的评价和预测 属性：统计和综合评价模型；2005 年全国数学建模竞赛题 水是人类赖以生存的资源，保护水资源就是保护我们自己，对于我国大江大河水资源的保护和治理应 是重中之重。专家们呼吁：“以人为本，建设文明和谐社会，改善人与自然的环境，减少污染。” 长江是我国第一、世界第三大河流，长江水质的污染程度日趋严重，已引起了相关政府部门和专家们 的高度重视。2004 年 10 月，由全国政协与中国发展研究院联合组成“保护长江万里行”考察团，从长江 上游宜宾到下游上海，对沿线 21 个重点城市做了实地考察，揭示了一幅长江污染的真实画面，其污染程 度让人触目惊心。为此，专家们提出“若不及时拯救，长江生态 10 年内将濒临崩溃”（附件１），并发出 了“拿什么拯救癌变长江”的呼唤（附件 2）。 附件 3 给出了长江沿线 17 个观测站（地区）近两年多主要水质指标的检测数据，以及干流上７个观 测站近一年多的基本数据（站点距离、水流量和水流速）。通常认为一个观测站（地区）的水质污染主要 来自于本地区的排污和上游的污水。一般说来，江河自身对污染物都有一定的自然净化能力，即污染物在 水环境中通过物理降解、化学降解和生物降解等使水中污染物的浓度降低。反映江河自然净化能力的指标 称为降解系数。事实上，长江干流的自然净化能力可以认为是近似均匀的，根据检测可知，主要污染物高 锰酸盐指数和氨氮的降解系数通常介于 0.1~0.5 之间，比如可以考虑取 0.2 (单位：1/天)。附件 4 是 “1995~2004 年长江流域水质报告”给出的主要统计数据。下面的附表是国标(GB3838-2002) 给出的《地 表水环境质量标准》中 4 个主要项目标准限值，其中Ⅰ、Ⅱ、Ⅲ类为可饮用水。 请你们研究下列问题： （1）对长江近两年多的水质情况做出定量的综合评价，并分析各地区水质的污染状况。 （2）研究、分析长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在哪些地区? （3）假如不采取更有效的治理措施，依照过去 10 年的主要统计数据，对长江未来水质污染的发展趋 势做出预测分析，比如研究未来 10 年的情况。 （4）根据你的预测分析，如果未来 10 年内每年都要求长江干流的Ⅳ类和Ⅴ类水的比例控制在 20%以 内，且没有劣Ⅴ类水,那么每年需要处理多少污水？ （5）你对解决长江水质污染问题有什么切实可行的建议和意见。 第 16 题 DVD 在线租赁 属性：离散优化模型；2005 年全国数学建模竞赛题 随着信息时代的到来，网络成为人们生活中越来越不可或缺的元素之一。许多网站利用其强大的资源 和知名度，面向其会员群提供日益专业化和便捷化的服务。例如，音像制品的在线租赁就是一种可行的服 务。这项服务充分发挥了网络的诸多优势，包括传播范围广泛、直达核心消费群、强烈的互动性、感官性 强、成本相对低廉等，为顾客提供更为周到的服务

考虑如下的在线DVD租赁问题。顾客缴纳一定数量的月费成为会员，订购DD租赁服务。会员对哪些 WD右兴趣，只要在线提交打单，网站封会通时快第的方式尽能墙足要求。合员提交的打单句括多张DWD 这些DD是基于其偏爱程度排序的。网站会根据手头现有的DD数量和会员的订单进行分 每个会员每 个月租赁次数不得超过2次，每次获得3张DD。会员看完3张DD之后，只需要将DM放进网站提供的 信封里寄回（邮费由网站承担），就可以继续下次租质。请考虑以下问题： 1)网站正准备购买一些新的DVD,通过问卷调查100个会员，得到了愿意观看这些DD的人数（表1给 出了其中5种DVD的数据)。此外，历中数据显示，60%的会员每月租质DWD两次，而另外的40%只租 次。假设网站现有10万个会员，对表1中的每种D D来说，应该至少准备多 张，才能保证希望石 个月内能够看到该DD?如果要求保证在三个月内至少95%的会员能够 2)表2中列出了网站手上100种DWD的现有张数和当前需要处理的1000位会员的在线订单（表2的数据 格式示例如下表2，具体数据请从http://mcm.edu.cn/mcm05/problems2005c.ap下载)，如何对这些 DD进行分配，才能使会员获得最大的满意度？请具体列出前30位会员（即C0001C0030)分别获得 此 3)继续考虑表2，并假设表2中DD的现有数量全部为0。如果你是网站经营管理人员，你如何决定每种 DVD的购买量，以及如何对这些DD进行分配，才能使一个月内95%的会员得到他想看的DVD,并且满 意度吊大？ 4)如果你是网站经营管理人员，你觉得在DD的需求预测、购买和分配中还有那些重要间颗值得研究？ 请明确提出你的问题，并尝试建立相应的数学模型。 表1对1000个会员调查的部分结果 DWD名称 DVDI DVD2 I DVD3 DVD4 DVD5 愿意观看的人数200 100 50 95 10 表2现有DWD张数和当前需要处理的会员的在线订单（表格格式示例） DVD编号 D001 D002 D003 D004 DVD现右数量 10 40 15 20 C000 会员 C0002 0 0 0 0 在发 C0003 0 0 0 订单 C0004 0 0 注：D001D100表示100种DWD,C0001℃1000表示1000个会员，会员的在线订单用数字1,2，.表示，数 字越小表示会员的偏爱程度越高，数字0表示对应的DD当前不在会员的在线订单中。 第17题雨量预报方法的评价 属性：统计和综合评价模型：2005年全国数学建模竟赛题 雨量预报对农业生产和城市工作和生活有重要作用，但准确、及时地对雨量作出预报是一个十分困难 的问题，广受世界各国关注。我国某地气象台和气象研究所正在研究6小时雨量预报方法，即每天晚上20 点预报从21点开始的4个时段(21点至次日3点，次日3点至9点，9点至15点，15点至21点)在某 些位置的雨量，这些位置位于东经120度、北纬32度附近的53×47的等距网格点上。同时设立91个观

考虑如下的在线 DVD 租赁问题。顾客缴纳一定数量的月费成为会员，订购 DVD 租赁服务。会员对哪些 DVD 有兴趣，只要在线提交订单，网站就会通过快递的方式尽可能满足要求。会员提交的订单包括多张 DVD， 这些 DVD 是基于其偏爱程度排序的。网站会根据手头现有的 DVD 数量和会员的订单进行分发。每个会员每 个月租赁次数不得超过 2 次，每次获得 3 张 DVD。会员看完 3 张 DVD 之后，只需要将 DVD 放进网站提供的 信封里寄回（邮费由网站承担），就可以继续下次租赁。请考虑以下问题： 1） 网站正准备购买一些新的 DVD，通过问卷调查 1000 个会员，得到了愿意观看这些 DVD 的人数（表 1 给 出了其中 5 种 DVD 的数据）。此外，历史数据显示，60%的会员每月租赁 DVD 两次，而另外的 40%只租 一次。假设网站现有 10 万个会员，对表 1 中的每种 DVD 来说，应该至少准备多少张，才能保证希望看 到该 DVD 的会员中至少 50%在一个月内能够看到该 DVD？如果要求保证在三个月内至少 95%的会员能够 看到该 DVD 呢？ 2） 表 2 中列出了网站手上 100 种 DVD 的现有张数和当前需要处理的 1000 位会员的在线订单（表 2 的数据 格式示例如下表 2，具体数据请从 http://mcm.edu.cn/mcm05/problems2005c.asp 下载），如何对这些 DVD 进行分配，才能使会员获得最大的满意度？请具体列出前 30 位会员（即 C0001~C0030）分别获得 哪些 DVD。 3） 继续考虑表 2，并假设表 2 中 DVD 的现有数量全部为 0。如果你是网站经营管理人员，你如何决定每种 DVD 的购买量，以及如何对这些 DVD 进行分配，才能使一个月内 95%的会员得到他想看的 DVD，并且满 意度最大？ 4） 如果你是网站经营管理人员，你觉得在 DVD 的需求预测、购买和分配中还有哪些重要问题值得研究？ 请明确提出你的问题，并尝试建立相应的数学模型。 表 1 对 1000 个会员调查的部分结果 DVD 名称 DVD1 DVD2 DVD3 DVD4 DVD5 愿意观看的人数 200 100 50 25 10 表 2 现有 DVD 张数和当前需要处理的会员的在线订单（表格格式示例） DVD 编号 D001 D002 D003 D004 . DVD 现有数量 10 40 15 20 . 会员 在线 订单 C0001 6 0 0 0 . C0002 0 0 0 0 . C0003 0 0 0 3 . C0004 0 0 0 0 . . . . . . . 注：D001~D100 表示 100 种 DVD, C0001~C1000 表示 1000 个会员, 会员的在线订单用数字 1,2,.表示，数 字越小表示会员的偏爱程度越高，数字 0 表示对应的 DVD 当前不在会员的在线订单中。 第 17 题 雨量预报方法的评价 属性：统计和综合评价模型；2005 年全国数学建模竞赛题 雨量预报对农业生产和城市工作和生活有重要作用，但准确、及时地对雨量作出预报是一个十分困难 的问题，广受世界各国关注。我国某地气象台和气象研究所正在研究 6 小时雨量预报方法，即每天晚上 20 点预报从 21 点开始的 4 个时段（21 点至次日 3 点，次日 3 点至 9 点，9 点至 15 点，15 点至 21 点）在某 些位置的雨量，这些位置位于东经 120 度、北纬 32 度附近的 53×47 的等距网格点上。同时设立 91 个观