《数学建模与数学实验》教学教学资源（案例）鸭子过河

化学工业出版社 数学建模及典型案例分析

化学工业出版社

鸭子过河 ●有只鸭子想游到河对岸的某个位置O,如果它的方向 始终朝着目标O。求这只鸭子的游动曲线

鸭子过河  有只鸭子想游到河对岸的某个位置O，如果它的方向 始终朝着目标O。求这只鸭子的游动曲线

示例1鸭子过河 ·模型假设 1.假设河的两岸为平行直线，河宽为： 2.鸭子游水的速率为b,水流速率为α，均为常数： 3初始时鸭子的位置为A; 4.鸭子游动的方向始终指向O

示例1 鸭子过河  模型假设 1.假设河的两岸为平行直线，河宽为h; 2.鸭子游水的速率为b, 水流速率为a, 均为常数; 3.初始时鸭子的位置为A; 4.鸭子游动的方向始终指向O

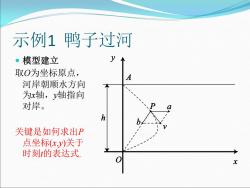
示例1鸭子过河 ·模型建立 取O为坐标原点， A 河岸朝顺水方向 为x轴，y轴指向 对岸。 h 关键是如何求出P 点坐标(x,y)关于 时刻的表达式：

示例1 鸭子过河  模型建立 取O为坐标原点， 河岸朝顺水方向 为x轴，y轴指向 对岸。 关键是如何求出P 点坐标(x,y)关于 时刻t的表达式

示例1鸭子过河 时刻鸭子本身的速度为 6=b OP b 河水速度为a=(a,0),所以合速度为 bx v=a+b=(a- by

示例1 鸭子过河 t时刻鸭子本身的速度为 河水速度为 所以合速度为 ),( || 22 yx yx b OPOP bb     aa ),0,(  ( , ), 22 22 yx by yx bx abav       

示例1鸭子过河 即 dx bx =a- di (1.1) dy by dt Vx2+y2 又由初始条件有 x(0)=0,y(0)=h (1.2 (1.1)12)就是所求问题的一个微分方程模型

示例1 鸭子过河 即 又由初始条件有 (1.1)(1.2) 就是所求问题的一个微分方程模型。   hyx .)0(,0)0( (1.2)       , d d , d d 22 22 yx by t y yx bx a t x (1.1)

示例1鸭子过河 ·模型求解 1数值解 设时间步长为△t则 P=(xo,y)=(0,h)v=(a,-b) “ bxi (1.3) P=(x,y)=P-1+v△t,i=1,2

示例 1 鸭子过河  模型求解 1.数值解 设时间步长为Δt, 则                     ),( ,2,1, ( , ), ),(),0(),( 11 2 1 2 1 1 2 1 2 1 1 1 000 0 itvPyxP yx by yx bx av bavhyxP iiiii ii i ii i i (1.3)

示例1鸭子过河 当y<0时，说明鸭子已经到达河对岸，应停止计算 由(1.3)可以算出t,时刻鸭子的位置的近似值

示例1 鸭子过河 当yi <0时, 说明鸭子已经到达河对岸，应停止计算. 由(1.3)可以算出ti时刻鸭子的位置的近似值

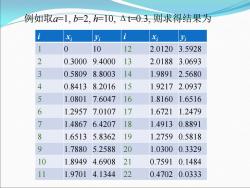
例如取a=1,b=2,h=10,个t=0.3,则求得结果为 Yi 1 0 10 12 2.0120 3.5928 2 0.30009.4000 13 2.0188 3.0693 3 0.5809 8.8003 14 1.9891 2.5680 4 0.8413 8.2016 15 1.9217 2.0937 5 1.0801 7.6047 16 1.8160 1.6516 6 1.29577.0107 17 1.6721 1.2479 1.4867 6.4207 18 1.4913 0.8891 8 1.65135.8362 19 1.27590.5818 1.7880 5.2588 20 1.0300 0.3329 10 1.8949 4.6908 21 0.7591 0.1484 11 1.9701 4.1344 22 0.47020.0333

i xi yi i xi yi 1 0 10 12 2.0120 3.5928 2 0.3000 9.4000 13 2.0188 3.0693 3 0.5809 8.8003 14 1.9891 2.5680 4 0.8413 8.2016 15 1.9217 2.0937 5 1.0801 7.6047 16 1.8160 1.6516 6 1.2957 7.0107 17 1.6721 1.2479 7 1.4867 6.4207 18 1.4913 0.8891 8 1.6513 5.8362 19 1.2759 0.5818 9 1.7880 5.2588 20 1.0300 0.3329 10 1.8949 4.6908 21 0.7591 0.1484 11 1.9701 4.1344 22 0.4702 0.0333 例如取a=1, b=2, h=10, Δt=0.3, 则求得结果为

计算(1.3)的Matlab代码 c1cg清屏 鸭子过河问题 a=1;b=2;h=10;dt=0.3;%设置参数 i=1; P=[0,h]；号初始值 while P(i,2)>0 i=i+1; v=[a-b.*P(i-1,1)./sqrt(P(i-1,1).^2+P(i-1,2).^2), -b.*P(i-1,2)./sqrt(P(i-1,1).^2+P(i-1,2).^2)]；号计算第i步的速度 P(i,:)=P(i-1,:)+v.*dt;号计算第i步位置 end P各显示结果 p1ot(P(:,1),P(:,2))8作图

计算(1.3)的Matlab代码 clc %清屏 % 鸭子过河问题 a=1; b=2; h=10; dt=0.3; %设置参数 i=1; P=[0,h]; %初始值 while P(i,2)>0 i=i+1; v=[a - b.*P(i-1,1)./sqrt(P(i-1,1).^2+P(i-1,2).^2), -b.*P(i-1,2)./sqrt(P(i-1,1).^2+P(i-1,2).^2)]; %计算第i步的速度 P(i,:)= P(i-1,:)+ v.*dt; %计算第i步位置 end P %显示结果 plot(P(:,1),P(:,2)) %作图