《数学建模与数学实验》教学教学资源（PPT课件）第8讲 最短路问题

数学建模与数学实验 最短路问题

数学建模与数学实验 最短路问题

实验目的 1.了解最短路的算法及其应用 2.会用MATLAB软件求最短路 实验内容 L.图论的基本概念 2.最短路问题及其算法 3.最短路的应用 4.建模案例：最优截断切割问题 《实验作业

实验目的 实验内容 2．会用MATLAB软件求最短路 1．了解最短路的算法及其应用 1．图 论 的 基 本 概 念 2．最 短 路 问 题 及 其 算 法 3．最 短 路 的 应 用 4．建模案例：最优截断切割问题 5．实验作业

图论的基本概念 一、图的概念 1.图的定义 2.顶点的次数 3.子图 二、图的矩阵表示 1.关联矩阵 2.邻接矩阵 返回

图 论 的 基 本 概 念 一、 图 的 概 念 1．图的定义 2．顶点的次数 3．子图 二、 图 的 矩 阵 表 示 1． 关联矩阵 2． 邻接矩阵 返回

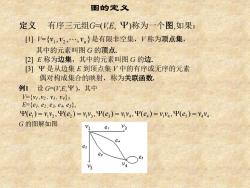
图的定义 定义有序三元组G=(E,Ψ)称为一个图，如果： [小={y1,2,.,yn}是有限非空集，V称为顶点集， 其中的元素叫图G的顶点 [2]E称为边集，其中的元素叫图G的边， [3]Ψ是从边集E到顶点集V中的有序或无序的元素 偶对构成集合的映射，称为关联函数 例1设G=(V,E,Ψ)，其中 ={v1,v2,v3,v4} E-e1,e2.e3 es es), Ψ(e)=y2,Ψ(e2)=y3,Y(e)=v4,Y(e4)=y4,Y(e)=v44 G的图解如图

定义 有序三元组G=(V,E, )  称为一个图,如果： [1] V={ , , , } 1 2 n v v  v 是有限非空集，V 称为顶点集， 其中的元素叫图 G 的顶点. [2] E 称为边集，其中的元素叫图 G 的边. [3]  是从边集 E 到顶点集 V 中的有序或无序的元素 偶对构成集合的映射，称为关联函数. 例1 设 G=(V,E, )，其中 V={v1 ,v2 , v3 , v4 }， E={e1, e2 , e3, e4, e5 }, 1 1 2 2 1 3 3 1 4 4 1 4 5 4 4  =  =  =  =  = ( ) , ( ) , ( ) , ( ) , ( ) e v v e v v e v v e v v e v v . G 的图解如图 图的定义

定义在图G中，与V中的有序偶.以对应的边，称为图的有向边 (或弧)，而与V中顶点的无序偶y相对应的边，称为图的无 向边每一条边都是无向边的图，叫无向图；每一条边都是有向 边的图，称为有向图；既有无向边又有有向边的图称为混合图. 定义若将图G的每一条边e都对应一个实数w(e),则称w(e)为边的 权，并称图G为赋权图. 规定用记号v和ε分别表示图的顶点数和边数

定义 在图 G 中，与 V 中的有序偶(vi， vj )对应的边 e ，称为图的有向边 （或弧），而与 V 中顶点的无序偶 vi vj 相对应的边e ，称为图的无 向边.每一条边都是无向边的图，叫无向图；每一条边都是有向 边的图，称为有向图；既有无向边又有有向边的图称为混合图. 定义 若将图 G 的每一条边e 都对应一个实数 w( e )，则称 w( e )为边的 权，并称图 G 为赋权图. 规定用记号 和 分别表示图的顶点数和边数

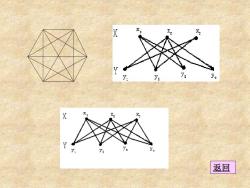
el 2 es 常用术语： e (1)端点相同的边称为环 (2)若一对顶点之间有两条以上的边联结，则这些边称为重边， (3)有边联结的两个顶点称为相邻的顶点，有一个公共端点的边 称为相邻的边. (4)边和它的端点称为互相关联的。 (5)既没有环也没有平行边的图，称为简单图 (6)任意两顶点都相邻的简单图，称为完备图，记为K,其中n 为顶点的数目. (7)若=XUY,X⌒Y=Φ，且X中任两顶点不相邻，Y中任两顶 点不相邻，则称G为二元图：若X中每一顶点皆与Y中一切顶点 相邻，则G称为完备二元图，记为Kmn,其中m,n分别为X与Y的项 点数目

常用术语： （１）端点相同的边称为环． （２）若一对顶点之间有两条以上的边联结，则这些边称为重边． （３）有边联结的两个顶点称为相邻的顶点，有一个公共端点的边 称为相邻的边． （４）边和它的端点称为互相关联的． （５）既没有环也没有平行边的图，称为简单图． （６）任意两顶点都相邻的简单图，称为完备图，记为 Kn，其中 n 为顶点的数目． ( 7)若 V=X Y，X Y= ，且 X 中任两顶点不相邻，Y 中任两顶 点不相邻，则称 G 为二元图；若 X 中每一顶点皆与 Y 中一切顶点 相邻，则 G 称为完备二元图，记为 Km,n，其中 m,n 分别为 X 与 Y 的顶 点数目．

返回

返回

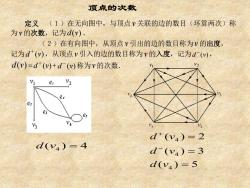
顶点的次数 定义(1)在无向图中，与顶点v关联的边的数目（环算两次）称 为v的次数，记为d(v). (2)在有向图中，从顶点v引出的边的数目称为v的出度， 记为d(y),从顶点v引入的边的数目称为v的入度，记为d(w), d(v)=d(v)+d厂(v)称为v的次数 e, V2 ez d+(y4)=2 d(y4)=4 d(y4)=3 d(v4)=5

顶点的次数 定义 （１）在无向图中，与顶点 v 关联的边的数目（环算两次）称 为v 的次数，记为d v( ) ． （２）在有向图中，从顶点v 引出的边的数目称为v 的出度， 记为d v( ) ＋ ，从顶点v 引入的边的数目称为v 的入度，记为d v( ) － ， d v( ) = d v( ) ＋ + d v( ) － 称为 v 的次数． 4 d v( ) 4 = ( ) 5 ( ) 3 ( ) 2 4 4 4 = = = − + d v d v d v

定理1 ∑d()=28(G) vel/(G) 推论1任何图中奇次顶点的总数必为偶数. 例在一次聚会中，认识奇数个人的人数一定是偶数 返回

定理１ ( ) 2 ( ) ( ) d v G v V G  =   推论１ 任何图中奇次顶点的总数必为偶数． 例 在一次聚会中，认识奇数个人的人数一定是偶数. 返回

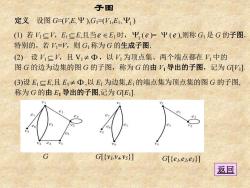
子图 定义设图G=(V,E,平)，G1=(W,E1,平1) (1)若1sV,EsE,且当e∈E时，Y(e)=Ψ(e),则称G1是G的子图. 特别的，若V=V,则G称为G的生成子图. (2)设V三，且V1≠Φ，以V1为顶点集、两个端点都在中的 图G的边为边集的图G的子图，称为G的由导出的子图，记为GV] (3)设E1三E,且E1≠①，以E1为边集，E1的端点集为顶点集的图G的子图， 称为G的由E导出的子图，记为GE] G[{v,v4v5}] GHeLe2e3)] 返回

子图 定义 设图 G=(V,E, ),G1 =(V1,E1,1 ) (1) 若 V1 V，E1 E,且当e E1 时，1 ( e )=  ( e ),则称 G1是 G 的子图． 特别的，若 V1 =V，则 G1称为 G 的生成子图． (2) 设 V1 V，且 V1   ，以 V1为顶点集、两个端点都在 V1中的 图 G 的边为边集的图 G 的子图，称为 G 的由 V1导出的子图，记为 G[V1 ]. (3)设 E1 E,且 E1   ,以 E1为边集,E1的端点集为顶点集的图 G 的子图, 称为 G 的由 E1导出的子图,记为 G[E1 ]. G G[{v1,v4,v5 }] G[{e1,e2,e3 }] 返回