《数学建模与数学实验》教学教学资源（案例）人口预报问题

数学建模实例：人口预报问题 1.问题 人口问题是当前世界上人们最关心的问题之一认识人口数量的变化规律， 作出较准确的预报，是有效控制人口增长的前提下面介绍两个最基本的人口棋 型，并利用表1给出的近两百年的美国人口统计数据，对模型做出检验，最后 用它预报2000年、2010年美国人口. 表1美国人口统计数据 年（公元）1790 180018101820183018401850 人口（百万） 3.9 5.3 12 9.612.917.1 23.2 年（公元） 1860 18701880 1890 1900 19101920 人口（百万） 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年（公元) 1930 1940 1950 1960 1970 1980 1990 人口（百万） 123.2 131.7150.7179.3204.0 226.5251.4 2.指数增长模型（马尔萨斯人口模型） 此模型由英国人口学家马尔萨斯(Malthus1766一1834)于1798年提出. 山假设：人口增长率r是常数（或单位时间内人口的增长量与当时的人口成正 比) 2☑叫建立模型：记时刻0时人口数为m,时刻1的人口为0，由于量大， 可视为连续、可徽函数t到1+时间内人口的增量为： t+-0=n0 于是x)满足微分方程

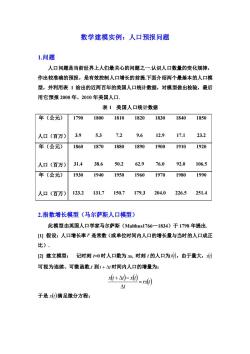
数学建模实例：人口预报问题 1.问题 人口问题是当前世界上人们最关心的问题之一.认识人口数量的变化规律， 作出较准确的预报，是有效控制人口增长的前提.下面介绍两个最基本的人口模 型，并利用表 1 给出的近两百年的美国人口统计数据，对模型做出检验，最后 用它预报 2000 年、2010 年美国人口. 表 1 美国人口统计数据 年（公元） 人口（百万） 1790 3.9 1800 5.3 1810 7.2 1820 9.6 1830 12.9 1840 17.1 1850 23.2 年（公元） 人口（百万） 1860 31.4 1870 38.6 1880 50.2 1890 62.9 1900 76.0 1910 92.0 1920 106.5 年（公元） 人口（百万） 1930 123.2 1940 131.7 1950 150.7 1960 179.3 1970 204.0 1980 226.5 1990 251.4 2.指数增长模型（马尔萨斯人口模型） 此模型由英国人口学家马尔萨斯（Malthus1766—1834）于 1798 年提出. [1] 假设：人口增长率 r 是常数（或单位时间内人口的增长量与当时的人口成正 比）. [2] 建立模型： 记时刻 t=0 时人口数为 x0, 时刻 t 的人口为 x(t) ，由于量大， x(t) 可视为连续、可微函数.t 到 t + t 时间内人口的增量为： ( ) ( ) rx(t) t x t t x t =  +  − 于是 x(t) 满足微分方程：

dx dt =Fx (1) ()=xo 3模型求解：解微分方程(1)得 x(t)=xe" (2) 表明：t→0时，x0→0(r>0). 4模型的参数估计： 要用模型的结果(2)来预报人口，必须对其中的参数r进行估计，这可以 用表11的数据通过拟合得到拟合的具体方法见本书第16章或第18章 通过表中1790一1980的数据拟合得：r-0.307. 5模型检验： 将x=3.9,r-0.307代入公式(2)，求出用指数增长模型预测的1810一1920 的人口数，见表2 表2美国实际人口与按指数增长模型计算的人口比较 年 实际人可 指数增长模型 (公元) (百万) 预测人口（百万） 误差（%) 1790 3.9 1800 53 1810 7.2 1.4 1820 9.6 10.0 1保30 12.9 1840 17.1 1850 232 256 103 1860 .4 35.0 10.8 1870 386 478 23.8 180 02 655 30.5 1890 1900 0 89.6 424 122.5 612 1910 92.0 167.6 82.1 1920 106.5 229.3 115.3

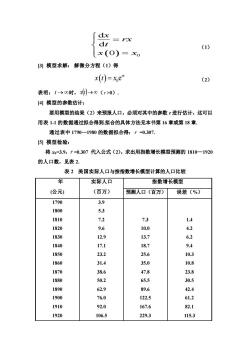
( ) 0 d d 0 x rx t x x   =    = （1） [3] 模型求解： 解微分方程（1）得 ( ) 0 e rt x t x = （2） 表明： t →  时， x(t)→ （ r >0）. [4] 模型的参数估计： 要用模型的结果（2）来预报人口，必须对其中的参数 r 进行估计，这可以 用表 1-1 的数据通过拟合得到.拟合的具体方法见本书第 16 章或第 18 章. 通过表中 1790—1980 的数据拟合得： r =0.307. [5] 模型检验： 将 x0=3.9，r =0.307 代入公式（2），求出用指数增长模型预测的 1810—1920 的人口数，见表 2. 表 2 美国实际人口与按指数增长模型计算的人口比较 年 (公元) 实际人口 （百万） 指数增长模型 预测人口（百万） 误差（%） 1790 3.9 1800 5.3 1810 7.2 7.3 1.4 1820 9.6 10.0 4.2 1830 12.9 13.7 6.2 1840 17.1 18.7 9.4 1850 23.2 25.6 10.3 1860 31.4 35.0 10.8 1870 38.6 47.8 23.8 1880 50.2 65.5 30.5 1890 62.9 89.6 42.4 1900 76.0 122.5 61.2 1910 92.0 167.6 82.1 1920 106.5 229.3 115.3

从表2可看出，1810一1870间的预测人口数与实际人口数吻合较好，但1880 年以后的误差越来越大 分析原因，该棋型的结果说明人口将以指数规律无限增长而事实上，随着人 口的增加，自然资源、环境条件等因素对人口增长的限制作用越来越显著如果 当人口较少时人口的自然增长率可以看作常数的话，那么当人口增加到一定数 量以后，这个增长率就要随着人口增加而减少.于是应该对指数增长模型关于人 口净增长率是常数的假设进行修政下面的模型是在修政的模型中著名的一个 3.阻滞增长模型(logistic模型) 山假设： (a)人口增长率r为人口利的函数（减函数），最简单假定 =r-,r,5>0(线性函数)，r叫做固有增长率 (b)自然资源和环境条件年容纳的最大人口容量xm· [2建立模型 当x=x时，增长率应为0，即r(x)=0,于是S= ，代入=r-m (3) 将(3)式代入(1)得： dx 模型： (4) x(0)= 3模型的求解：解方程组(4)得 x1= (5) m 根据方程（作出出-x线图，见，由该图可看出人口端长率随人 口数的变化规律根据结果(5)作出x-1曲线，见图2，由该图可看出人口数随

从表 2 可看出，1810—1870 间的预测人口数与实际人口数吻合较好，但 1880 年以后的误差越来越大. 分析原因，该模型的结果说明人口将以指数规律无限增长.而事实上，随着人 口的增加，自然资源、环境条件等因素对人口增长的限制作用越来越显著.如果 当人口较少时人口的自然增长率可以看作常数的话，那么当人口增加到一定数 量以后，这个增长率就要随着人口增加而减少.于是应该对指数增长模型关于人 口净增长率是常数的假设进行修改.下面的模型是在修改的模型中著名的一个. 3. 阻滞增长模型（logistic 模型） [1]假设： （ a ） 人 口 增 长 率 r 为人口 x(t) 的函数 r(x) （ 减 函 数 ）， 最 简 单 假 定 r(x) = r − sx, r,s  0 （线性函数）， r 叫做固有增长率. （b）自然资源和环境条件年容纳的最大人口容量 m x . [2]建立模型： 当 m x x = 时，增长率应为 0，即 r x( m ) =0，于是 m r s x = ，代入 r(x) = r − sx 得： ( ) m 1 x r x r x   = −     （3） 将（3）式代入（1）得： 模型： ( ) m 0 1 0 dx x r x dt x x x     = −       =  （4） [3] 模型的求解： 解方程组（4）得 ( ) m m 0 1 1 rt x x t x e x − =   + −     （5） 根据方程（4）作出 d d x x t − 曲线图，见图 1，由该图可看出人口增长率随人 口数的变化规律.根据结果（5）作出 x-t 曲线，见图 2，由该图可看出人口数随

时间的变化规律 错误！ 未定 图21曲线图 ④模型的参数估计： 利用表1中1790一1980的数据对r和x拟合得：r=0.2072,xm=464. 5棋型检验： 将r=0.2072,x。=464代入公式(5)，求出用指数增长模型预测的1800 1990的人口数，见表3第3、4列 也可将方程(4)离散化，得 +)=x0+Ax=0+rI-0x0 0,1,2,(⑥ 用公式(6)预测1800一1990的人口数，结果见表3第5、6列. 表3美国实际人口与按阻滞增长模型计算的人口比较 实际 阻滞增长模型 人口 公式(5) 公式(6) (百万) 预测人口（百列误差(%） 预测人口（百）误差（%) 1790 3.9 1800 5.3 5.9025 0.1137 3.9000 0.2642 1810 7.2614 0.0085 6.5074 0.0962 1820 9 8.9332 0.0695 8.6810 0.0957 1830 12.9 10.9899 0.1481 11.4153 0.1151 1840 17.1 13.5201 0.2094 15.1232 0.1156

时间的变化规律. [4] 模型的参数估计： 利用表 1 中 1790—1980 的数据对 r 和 m x 拟合得： r =0.2072, m x =464. [5] 模型检验： 将 r =0.2072, m x =464 代入公式（5），求出用指数增长模型预测的 1800— 1990 的人口数，见表 3 第 3、4 列. 也可将方程（4）离散化，得 ) ( ) ( ) ( 1) ( ) ( ) (1 x t x x t x t x t x x t r m + = +  = + − t=0,1,2,., (6) 用公式（6）预测 1800—1990 的人口数，结果见表 3 第 5、6 列. 表 3 美国实际人口与按阻滞增长模型计算的人口比较 年 实际 人口 (百万) 阻滞增长模型 公式（5） 公式（6） 预测人口(百万) 误差（%） 预测人口(百万) 误差（%） 1790 3.9 1800 5.3 5.9025 0.1137 3.9000 0.2642 1810 7.2 7.2614 0.0085 6.5074 0.0962 1820 9.6 8.9332 0.0695 8.6810 0.0957 1830 12.9 10.9899 0.1481 11.4153 0.1151 1840 17.1 13.5201 0.2094 15.1232 0.1156 O xm 2 xm x 错 误 ! 未 定 义 书 签。 图 1 dx x dt − 曲线图 x xm x0 2 0 x O t 图 2 x-t 曲线图

1850 23.2 16.6328 0.2831 19.8197 0.1457 1860 31.4 20.4621 0.3483 26.5228 0.1553 1870 38.6 25.1731 0.3478 35.4528 0.0815 1880 50.2 30.9687 0.3831 43.5329 0.1328 1890 62.9 38.0986 0.3943 56.1884 0.1067 1900 76.0 46.8699 0.3833 70.1459 0.0770 1910 92.0 57.6607 0.3733 84.7305 0.0790 1920 106.5 70.9359 0.3339 102.4626 0.0379 1930 123.2 87.2674 0.2917 118.9509 0.0345 1940 131.7 107.3588 0.1848 137.8810 0.0469 1950 150.7 132.0759 0.1236 148.7978 0.0126 1960 179.3 162.4835 0.0938 170.2765 0.0503 1970 204.0 199.8919 0.0201 201.1772 0.0138 1980 226.5 245.9127 0.0857 227.5748 0.0047 1990 251.4 302.5288 0.2034 250.4488 0.0038 6模型应用： 现应用该模型预测人口.用表1中1790一1990年的全部数据重新估计参 数，可得r=0.2083,xm=457.6.用公式(6)作预测得： x(2000=275;x(2010)=297.9 也可用公式(5)进行预测

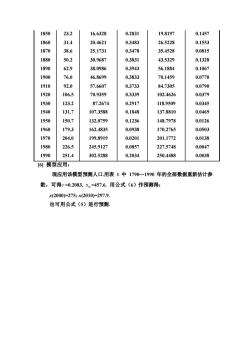
1850 23.2 16.6328 0.2831 19.8197 0.1457 1860 31.4 20.4621 0.3483 26.5228 0.1553 1870 38.6 25.1731 0.3478 35.4528 0.0815 1880 50.2 30.9687 0.3831 43.5329 0.1328 1890 62.9 38.0986 0.3943 56.1884 0.1067 1900 76.0 46.8699 0.3833 70.1459 0.0770 1910 92.0 57.6607 0.3733 84.7305 0.0790 1920 106.5 70.9359 0.3339 102.4626 0.0379 1930 123.2 87.2674 0.2917 118.9509 0.0345 1940 131.7 107.3588 0.1848 137.8810 0.0469 1950 150.7 132.0759 0.1236 148.7978 0.0126 1960 179.3 162.4835 0.0938 170.2765 0.0503 1970 204.0 199.8919 0.0201 201.1772 0.0138 1980 226.5 245.9127 0.0857 227.5748 0.0047 1990 251.4 302.5288 0.2034 250.4488 0.0038 [6] 模型应用： 现应用该模型预测人口.用表 1 中 1790—1990 年的全部数据重新估计参 数，可得 r =0.2083, m x =457.6. 用公式（6）作预测得： x(2000)=275; x(2010)=297.9. 也可用公式（5）进行预测