《数学建模与数学实验》教学教学资源（案例）配方问题

配方问题 在化工、医药、日常膳食等方面都经常涉及到配方问题.在不考虑各种成分 之间可能发生某些化学反应时，配方问题可以用向量和线性方程组来建模 图5日常膳食搭配 图6几种常见的作料 【模型准备】一种佐料由四种原料A、B、C、D混合而成.这种佐料现有两种规 格，这两种规格的佐料中，四种原料的比例分别为2：3：1：1和1：2：12.现在需要四 种原料的比例为4：7：3：5的第三种规格的佐料.问：第三种规格的佐料能否由前 两种规格的佐料按一定比例配制而成？ 【模型假设】()假设四种原料混合在一起时不发生化学变化，(2)假设四种原 料的比例是按重量计算的.()假设前两种规格的佐料分装成袋，比如说第一种 规格的佐料每袋净重7克（其中A、B、C、D四种原料分别为2 克，1克， 克)，第二种规格的佐料每袋净重6克（其中A、B、C、D四种原料分别为1克，2 克，1克，2克). 【模型建立】根据已知数据和上述假设，可以进一步假设将x袋第一种规格的 佐料与y袋第二种规格的佐料混合在一起，得到的混合物中A、B、C、D四种原 料分别为4克，7克，3克，5克，则有以下线性方程组 x+y= x+2y=5 【模型求解】上述线性方程组的增广矩阵

配方问题 在化工、医药、日常膳食等方面都经常涉及到配方问题. 在不考虑各种成分 之间可能发生某些化学反应时, 配方问题可以用向量和线性方程组来建模. 图 5 日常膳食搭配 图 6 几种常见的作料 【模型准备】一种佐料由四种原料 A、B、C、D 混合而成. 这种佐料现有两种规 格, 这两种规格的佐料中, 四种原料的比例分别为 2:3:1:1 和 1:2:1:2. 现在需要四 种原料的比例为 4:7:3:5 的第三种规格的佐料. 问: 第三种规格的佐料能否由前 两种规格的佐料按一定比例配制而成? 【模型假设】 (1) 假设四种原料混合在一起时不发生化学变化. (2) 假设四种原 料的比例是按重量计算的. (3) 假设前两种规格的佐料分装成袋, 比如说第一种 规格的佐料每袋净重 7 克(其中 A、B、C、D 四种原料分别为 2 克, 3 克, 1 克, 1 克), 第二种规格的佐料每袋净重 6 克(其中 A、B、C、D 四种原料分别为 1 克, 2 克, 1 克, 2 克). 【模型建立】 根据已知数据和上述假设, 可以进一步假设将 x 袋第一种规格的 佐料与 y 袋第二种规格的佐料混合在一起, 得到的混合物中 A、B、C、D 四种原 料分别为 4 克, 7 克, 3 克, 5 克, 则有以下线性方程组 2 4, 3 2 7, 3, 2 5. x y x y x y x y  + =  + =  + =   + = 【模型求解】上述线性方程组的增广矩阵

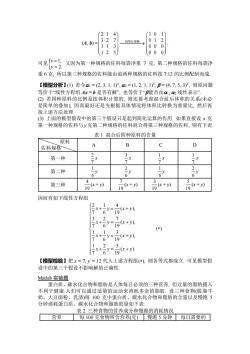
214 32 09 (A.B)= 初学行变换、 113 000 125 000 可见仁2又因为第一种规格的佐料每袋净重7克，第二种规格的佐料每袋净 重6克，所以第三种规格的佐料能由前两种规格的佐料按7：12的比例配制而成 【模型分析】)若令=(2,3,1,1，m=(1,2,1,1),B=(4,7,5,3),则原问题 等价于“线性方程组Ax=b是否有解”，也等价于“能否由a,线性表示 (②)若四种原料的比例是按体积计算的，则还要考虑混合前后体积的关系（未必 是简单的叠加)，因而最好还是先根据具体情况将体积比转换为重量比，然后再 按上述方法处理 面的模型假设中的第三个假设只是起到简化运算的作用如果直接设克一 一种规格的佐料与y克第二种规格的佐料混合得第三种规格的佐料，则有下表 表1混合后四种原料的含量 原料 佐料规格 B D 第一种 x 第二种 第三种 西r+列 r+功 因而有如下线性方程组 6s 7 1 3 【模型检验】把x=7,y=12代入上述方程组()，则各等式都成立.可见模型假 设中的第三个假设不影响解的正确性」 Matlab实验题 蛋白质、碳水化合物和脂肪是人体每日必须的三种营养，但过量的脂肪摄入 不利于健康.人们可以通过适量的运动来消耗多余的脂肪.设三种食物（脱脂牛 奶、大豆面粉、乳清)每100克中蛋白质、碳水化合物和脂肪的含量以及慢跑5 分钟消耗蛋白质、碳水化合物和脂肪的量如下表 表2三种食物的营养成分和慢跑的消耗情况 营养 每100克食物所含营养（克）慢跑5分钟每日需要的☐

(A, b) = 2 1 4 3 2 7 1 1 3 1 2 5           ⎯⎯⎯⎯→ 初等行变换 1 0 1 0 1 2 0 0 0 0 0 0           , 可见  1, 2. x y = = 又因为第一种规格的佐料每袋净重 7 克, 第二种规格的佐料每袋净 重 6 克, 所以第三种规格的佐料能由前两种规格的佐料按 7:12 的比例配制而成. 【模型分析】(1) 若令1 = (2, 3, 1, 1)T, 2 = (1, 2, 1, 1)T,  = (4, 7, 5, 3)T, 则原问题 等价于“线性方程组 Ax = b 是否有解”, 也等价于“能否由1, 2 线性表示”. (2) 若四种原料的比例是按体积计算的, 则还要考虑混合前后体积的关系(未必 是简单的叠加), 因而最好还是先根据具体情况将体积比转换为重量比, 然后再 按上述方法处理. (3) 上面的模型假设中的第三个假设只是起到简化运算的作用. 如果直接设 x 克 第一种规格的佐料与 y 克第二种规格的佐料混合得第三种规格的佐料, 则有下表 表 1 混合后四种原料的含量 原料 佐料规格 A B C D 第一种 2 7 x 3 7 x 1 7 x 1 7 x 第二种 1 6 y 2 6 y 1 6 y 2 6 y 第三种 4 19 (x + y) 7 19 (x + y) 3 19 (x + y) 5 19 (x + y) 因而有如下线性方程组 2 1 4 ( ), 7 6 19 3 2 7 ( ), 7 6 19 1 1 3 ( ), 7 6 19 1 2 5 ( ). 7 6 19 x y x y x y x y x y x y x y x y  + = +    + = +    + = +    + = +  () 【模型检验】把 x = 7, y = 12 代入上述方程组(), 则各等式都成立. 可见模型假 设中的第三个假设不影响解的正确性. Matlab 实验题 蛋白质、碳水化合物和脂肪是人体每日必须的三种营养, 但过量的脂肪摄入 不利于健康.人们可以通过适量的运动来消耗多余的脂肪. 设三种食物(脱脂牛 奶、大豆面粉、乳清)每 100 克中蛋白质、碳水化合物和脂肪的含量以及慢跑 5 分钟消耗蛋白质、碳水化合物和脂肪的量如下表. 表 2 三种食物的营养成分和慢跑的消耗情况 营养 每 100 克食物所含营养(克) 慢跑 5 分钟 每日需要的

牛奶大豆面粉乳清消耗量（克）营养量（克） 蛋白质 36 51 13 10 33 碳水化合物 52 34 74 20 45 脂肪 10 7 1 15 可怎样安排饮食和运动才能实现每日的营养需求？

牛奶 大豆面粉 乳清 消耗量(克) 营养量(克) 蛋白质 36 51 13 10 33 碳水化合物 52 34 74 20 45 脂肪 10 7 1 15 3 问怎样安排饮食和运动才能实现每日的营养需求?