《数学建模与数学实验》教学教学资源（PPT课件）第9讲 数据的统计分析与描述

数学建模与数学实验 数据的统计描述和分析

数学建模与数学实验 数据的统计描述和分析

实验目的 1.直观了解统计基本内容 2.掌握用数学软件包求解统计问题 卖验内容 1.统计的基本理论. 2.用数学软件包求解统计问题 3.实验作业

实验目的 实验内容 2．掌握用数学软件包求解统计问题. 1．直观了解统计基本内容. 1．统计的基本理论. 3．实验作业. 2．用数学软件包求解统计问题

数据的统计描述和分析 统计的基本概念 参数估计 假发验

统计的基本概念 参数估计 假设检验 数据的统计描述和分析

一、统计量 1. 表示位置的统计量一平均值和中位数 7 平均值（或均值，数学期望）：刀=∑X n i= 中位数：将数据由小到大排序后位于中间位置的那个数值 2.表示变异程度的统计量一标准差、方差和极差 标准差，三(X小 它是各个数据与均值偏离程度的度量 方差：标准差的平方 极差：样本中最大值与最小值之差

1. 表示位置的统计量—平均值和中位数. 平均值（或均值，数学期望）： = = n i Xi n X 1 1 中位数：将数据由小到大排序后位于中间位置的那个数值. 2. 表示变异程度的统计量—标准差、方差和极差. 标准差： 2 1 1 2 ( ) ] 1 1 [ = − − = n i Xi X n s 它是各个数据与均值偏离程度的度量. 方差：标准差的平方. 极差：样本中最大值与最小值之差. 一、统计量

3.表示分布形状的统计量一偏度和峰度 偏度：8=号2X-X0降度：：2(x-对 偏度反映分布的对称性，g1>0称为右偏态，此时数据位于均值 右边的比位于左边的多；g1<0称为左偏态，情况相反：而g1接近0 则可认为分布是对称的 峰度是分布形状的另一种度量，正态分布的峰度为3，若g2比3 大很多，表示分布有沉重的尾巴，说明样本中含有较多远离均值的数 据，因而峰度可用作衡量偏离正态分布的尺度之一 4k阶原点矩：y=1∑Xk阶中心矩：U,=1∑(X,-X) n i=l ni=

3. 表示分布形状的统计量—偏度和峰度 偏度： = = − n i Xi X s g 1 3 1 3 ( ) 1 峰度： = = − n i Xi X s g 1 4 2 4 ( ) 1 偏度反映分布的对称性，g1 >0 称为右偏态，此时数据位于均值 右边的比位于左边的多；g1 <0 称为左偏态，情况相反；而 g1接近 0 则可认为分布是对称的. 峰度是分布形状的另一种度量，正态分布的峰度为 3，若 g2比 3 大很多，表示分布有沉重的尾巴，说明样本中含有较多远离均值的数 据，因而峰度可用作衡量偏离正态分布的尺度之一. 4. k 阶原点矩： = = n i k k Xi n V 1 1 k 阶中心矩： = = − n i k k Xi X n U 1 ( ) 1

二、分布函数的近似求法 1整理资料：把样本值x1,2,.,xn进行分组，先将它们依大小次序排列， 得x≤x2≤.≤x,在包含[x,x]的区间[a,b]内插入一些等分点： a<x<x2<.<x,<b,注意要使每一个区间(x,x](=1,2,.,n-1) 内都有样本观测值x(=1,2,.,-1)落入其中 2.求出各组的频数和频率：统计出样本观测值在每个区间(x,x]中出 现的次数口，它就是这区间或这组的频数计算频率f= n 3作频率直方图：在直角坐标系的横轴上，标出x,x2,.,xn各点，分别以 (x,x]为底边，作高为的矩形，△x=x1-x,1=1,2,n-1,即得 △X 频率直方图

二、分布函数的近似求法 1.整理资料： 把样本值 x1，x2，.，xn进行分组，先将它们依大小次序排列， 得 * * 2 * 1 n x  x  x .在包含[ , ] * * 1 n x x 的区间[a，b]内插入一些等分点： , ' ' 2 ' a  x1  x    xn  b 注意要使每一个区间( , ] ' 1 ' i i+ x x （i=1，2，.，n-1） 内都有样本观测值 xi（i=1，2，.，n-1）落入其中. 2.求出各组的频数和频率：统计出样本观测值在每个区间( , ] ' 1 ' i i+ x x 中出 现的次数 i n ，它就是这区间或这组的频数.计算频率 n n f i i = . 3.作频率直方图：在直角坐标系的横轴上，标出 ' ' 2 ' 1 , , , n x x  x 各点，分别以 ( , ] ' 1 ' i i+ x x 为底边，作高为 ' i i x f  的矩形， , 1,2, , 1 ' ' 1 ' xi = xi+ − xi i =  n − ,即得 频率直方图

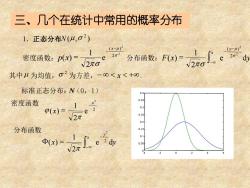
三、几个在统计中常用的概率分布 1.正态分布N(4,o2) 1 (x-4)2 (y-4)2 密度函数：p(x)= √2πo 其中4为均值，σ2为方差，-0<x<+o0 标准正态分布：N(0,1) 0.4 密度函数 0.35 p(x)= W2π 0 分布函数 Φ(x)= 4

三、几个在统计中常用的概率分布 -4 -2 0 2 4 6 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 1．正态分布 ( , ) 2 N m s 密度函数： 2 2 2 ( ) 2 1 ( ) s m ps − − = x p x e 分布函数：F x e dy y x 2 2 2 ( ) 2 1 ( ) s m ps − − −  = 其中m 为均值， 2 s 为方差，−   x  +. 标准正态分布：N（0，1） 密度函数 2 2 2 1 ( ) x x e − = p j x e dy y x 2 2 2 1 ( ) − − F = p 分布函数

2.X2分布x2() 若随机变量X1,X2,.,Xn相互独立，都 服从标准正态分布N(0,1),则随机变量 Y=Xi+X2++X2 服从自由度为n的x2分布，记为Y~x2(n). Y的均值为n,方差为2n 校

0 5 10 15 20 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 2. 2  分布 2  (n) 若随机变量 X1，X2，.，Xn 相互独立，都 服从标准正态分布 N（0，1），则随机变量 Y= 2 2 2 2 X1 + X ++ Xn 服从自由度为 n 的 2  分布，记为 Y~ 2  （n）. Y 的均值为 n，方差为 2n

3.t分布tn) 若X~N(0,1),Y~X2(n,且相互独 立，则随机变量 T=_Y n 服从自由度为n的t分布，记为T~t(n) t(20)分布的密度函数曲线和N(0,1)的 曲线形状相似.理论上n→o时，Tt(n)→N(0,1), 0.0s

3. t 分布 t（n） 若 X~N（0，1），Y~ 2  （n），且相互独 立，则随机变量 n Y X T = 服从自由度为 n 的 t 分布，记为 T~t（n）. t（20）分布的密度函数曲线和 N（0，1）的 曲线形状相似.理论上 n→ 时，T~t（n）→N（0，1）. -6 -4 -2 0 2 4 6 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

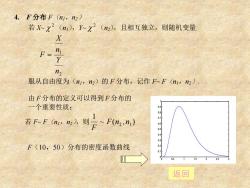
4.F分布F(n,n2） 若Xx2(m),Yx2(n2),且相互独立，则随机变量 X 九 F= n2 服从自由度为(n1,n2)的F分布，记作F~F(n1,n2) 由F分布的定义可以得到F分布的 一个重要性质： 若rFm,则Fmn) 9订65432 F(10,50)分布的密度函数曲线 0 0.5 2.5 返回

4. F 分布 F（n1，n2） 若 X~ 2  （n1），Y~ 2  （n2），且相互独立，则随机变量 2 1 n Y n X F = 服从自由度为（n1，n2）的 F 分布，记作 F~ F（n1，n2）. 由 F 分布的定义可以得到 F 分布的 一个重要性质： 若 F~ F（n1，n2），则 ~ ( , ) 1 F n2 n1 F 0 0.5 1 1.5 2 2.5 3 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 返回 F（10，50）分布的密度函数曲线