《数学建模与数学实验》课程教学资源（PPT讲稿）数学建模几种创新思维方法

重要的科学思维方式之一是创新 思维，创新思维是创新能力的核心 与灵魂。 数学模型(E.A.Bendar定义)： 关于部分现实世界为一定目的而做的 抽象、简化的数学结构

数学模型(E.A.Bendar 定义)： 关于部分现实世界为一定目的而做的 抽象、简化的数学结构。 重要的科学思维方式之一是创新 思维，创新思维是创新能力的核心 与灵魂

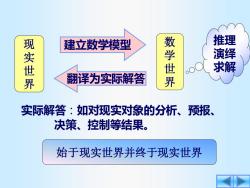
建立数学模型 推理 现实世界 数学世界 演绎 求解 翻译为实际解答 实际解答：如对现实对象的分析、预报、 决策、控制等结果。 始于现实世界并终于现实世界

现 实 世 界 数 学 世 界 建立数学模型 推理 演绎 求解 翻译为实际解答 实际解答：如对现实对象的分析、预报、 决策、控制等结果。 始于现实世界并终于现实世界

数学模型是现实世界与数学世界的理想桥梁， 怎样构架这座桥梁？ *数学建模没有普遍适用的方法与技巧. *有一些普遍适用的思想方法与思维方式、 整个数学建模过程由若干个有 明显差别的阶段性工作组成

数学模型是现实世界与数学世界的理想桥梁， * 数学建模没有普遍适用的方法与技巧. * 有一些普遍适用的思想方法与思维方式. 整个数学建模过程由若干个有 明显差别的阶段性工作组成 怎样构架这座桥梁？

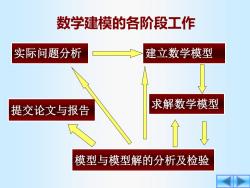
数学建模的各阶段工作 实际问题分析 建立数学模型 提交论文与报告 求解数学模型 ↑↓ 模型与模型解的分析及检验

求解数学模型 实际问题分析 建立数学模型 提交论文与报告 模型与模型解的分析及检验 数学建模的各阶段工作

此流程具有指导意义，应注意 *流程应用是弹性的，切不能生搬硬套， *建模过程往往是一个反复循环的过程. 本章基本上按照此流程来介绍数学建 模的方法

此流程 具有指导意义 ，应注意 * 流程应用是弹性的，切不能生搬硬套. 本章基本上按照此流程来介绍数学建 模的方法。 * 建模过程往往是一个反复循环的过程

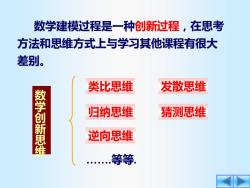
数学建模过程是一种创新过程，在思考 方法和思维方式上与学习其他课程有很大 差别。 类比思维 发散思维 数学创新思维 归纳思维 猜测思维 逆向思维 .等等

数学建模过程是一种创新过程，在思考 方法和思维方式上与学习其他课程有很大 差别。 数 学 创 新 思 维 .等等. 类比思维 归纳思维 逆向思维 发散思维 猜测思维

掌握几类方法：问题解决法、思想表达 法、创造发明法 对于创造能力 的培养不可或 方法的共同特点： 缺 不轻易否定别人的意见 怀疑一般常识， 努力发现别人尚未察觉的事物等 以下介绍几种（个体和集体的)创造 性思维方法

掌握几类方法：问题解决法、思想表达 法、创造发明法. 方法的共同特点： 不轻易否定别人的意见， 怀疑一般常识， 努力发现别人尚未察觉的事物等 以下介绍几种（个体和集体的）创造 性思维方法 对于创造能力 的培养不可或 缺

一、打开思路的方法 发散性思维和猜测思维是创造性思维方 式的重要组成部分 面对新问题，应尽量打开自己的思路： 1.不要轻易沿一条思路深入，不要轻易 做出结论. 2.尽量多一些想法，多一些猜测。 思考、思考、再思考

一、打开思路的方法 面对新问题，应尽量打开自己的思路： 发散性思维和猜测思维是创造性思维方 式的重要组成部分 1. 不要轻易沿一条思路深入，不要轻易 做出结论. 2. 尽量多一些想法，多一些猜测。 思考、思考、再思考

提问题法 帮助展开思路的方法 关键词联想法 1.提问题法 借助于一系列问题来展开思路. 面临难题，束手无策时通过提出一系列问 题来导出一些想法或一个好的方案 如： ()这个问题和什么问题相类似？ (2)假如变动问题的某些条件将会怎样？

帮助展开思路的方法： 关键词联想法 提问题法 1.提问题法 面临难题, 束手无策时通过提出一系列问 题来导出一些想法或一个好的方案. 如： (l) 这个问题和什么问题相类似？ (2) 假如变动问题的某些条件将会怎样？ 借助于一系列问题来展开思路

(3)将问题分解成若干部分再考虑会怎样？ (4)重新组合又会怎样？ 为进一步打开思路可提以下问题： (⑤)我们还可以做什么工作？ (6)有无需要进一步完善的内容？ (⑦)可否换一种数学工具来解决此问题？ 针对问题和初始方案可以先设计出类似的 问题清单，然后反复展开

(4) 重新组合又会怎样？ (3) 将问题分解成若干部分再考虑会怎样？ 为进一步打开思路可提以下问题： (5) 我们还可以做什么工作？ (6)有无需要进一步完善的内容？ (7) 可否换一种数学工具来解决此问题？ 针对问题和初始方案可以先设计出类似的 问题清单，然后反复展开