《线性代数》课程PPT教学课件（同济第五版）第2章 矩阵及其运算 2.1 矩阵

矩陈及其适氧 第一节矩阵 一、矩阵概念的入 矩阵的定义 三、小结 思考题 返

一、矩阵概念的引入 am七1+02x2+.+nxn=b1 1.线性方程组七+02x2+.+2nxn=b, ax+a2x2++ax=b 的解取决于 系数 a,(6,j=1,2,n 常数项b.(i=1,2,n) 上页 返回

       + + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 1. 线性方程组 的解取决于 a (i, j 1,2, ,n), 系数 ij =  b (i , , ,n) 常数项 i = 1 2  一、矩阵概念的引入

线性方程组的系数与常数项按原位置可排为 b, 对线性方程组的 研究可转化为对 这张表的研究. (n2 2.某航空公司在A,B,C,D四 城市之间开辟了若干航线， 如图所示表示了四城市间的 航班图，如果从A到B有航班， 则用带箭头的线连接A与B. 士 页

              n n nn n n n a a a b a a a b a a a b         1 2 21 22 2 2 11 12 1 1 对线性方程组的 研究可转化为对 这张表的研究. 线性方程组的系数与常数项按原位置可排为 2. 某航空公司在A,B,C,D四 城市之间开辟了若干航线 , 如图所示表示了四城市间的 航班图,如果从A到B有航班, 则用带箭头的线连接 A 与B. A B C D

四城市间的航班图情况常用表格来表示： 到站 B D 4 发站 B C D 其中八一表示有航班， 为了便于计算，把表中的改成1，空白地方填上 0,就得到一个数表： 回

四城市间的航班图情况常用表格来表示: 发站 到站 A B C D A B C D 其中 表示有航班. 为了便于计算,把表中的 改成1,空白地方填上 0,就得到一个数表:

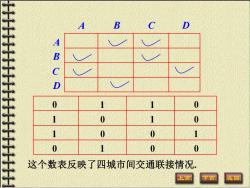
B D A( D 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 这个数表反映了四城市间交通联接情况. 上页

1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 这个数表反映了四城市间交通联接情况. A B C D A B C D

二、矩阵的定义 由m×n个数g(i=1,2,m;j=1,2,.,n) 排成的m行n列的数表 L11 012 L21 L22 Aml am2.amn 称为m×n矩阵.简称m×n矩阵 记作 上页 这回

二、矩阵的定义 由 个数 排成的 行 列的数表 m n m n a (i m j n) ij = 1,2,  , ; = 1,2,  , m m mn n n a a a a a a a a a       1 2 21 22 2 11 12 1 称为 mn 矩阵.简称 m  n 矩阵. 记作

L12 L22 2m 矩阵A的 A= 21 (m,n)元 简记为A=Ann=(n=ag) 这m×n个数称为A的元素，简称为元 元素是实数的矩阵称为实矩阵 元素是复数的矩阵称为复矩阵

              = m m mn n n a a a a a a a a a A        1 1 21 22 2 11 12 1 简记为 ( ) ( ). ij m n A = Am n = aij = a   ( )元 矩阵 的 m n A , 这mn个数称为A的元素,简称为元. 元素是实数的矩阵称为实矩阵, 元素是复数的矩阵称为复矩阵

例如 03 647 是一个2×4实矩阵， 136 21 2 2 是一个3×3复矩阵， 、22 2) 124 是一个3×1矩阵， (2359) (4) 是一个1×4矩阵， 是一个1×1矩阵 回

例如       − 9 6 4 3 1 0 3 5 是一个 24 实矩阵,           2 2 2 2 2 2 13 6 2i 是一个 33 复矩阵,           4 2 1 是一个 31 矩阵, (2 3 5 9) 是一个 14 矩阵, (4) 是一个 11 矩阵

几种特殊矩阵 (1)行数与列数都等于n的矩阵A,称为n阶 方阵.也可记作An 13 6 2i 例如 32 2 2 是一个3阶方阵 22 (2)只有一行的矩阵 A=(a1,2,an) 称为行矩阵（或行向量） 上页

例如           2 2 2 2 2 2 13 6 2i 是一个3 阶方阵. 几种特殊矩阵 (2)只有一行的矩阵 ( , , , ), A = a1 a2  an 称为行矩阵(或行向量). (1)行数与列数都等于 n 的矩阵 A ，称为 n 阶 . 方阵.也可记作 An

只有一列的矩阵 a, B= 称为列矩阵（或列向量）， 不全为0 (3)形如 的方阵，称为对角 矩阵（或对角阵） 回

, 2 1               = an a a B  只有一列的矩阵 称为列矩阵(或列向量). 称为对角 矩阵(或对角阵）.                n          0 0 0 0 0 0 2 1 （3）形如 的方阵, O O 不全为0