《高等数学》课程教学资源（PPT课件）第六章课件_6.2多元函数偏导数及全微分

第六章 第二节 多元画数的偏导数及全微 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第二节 机动 目录 上页 下页 返回 结束 多元函数的偏导数及全微分 第六章

偏导数 偏导数概念及其计算 二、高阶偏导数 HIGH EDUCATION PRESS

偏导数 一、 偏导数概念及其计算 二 、高阶偏导数

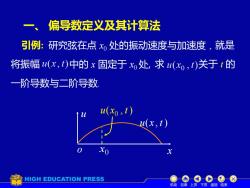
一、 偏导数定义及其计算法 引例：研究弦在点x处的振动速度与加速度，就是 将振幅(x,t)中的x固定于x处，求(xo,t)关于1的 一阶导数与二阶导数 u(x,t) HIGH EDUCATION PRESS 十 机动目录上页下页返回结束

一、 偏导数定义及其计算法 引例: 研究弦在点 x0 处的振动速度与加速度 , 就是 u(x , t ) 0 o x x u 中的 x 固定于 求 一阶导数与二阶导数. x0 处, ( , ) 0 u x t 关于 t 的 机动 目录 上页 下页 返回 结束 将振幅

1.定义1.设函数z=f(x,y)在点(xo,0)的某邻域内 极限 lim f(xo +Ax,Yo)-f(xo>Yo) △x->0 △x 存在，则称此极限为函数z=f(x,y)在点(xo,o)对x 的偏导数，记为 Ox(xo,yo)'a x(00)片2x(w) f(xo,Yo);(o-yo). 注意：人，(x0,%=1m f(x+△x,o)-f(x0,o) △x>0 △x ds f(x d HIGH EDUCATION PRESS eC8 机动目录上页下页返回结束

1.定义1. z = f (x, y) 在点 存在, z f (x, y) 在点(x , y ) 对x = 0 0 的偏导数，记为 ( , ) 0 0 x y 的某邻域内 ; ( , ) 0 0 x x y f   x + x 0 0 x 则称此极限为函数 极限 设函数 f (x0 ) = ( ) ( ) 0 0 f x + x − f x x 0 lim x→ x ; ( , ) 0 0 x x y z d 0 d x x x y = = ( , ) . 1 0 0 f  x y 机动 目录 上页 下页 返回 结束 x f x x y f x y x  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 ( , ) 0 0 f x y 注意 x :

填空题1分 ⊙设置 1.设 sin(xy) xy≠0， f(x,y)= 0, xy=0, 则f(0,1)=[填空1 正常使用填空题需3.0以上版本雨课堂 作答

1.设 则 [填空1] 作答 正常使用填空题需3.0以上版本雨课堂      =  = 0, 0, , 0, sin( ) ( , ) 2 x y x y y x y f x y f x (0,1) = 填空题 1分

同样可定义对y的偏导数 f(xo.)lim f(xo.+)-f(xo-yo) △y>0 △y -jy fGay-n 若函数z=f(x,y)在域D内每一点(x,y)处对x 或y偏导数存在，则该偏导数称为偏导函数，也简称为 偏导数，记为 6z Of Ox'Ox ,x,Jx),x az of ay' Oy ,f,x HIGH EDUCATION PRESS 机动目录上页下页返回结束

同样可定义对 y 的偏导数 lim  →0 = y ( , ) 0 0 f x y y 若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 则该偏导数称为偏导函数, 也简称为 偏导数 , ( , ) , ( , ) 2 f x y f x y y  ( , ) 0 f x ( , ) 0 − f x y 记为 y + y 0 0 y 机动 目录 上页 下页 返回 结束 或 y 偏导数存在 , , , , y z y f y z    

偏导数的概念可以推广到二元以上的函数 例如，三元函数u=f(x,y,)在点(x,y,)处对x的 偏导数定义为 厂(x,yz）)=1im/x+Ax,2)-fx,y,) △x→0 △x f(xy,)=? (请自己写出) f(x,y,)=? HIGH EDUCATION PRESS 机动目录上页下页返回结束

例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 偏导数的概念可以推广到二元以上的函数 . x x + x f (x, y,z) = ? y f (x, y,z) = ? z x 机动 目录 上页 下页 返回 结束 偏导数定义为 (请自己写出)

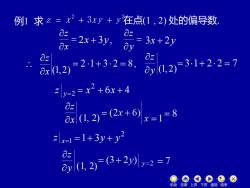
例1求2=x2+3xy+y在点(1,2)处的偏导数 2+3y2 x 2321-32=8 0z 12)31+22=7 2=2=x2+6x+4 03-2+01 x=1=1+3y+y 器262=7 机动目录上页下页返回结束

例1 . 求 2 2 z = x + 3x y + y 解法1: =   x z x (1,2) z    解法2: x (1, 2) z   在点(1 , 2) 处的偏导数. y (1, 2) z   2x + 3y , =   y z 3x + 2y y (1,2) z   6 4 2 = x + x + x=1 z 2 =1+ 3y + y y=2 z 机动 目录 上页 下页 返回 结束 例1 求

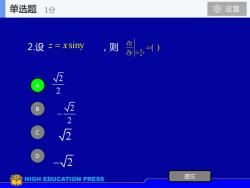
单选题1分 ⊙设置 2.设z=xsiny ,则 2 525 -2 HIGH EDUCATION PRESS 提交

2.设 ，则 A B C D 提交 z x = siny ( ) (1, ) 4 z y   =  2 2 2 2 − 2 − 2 单选题 1分

单选题 2分 ⊙设置 3.设 x-y 则 年(0)0 -2y 2x x-y)2’(x-)7 B 2y 2x (x-y)2'(x-y)2 -2y -2x (x-y)2(x-y)7 2y -2x (x-y)2’(x-y)2 提交

3.设 则 A B C D 提交 x y z x y + = − ( ), ( ) z z x y   = =   2 2 2 2 , ( ) ( ) y x x y x y − − − 2 2 2 2 , ( ) ( ) y x x y x y − − 2 2 2 2 , ( ) ( ) y x x y x y − − − − 2 2 2 2 , ( ) ( ) y x x y x y − − − 单选题 2分