《高等数学》课程教学资源（PPT课件）第五章课件_5-3平面束

第三节 直线及其方程 一、空间直线方程 二、线面间的位置关系 三、平面束 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第三节 一、空间直线方程 二、线面间的位置关系 机动 目录 上页 下页 返回 结束 直线及其方程 三、平面束

空间直线方程 1.一般式方程 直线可视为两平面交线，因此其一般式方程 A1x+By+C12+D1=0 Ax+B2y+C2z+D2=0 (不唯一) HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、空间直线方程 x y z o 0 A1 x + B1 y +C1 z + D1 = 1 2 L 因此其一般式方程 1. 一般式方程 直线可视为两平面交线， (不唯一) 机动 目录 上页 下页 返回 结束

2.对称式方程 已知直线上一点M0(xo,yo,0)和它的方向向量 3=(m,n,p),设直线上的动点为M(x,y,2) 则 MoM//3 M(x,y,2) 故有 x-Xx0_y-Yo 2-20 m n p M(x0,y0,20） 此式称为直线的对称式方程（也称为点向式方程） 说明：某些分母为零时，其分子也理解为零 例如，当m=n=0,p≠0时，直线方程为 x=X0 (y=Yo HIGH EDUCATION PRESS 机动目录上页下页返回结束

( , , ) 0 0 0 0 M x y z 2. 对称式方程 故有 说明: 某些分母为零时, 其分子也理解为零. m x x − 0    = = 0 0 y y x x 设直线上的动点为 则 M (x, y,z) n y y − 0 = p z z − 0 = 此式称为直线的对称式方程(也称为点向式方程) 直线方程为 s 已知直线上一点 ( , , ) 0 0 0 0 M x y z M (x, y,z) 例如, 当 m = n = 0, p  0 时, 和它的方向向量 机动 目录 上页 下页 返回 结束

3.参数式方程 设 x-x0=y-0=2-0=1 m n p 得参数式方程 x=xo+mt y=yo+nt 2=20+pt HIGH EDUCATION PRESS 机动目录上页下页返回结束

3. 参数式方程 设 得参数式方程 : t p z z n y y m x x = − = − = − 0 0 0 x = x + mt 0 y = y + nt 0 z = z + pt 0 机动 目录 上页 下页 返回 结束

例1.求过点A(1,0,1),B的直线方程 HIGH EDUCATION PRESS ○e0C③-8 机动目录上页下页返回结束

例1.求过点 的直线方程 机动 目录 上页 下页 返回 结束

例2.用对称式及参数式表示直线 x+y+z+1=0 2x-y+3z+4=0 解题思路： 先找直线上一点 再找直线的方向向量 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2.用对称式及参数式表示直线 机动 目录 上页 下页 返回 结束 先找直线上一点; 再找直线的方向向量. 解题思路:

二、线面问的位置关系 1.两直线的夹角 两直线的夹角指其方向向量间的夹角（通常取锐角） 设直线L,L,的方向向量分别为 =(m1,h1,1),S2=(m2,n2,p2） 则两直线夹角φ满足 乐 cos O mimz +nn2 +pip2 Vm1+n1+p√m2+n2+p2 HIGH EDUCATION PRESS 机动目录上页下页返回结束

L2 L1  二、线面间的位置关系 1. 两直线的夹角 则两直线夹角  满足 1 2 设直线 L , L = 两直线的夹角指其方向向量间的夹角(通常取锐角) 的方向向量分别为 1 2 1 2 1 2 m m + n n + p p 2 1 2 1 2 m1 + n + p 2 2 2 2 2 m2 + n + p 1 2 1 2 cos s s s  s  = 1 s 2 s 机动 目录 上页 下页 返回 结束

特别有： (1)L11L2→S152→552=0 > mmz +nn2 Pip2 =O (2)Z12→/32×32=0 %1=h=P1 m2 n2 P2 HIGH EDUCATION PRESS 机动目录上页下页返回结束

特别有: 1 2 (1) L ⊥ L 1 2 (2) L // L m1m2 + n1n2 + p1 p2 = 0 2 1 2 1 2 1 p p n n m m = = 1 2 s ⊥ s 1 2 s //s 机动 目录 上页 下页 返回 结束 s1 s2 = 0 s1  s2 = 0

例3.求以下两直线的夹角 -1y_2+3 L: x y+2 z 1-41 2 -2 HIGH EDUCATION PRESS OeOC①8 机动目录上页下页返回结束

例3. 求以下两直线的夹角 2 1 2 2 : 2 − = − + = x y z L 机动 目录 上页 下页 返回 结束

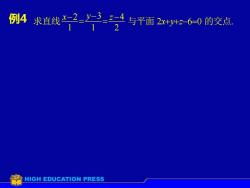
例4求直线=2=3=4与平面2x+4:-6-=0的交点 112 HIGH EDUCATION PRESS

例 例 4 5 求直线 2 4 1 3 1 2 − = − = x− y z 与平面 2x+y+z−6=0 的交点