《高等数学》课程教学资源（PPT课件）第四章课件_4.2一阶微分方程

第二节一阶微分方程 ·一、可分离变量的微分方程 ·二、齐次方程 ·三、一阶线性微分方程

第二节 一阶微分方程 • 一、可分离变量的微分方程 • 二、齐次方程 • 三、一阶线性微分方程

一阶方程的一般形式为F(x》,y)=0 或 =f(x,) d 一阶方程有时也可以写成如下的对称形式 P(K,y)k+Q(x,y)少=0 这个方程虽然简单，也常常很难求出解的 表达式，所以本节只讨论几种特殊类型的一阶微 分方程的解法

一阶方程的一般形式为 F x y y ( , , ) 0  = 或 ( , ) dy f x y dx = 这个方程虽然简单，也常常很难求出解的 表达式, 所以本节只讨论几种特殊类型的一阶微 分方程的解法. 一阶方程有时也可以写成如下的对称形式 P x y dx Q x y dy ( , ) ( , ) 0 + =

一、可分离变量的微分方程 s(y)dy f(x)dx i 可分离变量的微分方程. 例如=2xy→yd=2x2k, dx 这类方程的特点： 经过适当整理，可使方程的一端只含有一个变 量和其微分

g y dy f x dx ( ) ( ) = 可分离变量的微分方程. 5 4 2 2x y dx dy 例如 = 4 5 2 y dy x dx 2 , −  = 这类方程的特点: 经过适当整理，可使方程的一端只含有一个变 量和其微分. 一、可分离变量的微分方程

分离变量方程的解法： g(y)dy=f(x)dx ① 分离变量法 两边积分，得 g()dy-ff()dx G(y) F(x) 则有 G(y)=F(x)+C ② 当G(y)和F(x)可微，且G'(y)=g(y)≠0时，上述过程可逆， 说明由②确定的隐函数y=x)是①的解， 同样F'(x)=f(x)≠0时，由②确定的隐函数x=y) 也是①的解.称②为方程①的隐式通解

当G y F x G y g y ( ) ( ) , ( ) ( ) 0 和 可微 且  =  时， g y y f x x ( )d ( )d = 两边积分, 得 g y y ( )d  = f x x ( )d  ① G y F x C ( ) ( ) = + G y( ) F x( ) ② 说明由②确定的隐函数 y＝(x) 是①的解. 则有 称②为方程①的隐式通解. 上述过程可逆, 由②确定的隐函数 x＝(y) 分离变量法 同样F x f x ( ) ( ) 0 =  时， 分离变量方程的解法: 也是①的解

例1求微分方程少=2y的通解， x 解分离变量 =2xk, y 两端积分∫兜=2，c, Iny=x2+C ∴.y=Ce为所求通解

2 . dy xy dx 例1 求微分方程 = 的通解 解 分离变量 2xdx, y dy = 两端积分 2 , dy xdx y =   2 1 ln | | y x C = + 2 . x  = y Ce 为所求通解

例2求(I+e)y'=e满足yl=0的特解 解方程属于可分离变量的微分方程分离变量，可得 ydy=- +e 积盼： 所以通解为 In()Ca Cla'(. 再由yl=1,得 0=lh2+lnC,即c= 2 故所求特解为 y21Ite' -=In- 2 2

例 2 求(1 e ) ' e x x + = yy 满足 0 | 0 x y = = 的特解. 解 方程属于可分离变量的微分方程. 分离变量, 可得 e d d 1 e x x y y x = + , 积分: e d d 1 e x x y y x = +   , 所以通解为 2 ln(1 e ) ln ln (1 e ) 2 y x x = + + = + C C . 再由 0 | 1 x y = = , 得 0 ln2 ln = + C , 即 1 2 C = . 故所求特解为 2 1 e ln 2 2 x y + =

例3求方程x(1+y2)dx-y(1+x2)dy=0的通解. 解分离变堡1+=1中d 两端积分可1+d 2m1+)=1++nc ln(1+y2)=lnC(1+x2) ∴.1+y2=C1+x2)为方程的通解. 隐式通解

例3 求方程 (1 )d (1 )d 0 的通解. 2 2 x + y x − y + x y = 解 分离变量 x x x y y y d 1 d 1 2 2 + = + 两端积分 = +  y y y d 1 2 ln(1 ) 2 1 ln(1 ) 2 1 2 2 + y = + x ln(1 ) ln (1 ) 2 2 + y = C + x 1 (1 ) 2 2  + y = C + x 为方程的通解. lnC 2 1 + 隐式通解  + x x x d 1 2

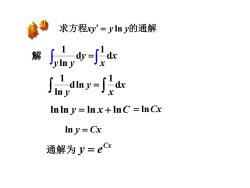
求方程y'=ylny的通解 解 , idoy=-可kae InIn y Inx+InC =InCx Iny=Cx 通解为y=eax

解 x x y y y d 1 d ln 1 =     = x x y y d 1 dln ln 1 lnln y = ln x + lnC = lnCx ln y = Cx Cx 通解为 y = e 求方程xy y y  = ln 的通解

二、齐次方程 1定义形如血=（占的微分方程称为齐次方程。 dx 例如：（y-y2)=(x2-2y)d y-心2 可化为： 迎=y-y2 dx x2-2xy 即： 1-2) dx 2.解法 作变量代换u=y,即y=xm, 义=u+ du

二、齐次方程 2 2 例如： ( ) ( 2 ) xy y dx x xy dy − = − 2 2 2 dy xy y dx x xy − = − 可化为： ( ) dy y dx x 形如 =  的微分方程称为齐次方程. 2.解法 , y u x 作变量代换 = 即 y xu = , , dy du u x dx dx  = + 1.定义 2 ( ) 1 2( ) y y dy x x dx y x − = − 即：

du 代入原式 u+x =p(W), dx 即 du p(u)-u 可分离变量的方程 d X 分离变量得： du c P(u)-u 两端积分得： 得」

, ( ) du dx  u u x = − 得   代入原式 ( ), du u x u dx + =  ( ) . du u u dx x  − 即 = 可分离变量的方程 分离变量得： ( ) du dx  u u x = − 两端积分得：