《高等数学》课程教学资源（书籍教材）第五章向量与空间解析几何

同济大学数学系列教材 高等数学 下附 八7 人民邮电出版社 北京

同济大学数学系列教材 吉刍米 向寸女女子严 下 册 同济大学数学系 编 人民邮电出版社 北 京 人民邮电出版社

内容提要 本书品按照数育部大学数学惧程数学指导秀品会的堪本愿求，充分吸取当前优秀高等数学教材的结 华，并结合同济大学数学系多年来的教学实践经验，针对当前学生的知识结构和习惯特点而编写的。全 书分为上、下两册。本书为下册，是多元函数微积分部分，共四意，主要内容包括向量与空间解析几何 多元函数微分学，多元函数积分学，无穷级数。每节前面配有课前导读，核心知识点配备微课，每章后 面附有竞节测试和拓展阅读。 本书注重知识点的引入方法，使之符合认知规律，更易于读者接受。同时，本书精炼了主要内容， 对部分内容调整了顺序，使结构更加简洁，思路更加清嘶。本书还注重知识的连贯性，例题的多样性和 习题的丰富性、层次性，使读者在学习数学知识点的同时拓宽祝野，欣赏数学之美。 民邮电出版 本书可作为高等院校理工科类各专业的教材，也可作为社会从业人员的自学参考用 ◆编 同济大学数学系 责任编辑许金霞 责任印制沈蓉 人民邮电出版社出版发行 北京市丰台区成寿寺路写 电了郎价 315@ptpress.com.cr w.p 北京 印制 ◆开本：787x1092V16 印张：18 2016年月第1版 字数： 千亨 2016年月北京第1次印削 定价： 元 读者服务热线：(010)8105256印装质量热线：(010)81055316

人民邮电出版社

日 录 第五章向量与空间解析何.1 第六章多元函数微分学.53 第一节向量及其运算 第一节多元函数的概念、极限与 一、空间直角坐标系 连续.53 二、向量的运算 .3 一、平面上的集合.53 三、向量的模、方向角.7 二、二元函数的概念.54 四、数量积4.9 三、二元函数的极限.56 五、向量积 .12 四、 二元函数的连续性 .57 大、混合积.14 习陌6- .59 习题5-1 .16 第二节多元函数的偏导数与 第二节平面及其方程.18 全微分.60 一、平面的点法式方程.18 、偏导数.60 二、平面的一般方程.20 三全微分 66 三、平面的截距式方程.2 。习瓶6-2.70 四、平面与平面、点与平面的关系 21人V第三节 复合求导、隐函数求导及 习题5-2.23 方向导数.72 第三节直线及其方程 2%24 一、多元函数复合求导 .73 一、空间直线一般方程.25 二、隐函数的求导公式.79 二、对称式方程及参数方程小.25 三、方向导数与棉度.85 三、直线与平面的关系.27 习期6-3.90 四、平面束.29 第四节多元函数微分学的应用+.93 习题5-3 .30 空间曲线的切线与法平面 .93 第四节曲面与曲线.32 二、空间曲面的切平面与法线.100 一、曲面方程的概念.33 三、多元函数的极值 .103 二旋转曲面. 434 习瓶6-4. .108 三、柱面.36 本章小结.111 四、二次曲面.37 章节测试六.113 五、空间曲线及其方程.40 拓展阅读.115 六、空间曲线在坐标面上的投影 42 第七章多元函数积分学.119 习题5-4.44 本章小结. 46 第一节二重积分的概念、计算和 章节测试五.47 应用.119 拓展阅读.49 二重积分的概念和性质.119 1

人民邮电出版社

目录 二、直角坐标系下二重积分的计算.122 习瓶7-5.203 三、极坐标系下二重积分的计算.130 本章小结.208 四、一重积分换元法.·134 章节测试七.209 五、二重积分应用举例. 36 拓展阅读 .211 习题7-1.142 第二节三重积分的概念、计算和 第八章无穷级数 215 应用 .146 第一节常数项级数的概念与 一三重积分的概令.146 性质.215 二、三重积分的计算 .147 常数项级数的概念.215 三、三重积分的应用 二，收敛级数的基本性质.219 习题7-2.153 习题8-1.221 第三节对弧长的曲线积分与对坐标 第二节常数项级数的审敛准则.223 的曲线积分。155 一、正项级数及其审敛性.224 一、对狐长的曲线积分（第一类 交错级数及其审敛性.23 曲线积分).155 三、绝对收敛和条件收敛.232 二、对坐标的曲线积分（第二类 习题8-2. .234 曲线积分) .161 第三节幂级数的收敛及函数的 习题7-3. .169 展开式.238 第四节对面积的曲面积分与对坐标 函数项级数的慨念.238 的曲面积分.17 二、幂级数及其收敛性.239 。对面积的曲面积分（第一类 三、函数展开成幂级数 .247 曲面积分).2172 习题8-3.25 二、对坐标的曲面积分（第类 第四节傅里叶级数.253 曲面积分)心.177 、周期为2x的函数的傅里叶 习题7-4.小.186 级数.253 第五节格林公式、高斯公式和 、一般周期函数的傅里叶级数.260 斯托克斯公式.188 习酒8-4.26 一、格林公式及其应用.188 本章小结.263 二、高斯公式、通量与散度.197 章节测试八.265 ·三、斯托克斯公式、环流量与 拓展阅读 .267 旋度.201 习题答案 269 2

人民邮电出版社

第五章向量与空间解析几何 第一节向量及其运算 [课前导读] 既有大小又有方向的物理量称为向量在数学上可用有向线段来表示向量，其长度表 示向量的大小，其方向（箭头）表示向量的方向 (1)向量的表示：以M,为起点、M2为终点的有向线段表示的向量记为M,M,有时也 用一个黑体字母（书写时，在字母上面加一箭头）来表示（见图5-），/如a或 a 图5-1 (2)向量的模：向量的大小（数学上指有向线段的长度）叫作向量的模，记作| |M,1,模为1的向量称为单位向量（见图5-1），记作e.模为0的向量称为零向量，记 作0.零向量的方向可以看作是任意的。 (3)向径：以原点0为始点，向一点M引向量0丽，这个向量叫作点M对于点0的向 径，记作r,即r=O (4)自由向量：只与大小、方向有关，而与起点处无关的向量称为自由向量 一、空间直角坐标系 过空间一个定点0，作三条互相垂直且具有相同的长度单位的数轴（见图5-2），这三 条数轴分别称为x轴（横轴）、y轴（纵轴）、：轴（竖轴），统称坐标轴，定点O称为原点，其 正向符合右手规则（见图5-3）.这样的三条坐标轴就组成了空间直角坐标系。 三条坐标轴中的两条可确定一个平面，即xOy、yOz、Ox平面，统称坐标面.它们把 空间分成了八个卦限，在xO平面上面逆时针依次为I、Ⅱ、Ⅲ、V卦限，下面依次为 V、M、Ⅷ卦限，如图5-4所示. .1

人民邮电出版社

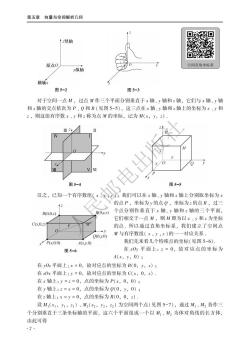
第五章向量与空间解析几何 竖轴 原点0 纵轴 空问直角坐标系 横轴 图5-2 图5-3 对于空间一点M,过点M作三个平面分别垂直于x轴、y轴和：轴，它们与x轴、y轴 和：轴的交点依次为P、Q和R(见图5-5)，这三点在x轴、y轴和：轴上的坐标为x、y和 :,则这组有序数x、y和：称为点M的坐标，记为M(x,y,)· 图5-5 反之，已知一个有序数组(x,我们可以在x轴、y轴和：轴上分别取坐标为 的点P,坐标为y的点Q,坐标为z的点R,过 12 R0.0, B0.） 个点分别作垂直于x轴、y轴和：轴的三个平面 它们相交于一点M,则M即为以x、y和：为坐标 Cx.0.=) 的点，所以通过直角坐标系，我们建立了空间点 Q00) M与有序数组(x,y,z)的一一对应关系. Px0,0) M(xv:0) 我们先来看几个特殊点的坐标（见图5-6）. 图5-6 在xOy平面上：：=0，故对应点的坐标为 A(x,y,0); 在yO:平面上：x=0,故对应点的坐标为B(0,y,z); 在z0x平面上：y=0,故对应点的坐标为C(x,0,) 在x轴上：y=:=0,点的坐标为P(x,0,0): 在y轴上：a=x=0,点的坐标为Q(0,y,0): 在：轴上：x=y=0,点的坐标为R(0,0,). 设M1(x,1,1)、M(x2,2)为空间两个点（见图5-7），通过M1、M2各作三 个分别垂直于三条坐标轴的平面，这六个平面组成一个以M,、M2为体对角线的长方体， 由此可得 2+

人民邮电出版社

第一节向量及其运算 d2=1M1M212=(x2-x1)2+(2-y1)2+(2-41)2, 即 d=M,M1=/(2-x)2+(2-y)2+(2-)2. 例1证明以点M1(4,3,1)、M2(7,1,2)及 M(5,2,3)为顶点的三角形是等腰三角形. 证1MM1=√(7-4)2+(1-3)2+(2-1) =14, 1M2M1=(5-7)2+(2-1)2+(3-2) 图5-7 =6, 1MM1=√(4-5)2+(3-2)2+(1-3)2=√6 即|M2=MM1,因此该三角形是等腰三角形。 例2在z轴上求与两点A(-4,1,7)和B(3,5,-2)等距离的点 解设所求点的坐标为M(0,0,),由A=B即 0+42+(0-)2+(-7=3-05702+(-2-, 得：14 14. ,因此所求点的坐标为M(0,0, 9· 二、向量的运算 1.向量的投影及投影定理 将非零向量α、b的始点重合，在两向量的所在平面上，若一个向量逆时针方向转过 角度0后可与另一个向量正向重合（见图5-8），则称0为向 量a、b的夹角，记作(a,b),即 0=(a,b)=(b,a)(0≤0≤m). 对于向量a、b,如果它们的夹角=0或=,则称 这两个向量平行，记为a/b,其中两个向量指向一致时 6=0,指向相反时0=T.指向相同的两个平行向量a、b如 果还满足a=b,那么这两个向量相等，记为a=b.与向 图5-8 量a的模相同，但方向相反的向量叫作a的负向量，记作-a 对于一向量与一轴的夹角，可将其中一轴看作向量 按两向量之间的夹角来度量：对于两个轴之间的夹角，则看作两向量的夹角. 通过空间一点A作与u轴垂直的平面（见图5-9），该平面与u轴的交点A'称为点A在 u轴上的投影 如果向量AB的始点A与终点B在u轴上的投影分别为A'、B(见图5-10)，则u轴上 的有向线段A'B的值A'B'称为向量A店在u轴上的投影，记作P.AB=A'B',u轴称为投 影轴. 3

人民邮电出版社

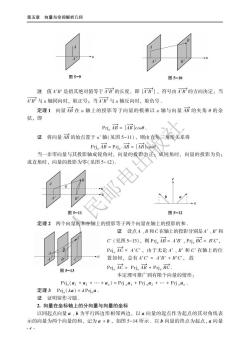
第五章向量与空间解析几何 图5-9 图5-10 注值A'B是指其绝对值等于A'B的长度，即|A'B1,符号由A'B的方向决定：当 AB与u轴同向时，取正号：当B与u轴反向时，取负号 定理1向量AB在u轴上的投影等于向量的模乘以u轴与向量AB的夹角0的余 弦，即 Pri.AB=AB cos0. 证将向量A店的始点置于4轴（见图5-11），则由直角三角形关系得 Pri.AB Pri AB=AB cose. 当一非零向量与其投影轴成锐角时，向量的投影为正成钝角时，向量的投影为负： 成直角时，向量的投影为零（见图5-12）. 图5-11 图5-12 定理2两个向量的和在轴上的投影等于两个向量在轴上的投影的和. 证设点A、B和C在轴上的投影分别是'、B'和 C(见图5-13)，则Pj.A店=A'B',P可j.B元=B'C Prj,AC=A'C',由于无论A'、B'和C'在轴上的位 置如何，总有A'C=A'B'+B'C',故 图5-13 Prj.AC Prj.AB Prj.BC 本定理可推广到有限个向量的情形： Prj(a1+a2+.+an)=P可ja1+Pja2+.+Pjan 定理3Prj,(Aa)=APrja 证证明留作习题. 2.向量在坐标轴上的分向量与向量的坐标 以同起点向量a、b为平行四边形相邻两边，以a向量的起点作为起点的其对角线表 示的向量为两个向量的和，记为a+b,如图5-14所示，以b向量的终点为起点，a向量 4

人民邮电出版社

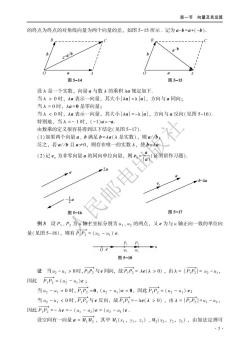
第一节向量及其运算 的终点为终点的对角线向量为两个向量的差，如图5-15所示，记为a-b=a+(-b) c-atb 图5-14 图5-15 设入是一个实数，向量a与数A的乘积a规定如下. 当A>0时，Aa表示一向量，其大小Aa=入al,方向与a同向： 当A=0时，Aa=0是零向量； 当A0时，P与e同向，故P,P=A(A>0),由A=1PP=2-4, 因此P,P=(山2-)e； 当42-41=0时，PP=0,(2-u1)e=0,因此PD=(42-41)e: 当42-410),由入=|PP1=41-42 因此P乃=-Ae=-(u1-)e=(u-4)e 设空间有一向量a=MM,其中M,(x1,)、M2(x2,2,2),由加法定理可 ,5

人民邮电出版社

第五章向量与空间解析几何 知a可分解为三个分别平行于x轴、y轴和z轴的向量ax、a,和a,它们称为a在x轴、y 轴和：轴的三个分向量.显然a=a,+a,+a,(见图5-19) 图5-19 设-1=a,-=a,-41=4,则有 Prj,a=Prj,a,=x2-xa Prj,a Prj,a,=y2, Prja =Prj.a:=a. 若用i、方和k分别表示与x轴、y轴和轴正向一致的三个单位向量，称它们为基本单 位向量，则有a,=(-i,a,发1，a,=(-k,因此 a=a,+a,+a,=(x2x1)it2-y1)j+(2-1)k=a,i+aj+a,k, 称上式为向量a按甚本单位向量的分解式或a的向量表示式， 一方面，从向量a可以唯二定出它在三条坐标轴上的投影a,、a,和a:,另一方面， 从a、a,和a,可以唯定出向量a,这样有序数组a,、a,、a,就与向量a一一对应，于是 将a,、a,、a,称为向量a的坐标，记为a=(a,a,a),也称为向量a的坐标表示式 以M,(x1,1)为始点、M2(2,y2,2)为终点的向量记为 M1M=(x2-x1,y2-1,32-）· 特别地，M(x,y,z),向径r=0O7=(x,y,z)(见图 5-20) 对于向量的运算也可化为对坐标的数量运算。 设向量a=(a,a,a,),b=(b,b,b),则 a±b=(a,i+a,j+a.k)±(b,i+b,j+bk) =(a±b,)i+(a,±b,j+(a±b)k =(a,±bx,ay±b,a±b); Aa=A(a,i+a,j+ak)=(Aa,)i+(Aa,)j+(Aa.)k= (Aax,Aa,Aa）. 图5-20 例4设A(x1,1,)和B(x2,y2,2)为空间两

人民邮电出版社