《管理运筹学》课程教学课件（PPT讲稿）第2章 线性规划与单纯形法

第二章 线性规划与单纯形法 §1 线性规划问题的提出及其数学模型 §2 图解法及单纯型法解题思路 §3“管理运筹学”软件的操作方法 。 §4人力资源分配的问题 §5 套裁下料问题 §6 配料问题 §7 投资问题

管 理 运 筹 学 1 第二章 线性规划与单纯形法 • §1 线性规划问题的提出及其数学模型 • §2 图解法及单纯型法解题思路 • §3 “管理运筹学”软件的操作方法 • §4 人力资源分配的问题 • §5 套裁下料问题 • §6 配料问题 • §7 投资问题

§1线性规划问题的提出及其数学模型 在管理中一些典型的线性规划应用 ·合理利用线材问题：如何在保证生产的条件下，下料最少 ·配料问题：在原料供应量的限制下如何获取最大利润 ·投资问题：从投资项目中选取方案，使投资回报最大 ·产品生产计划：合理利用人力、物力、财力等，使获利最 大 劳动力安排：用最少的劳动力来满足工作的需要 ·运输问题：如何制定调运方案，使总运费最小

管 理 运 筹 学 2 在管理中一些典型的线性规划应用 • 合理利用线材问题：如何在保证生产的条件下，下料最少 • 配料问题：在原料供应量的限制下如何获取最大利润 • 投资问题：从投资项目中选取方案，使投资回报最大 • 产品生产计划：合理利用人力、物力、财力等，使获利最 大 • 劳动力安排：用最少的劳动力来满足工作的需要 • 运输问题：如何制定调运方案，使总运费最小 §1 线性规划问题的提出及其数学模型

§1线性规划问题的提出及其数学模型 例1.某工厂在计划期内要安排I、Ⅱ两种产品的生 产，已知生产单位产品所需的设备台时及A、B两 种原材料的消耗、资源的限制，如下表： I 资源限制 设备 1 1 300台时 原料A 2 1 400千克 原料B 0 1 250千克 单位产品获利 50元 100元 问题：工厂应分别生产多少单位I、Ⅱ产品才能使 工厂获利最多？ 3

管 理 运 筹 学 3 §1 线性规划问题的提出及其数学模型 例1. 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生 产，已知生产单位产品所需的设备台时及A、B两 种原材料的消耗、资源的限制，如下表： 问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使 工厂获利最多？ Ⅰ Ⅱ 资源限制 设备 1 1 300 台时 原料 A 2 1 400 千克 原料 B 0 1 250 千克 单位产品获利 50 元 100 元

§1线性规划问题的提出及其数学模型 线性规划模型： 决策变量：x1:I产品的产量，x2:IⅡ产品的产量 目标函数：Max z=50x1+100x2 约束条件： s.t. x1+ X2≤ 300 2x1+ x2 ≤400 X2≤ 250 x1, x2 ≥0 备 4

管 理 运 筹 学 4 §1 线性规划问题的提出及其数学模型 • 线性规划模型： 决策变量： x1：Ⅰ产品的产量， x2：Ⅱ产品的产量 目标函数：Max z = 50 x1 + 100 x2 约束条件： s.t. x1 + x2 ≤ 300 2 x1 + x2 ≤ 400 x2 ≤ 250 x1 , x2 ≥ 0

§1线性规划问题的提出及其数学模型 例2某公司由于生产需要，共需要A,B两种原料至少350 吨(A,B两种材料有一定替代性)，其中A原料至少购进125 吨。但由于A,B两种原料的规格不同，各自所需的加工时间 也是不同的，加工每吨A原料需要2个小时，加工每吨B原料需 要1小时，而公司总共有600个加工小时。又知道每吨A原料的 价格为2万元，每吨B原料的价格为3万元，试问在满足生产需 要的前提下，在公司加工能力的范围内，如何购买A,B两种 原料，使得购进成本最低？ 5

管 理 运 筹 学 5 §1 线性规划问题的提出及其数学模型 例2 某公司由于生产需要，共需要A，B两种原料至少350 吨（A，B两种材料有一定替代性），其中A原料至少购进125 吨。但由于A，B两种原料的规格不同，各自所需的加工时间 也是不同的，加工每吨A原料需要2个小时，加工每吨B原料需 要1小时，而公司总共有600个加工小时。又知道每吨A原料的 价格为2万元，每吨B原料的价格为3万元，试问在满足生产需 要的前提下，在公司加工能力的范围内，如何购买A，B两种 原料，使得购进成本最低？

§1线性规划问题的提出及其数学模型 决策变量：x1,原料A的购买量，x2:原料B购买量 目标函数： Min f=2x+3x2 约束条件： s.t. X1+X2≥350 Xj ≥125 2X1+X2≤600 X1,X2≥0 6

管 理 运 筹 学 6 §1 线性规划问题的提出及其数学模型 决策变量： x1：原料A的购买量，x2：原料B购买量 目标函数： Min f = 2x1 + 3 x2 约束条件： s.t. x1 + x2 ≥ 350 x1 ≥ 125 2 x1 + x2 ≤ 600 x1 , x2 ≥ 0

§1线性规划问题的提出及其数学模型 建模过程 1.理解要解决的问题，了解解题的目标和条件： 2定义决策变量(X1,X2,x)，每一组值表 示一个方案； 3.用决策变量的线性函数形式写出目标函数，确定最 大化或最小化目标； 4.用一组决策变量的等式或不等式表示解决问题过程 中必须遵循的约束条件

管 理 运 筹 学 7 §1 线性规划问题的提出及其数学模型 • 建模过程 1.理解要解决的问题，了解解题的目标和条件； 2.定义决策变量（ x1 ，x2 ，. ，xn ），每一组值表 示一个方案； 3.用决策变量的线性函数形式写出目标函数，确定最 大化或最小化目标； 4.用一组决策变量的等式或不等式表示解决问题过程 中必须遵循的约束条件

§1线性规划问题的提出及其数学模型 一般形式 决策变量设置： X1,X2,.’X 目标函数： Max (Min)Z=c1x1+c2 x2+.Cn Xn 约束条件： s.t. ++至8 amlX1+am2X2+.+amnX≤（=，≥）bm X1’X2,.,X≥0

管 理 运 筹 学 8 §1 线性规划问题的提出及其数学模型 • 一般形式 决策变量设置： x1， x2， . ， xn 目标函数： Max （Min） z = c1 x1 + c2 x2 + . + cn xn 约束条件： s.t. a11 x1 + a12 x2 + . + a1n xn ≤ （ =, ≥ ）b1 a21 x1 + a22 x2 + . + a2n xn ≤ （ =, ≥ ）b2 . . am1 x1 + am2 x2 + . + amn xn ≤ （ =, ≥ ）bm x1 ，x2 ，. ，xn ≥ 0

§2图解法及单纯型法解题思路 对于只有两个决 例1.目标函数： 策变量的线性规划问 Max z=50X1+100x2 题，可以在平面直角 约束条件： 坐标系上作图表示线 s.t. 性规划问题的有关概 X1+ X2≤300 (A) 2X1+ X≤ 400 (B) 念，并求解。 X≤250 (C) 下面通过例1详细 X1≥0 (D) 2≥0 (E) 讲解其方法： 得到最优解： X1=50, X2=250 最优目标值z=27500 9

管 理 运 筹 学 9 例1.目标函数： Max z = 50 x1 + 100 x2 约束条件： s.t. x1 + x2 ≤ 300 (A) 2 x1 + x2 ≤ 400 (B) x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E) 得到最优解： x1 = 50， x2 = 250 最优目标值 z = 27500 §2 图解法及单纯型法解题思路 对于只有两个决 策变量的线性规划问 题，可以在平面直角 坐标系上作图表示线 性规划问题的有关概 念，并求解。 下面通过例1详细 讲解其方法：

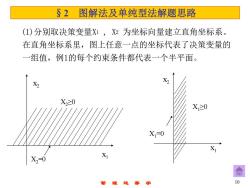
§2图解法及单纯型法解题思路 (1)分别取决策变量X1，X2为坐标向量建立直角坐标系。 在直角坐标系里，图上任意一点的坐标代表了决策变量的 一组值，例1的每个约束条件都代表一个半平面。 X X2≥0 X1≥0 X=0 X X2=0 X 10

管 理 运 筹 学 10 §2 图解法及单纯型法解题思路 (1)分别取决策变量X1 , X2 为坐标向量建立直角坐标系。 在直角坐标系里，图上任意一点的坐标代表了决策变量的 一组值，例1的每个约束条件都代表一个半平面。 x2 x1 X2≥0 X2=0 x2 x1 X1≥0 X1=0