《管理运筹学》课程教学课件（PPT讲稿）第4章 整数线性规划

第四章 整数线性规划 §1整数线性规划的图解法 §2整数线性规划的计算机求解 §3整数线性规划的应用

管 理 运 筹 学 1 第四章 整数线性规划 §1 整数线性规划的图解法 §2 整数线性规划的计算机求解 §3 整数线性规划的应用

§1 整数规划的图解法 例1.某公司拟用集装箱托运甲、乙两种货物，这两种货物每件的体积、 重量、可获利润以及托运所受限制如表所示。 货物 每件体积 每件重量 每件利润 (立方英尺) (百千克) (百元) 甲 195 4 2 乙 273 40 3 托运限制 1365 140 甲种货物至多托运4件，问两种货物各托运多少件，可使获得利润最大。 解：设x1、x2分别为甲、乙两种货物托运的件数，建立模型 目标函数：Maxz=2X1+32 约束条件：s.t 195x1+273x2≤1365 4x1+40x2≤140 X1≤4 x1,2≥0为整数。 如果去掉最后一个约束，就是一个线性规划问题。利用图解法， 曹建运筹学

管 理 运 筹 学 2 §1 整数规划的图解法 例1. 某公司拟用集装箱托运甲、乙两种货物，这两种货物每件的体积、 重量、可获利润以及托运所受限制如表所示。 甲种货物至多托运4件，问两种货物各托运多少件，可使获得利润最大。 解：设x1 、x2分别为甲、乙两种货物托运的件数，建立模型 目标函数： Max z = 2x1 +3 x2 约束条件： s.t. 195 x1 + 273 x2 ≤1365 4 x1 + 40 x2 ≤140 x1 ≤4 x1，x2 ≥ 0 为整数。 如果去掉最后一个约束，就是一个线性规划问题。利用图解法， 货物 每件体积 （立方英尺） 每件重量 （百千克） 每件利润 （百元） 甲 乙 195 273 4 40 2 3 托运限制 1365 140

第五章 整数线性规划 整数规划一类要求问题的解中的全部或一部 分变量为整数的数学规划。从约束条件的构 成又可细分为线性，二次和非线性的整数规 划。 。 求整数解的线性规划问题，不是用四舍五入 法或去尾法对线性规划的非整数解加以处理 都能解决的，而要用整数规划的方法加以解 决

管 理 运 筹 学 3 第五章 整数线性规划 • 整数规划一类要求问题的解中的全部或一部 分变量为整数的数学规划。从约束条件的构 成又可细分为线性，二次和非线性的整数规 划。 • 求整数解的线性规划问题，不是用四舍五入 法或去尾法对线性规划的非整数解加以处理 都能解决的，而要用整数规划的方法加以解 决

第五章 整数线性规划 在整数规划中，如果所有的变量都为整数，则称为 纯整数规划问题；如果有一部分变量为整数，则称 之为混合整数规划问题。在整数规划中，如果变量 的取值只限于0和1，这样的变量我们称之为0-1变 量。如果所有的变量都为0-1变量，则称之为0-1规 划。 0-1变量可以数量化地描述诸如开与关、取与弃、 有与无等现象所反映的离散变量间的逻辑关系、顺 序关系以及互斥的约束条件，因此0-1规划非常适 合描述和解决如线路设计、工厂选址、生产计划 安排、旅行购物、背包问题、人员安排、代码选取、 可靠性等人们所关心的多种问题。实际上，凡是有 界变量的整数规划都可以转化为0-1规划来处理

管 理 运 筹 学 4 第五章 整数线性规划 • 在整数规划中，如果所有的变量都为整数，则称为 纯整数规划问题；如果有一部分变量为整数，则称 之为混合整数规划问题。在整数规划中，如果变量 的取值只限于0和1，这样的变量我们称之为0-1变 量。如果所有的变量都为0-1变量，则称之为0-1规 划。 • 0-1变量可以数量化地描述诸如开与关、取与弃、 有与无等现象所反映的离散变量间的逻辑关系、顺 序关系以及互斥的约束条件 ，因此0-1规划非常适 合描述和解决如线路设计 、工厂选址 、生产计划 安排、旅行购物、背包问题、人员安排、代码选取、 可靠性等人们所关心的多种问题。实际上，凡是有 界变量的整数规划都可以转 化为0-1规划来处理

§1 整数线性规划的图解法 3 2x1+3x2=14.66 2 2x1+3x2=14 22x+3=6 3 4 得到线性规划的最优解为x1=2.44,X2=3.26,目标函数值为14.66。 由图表可看出，整数规划的最优解为x=4,X2=2,目标函数值为14。 性质1：任何求最大日标函数值的纯整数规划或混合整数规划的最大目 标函数值小于或等于相应的线性规划的最大目标函数值；任何求最小目 标函数值的纯整数规划或混合整数规划的最小目标函数值大于或等于相 应的线性规划的最小目标函数值

管 理 运 筹 学 5 得到线性规划的最优解为x1=2.44, x2=3.26,目标函数值为14.66。 由图表可看出，整数规划的最优解为x1=4, x2=2,目标函数值为14。 性质1：任何求最大目标函数值的纯整数规划或混合整数规划的最大目 标函数值小于或等于相应的线性规划的最大目标函数值；任何求最小目 标函数值的纯整数规划或混合整数规划的最小目标函数值大于或等于相 应的线性规划的最小目标函数值。 1 2 3 4 1 2 3 2x1+3x2 =14.66 x1 x2 2x1+3x2 =14 2x1+3x2 =6 §1§1 整数线性规划的图解法 整数规划的图解法

§2 整数线性规划的计算机求解 例2： 例3： Max Z=3X+2+3X3 Max Z 3x1+x2 3x3 s.t. s.t. -X1+2为+X3≤4 -X1+2x2+X3≤4 42-3x≤2 4x2-3x3≤2 ≤3 为-32+2为≤3 X1-3x2+2x3 Xg≤1 X1,X2,为≥0 为整数 X1,X2,X3≥0 X1, 3为整数 X3为 0-1变量 用《管理运筹学》软件求解得： 用《管理运筹学》软件求解得： 为兰5为=2为=2 五=42=1.253=1 z=16.25 学 6

管 理 运 筹 学 6 例2： Max z = 3x1 + x2 + 3x3 s.t. -x1 + 2x2 + x3 ≤ 4 4x2 -3x3 ≤2 x1 -3x2 + 2x3 ≤3 x1,x2,x3 ≥ 0 为整数 例3： Max z = 3x1 + x2 + 3x3 s.t. -x1 + 2x2 + x3 ≤ 4 4x2 -3x3 ≤2 x1 -3x2 + 2x3 ≤3 x3 ≤1 x1,x2,x3 ≥ 0 x1，x3 为整数 x3 为 0-1变量 用《管理运筹学》软件求解得： x1 = 5 x2 = 2 x3 = 2 用《管理运筹学》软件求解得： x1 = 4 x2 = 1.25 x3 = 1 z = 16.25 §2 整数线性规划的计算机求解

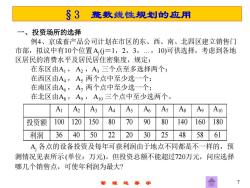
§3整数线性规划的应用 一、投资场所的选择 例4、京成畜产品公司计划在市区的东、西、南、北四区建立销售门 市部，拟议中有10个位置AG=1,2,3,.,10)可供选择，考虑到各地 区居民的消费水平及居民居住密集度，规定： 在东区由A1,A2,A3三个点至多选择两个： 在西区由A4,A两个点中至少选一个； 在南区由A,A,两个点中至少选一个： 在北区由Ag, Ag, A0三个点中至少选两个。 A A2 A3 A4 As A6 A1 As Ag A10 投资额 100 120 150 80 70 90 80 140 160 180 利润 36 40 50 22 20 30 25 48 58 61 A各点的设备投资及每年可获利润由于地点不同都是不一样的，预 测情况见表所示（单位：万元）。但投资总额不能超过720万元，问应选择 哪几个销售点，可使年利润为最大？

管 理 运 筹 学 7 §3 整数线性规划的应用 一、投资场所的选择 例4、京成畜产品公司计划在市区的东、西、南、北四区建立销售门 市部，拟议中有10个位置Aj (j＝1，2，3，.，10)可供选择，考虑到各地 区居民的消费水平及居民居住密集度，规定： 在东区由A1 ， A2 ，A3 三个点至多选择两个； 在西区由A4 ， A5 两个点中至少选一个； 在南区由A6 ， A7 两个点中至少选一个； 在北区由A8 ， A9 ， A10 三个点中至少选两个。 Aj 各点的设备投资及每年可获利润由于地点不同都是不一样的，预 测情况见表所示(单位：万元)。但投资总额不能超过720万元，问应选择 哪几个销售点，可使年利润为最大? A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 投资额 100 120 150 80 70 90 80 140 160 180 利润 36 40 50 22 20 30 25 48 58 61

§3 整数线性规划的应用 解：设：0-1变量x,=1(A点被选用)或0(A点没被选用)。 这样我们可建立如下的数学模型： Maxz=36x1+40+50x3+22x4+20x5+30x6+25x7+48g+58xg+61x10 s.t.100x+1202+1503+80x4+70x5+90x6+80x+140g+160xg+180x10 ≤720 X1+X2十X3 ≤2 X4+X5 ≥1 X6十X7 ≥1 X8+X9+为10≥2 x≥0且x为0-1变量，i=1,2,3,10 8

管 理 运 筹 学 8 §3 整数线性规划的应用 解：设：0-1变量 xi = 1 (Ai 点被选用）或 0 (Ai 点没被选用）。 这样我们可建立如下的数学模型： Max z =36x1+40x2+50x3+22x4+20x5+30x6+25x7+48x8+58x9+61x10 s.t. 100x1+120x2+150x3+80x4+70x5+90x6+80x7+140x8+160x9+180x10 ≤ 720 x1 + x2 + x3 ≤ 2 x4 + x5 ≥ 1 x6 + x7 ≥ 1 x8 + x9 + x10 ≥ 2 xj ≥ 0 且xj 为0-1变量，i = 1,2,3,.,10

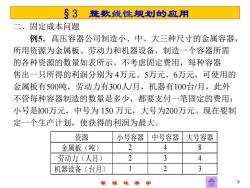
§3数线性规划的应用 二、 固定成本问题 例5.高压容器公司制造小、中、大三种尺寸的金属容器， 所用资源为金属板、劳动力和机器设备，制造一个容器所需 的各种资源的数量如表所示。不考虑固定费用，每种容器 售出一只所得的利润分别为4万元、5万元、6万元，可使用的 金属板有500吨，劳动力有300人/月，机器有100台/月，此外 不管每种容器制造的数量是多少，都要支付一笔固定的费用： 小号是100万元，中号为150万元，大号为200万元。现在要制 定一个生产计划，使获得的利润为最大。 资源 小号容器 中号容器 大号容器 金属板（吨） 2 4 8 劳动力（人月） 2 3 4 机器设备（台月)》 1 2 3 理运筹学

管 理 运 筹 学 9 §3 整数线性规划的应用 二、固定成本问题 例5．高压容器公司制造小、中、大三种尺寸的金属容器， 所用资源为金属板、劳动力和机器设备，制造一个容器所需 的各种资源的数量如表所示。不考虑固定费用，每种容器 售出一只所得的利润分别为 4万元、5万元、6万元，可使用的 金属板有500吨，劳动力有300人/月，机器有100台/月，此外 不管每种容器制造的数量是多少，都要支付一笔固定的费用： 小号是l00万元，中号为 150 万元，大号为200万元。现在要制 定一个生产计划，使获得的利润为最大。 资源 小号容器 中号容器 大号容器 金属板（吨） 2 4 8 劳动力（人月） 2 3 4 机器设备（台月） 1 2 3

§3 整数线性规划的应用 解：这是一个整数规划的问题。 设x1,x2,x3分别为小号容器、中号容器和大号容器的生产数量。 各种容器的固定费用只有在生产该种容器时才投入，为了说明固定费用 的这种性质，设y=1(当生产第种容器，即x>0时)或0（当不生产第 种容器即x=0时)。 引入约束x≤My,i=1,2,3,M充分大，以保证当乃=0时，x =0。 建立如下的数学模型： Maxz=4x1+5x2+6x3-100y1-150y2-200y3 s.t. 2X1+4x2+8x3≤500 2x1+32+43≤300 为1+22+3x3≤100 x≤My,i=1,2,3,M充分大 x≥0为0-1变量，i=1,2,3 理运筹学 10

管 理 运 筹 学 10 §3 整数线性规划的应用 解：这是一个整数规划的问题。 设x1，x2， x3 分别为小号容器、中号容器和大号容器的生产数量。 各种容器的固定费用只有在生产该种容器时才投入，为了说明固定费用 的这种性质，设yi = 1(当生产第 i种容器, 即 xi ＞ 0 时) 或0（当不生产第 i种容器即 xi = 0 时）。 引入约束 xi ≤ M yi ，i =1，2，3，M充分大，以保证当yi = 0 时，xi = 0 。 建立如下的数学模型： Max z = 4x1 + 5x2 + 6x3 - 100y1 - 150y2 - 200y3 s.t. 2x1 + 4x2 + 8x3 ≤ 500 2x1 + 3x2 + 4x3 ≤ 300 x1 + 2x2 + 3x3 ≤ 100 xi ≤ M yi ，i =1，2，3，M充分大 xj ≥ 0 yj 为0-1变量，i = 1,2,3