《管理运筹学》课程教学课件（PPT讲稿）第5章 图与网络模型

第五章 图与网络模型 §1图与网络的基本概念 §2最短路问题 §3最小生成树问题 §4最大流问题 §5最小费用最大流问题

管 理 运 筹 学 1 第五章 图与网络模型 §1 图与网络的基本概念 §2 最短路问题 §3 最小生成树问题 §4 最大流问题 §5 最小费用最大流问题

§1 图与网络的基本概念 图论中图是由点和边构成，可以反映一些对象之间的关系。 例如：在一个人群中，对相互认识这个关系我们可以用图 来表示，下图就是一个表示这种关系的图。 赵 e2 (V3)孙 e3 (v4) (W2)钱 李 ·(V)陈 es s)· 周 (v)吴

管 理 运 筹 学 2 §1 图与网络的基本概念 图论中图是由点和边构成，可以反映一些对象之间的关系。 例如：在一个人群中，对相互认识这个关系我们可以用图 来表示，下图就是一个表示这种关系的图。 (v1 ) 赵 (v2 )钱 (v3 )孙 (v4 ) 李 (v5 ) 周 (v6 )吴 (v7 )陈 e2 e1 e3 e4 e5

§11 图与网络的基本概念 当然图论不仅仅是要描述对象之间关系，还要研究特定关 系之间的内在规律，一般情况下图中点的相对位置如何、点与 点之间联线的长短曲直，对于反映对象之间的关系并不是重要 的，如对赵等七人的相互认识关系我们也可以用下图来表示， 可见图论中的图与几何图、工程图是不一样的。 e es 赵 (2)钱孙(w3) 李v) 周(Ws) 吴(v6) 陈(v)

管 理 运 筹 学 3 §1 图与网络的基本概念 当然图论不仅仅是要描述对象之间关系，还要研究特定关 系之间的内在规律，一般情况下图中点的相对位置如何、点与 点之间联线的长短曲直，对于反映对象之间的关系并不是重要 的，如对赵等七人的相互认识关系我们也可以用下图来表示， 可见图论中的图与几何图、工程图是不一样的。 (v1 ) 赵 (v2 )钱 孙(v3 ) 李(v4 ) 周(v5 ) 吴(v6 ) 陈(v7 ) e2 e1 e3 e4 e5

§1 图与网络的基本概念 如果我们把上面例子中的“相互认识”关系改为“认识” 的关系，那么只用两点之间的联线就很难刻画他们之间的关 系了，这是我们引入一个带箭头的联线，称为弧。下图就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。 (V2)钱 as 赵 814 a15 a3 李 a4 ag ()孙 as a6 a12 ()陈 a 3) a10 (v6)吴 周 a13 学 4

管 理 运 筹 学 4 §1 图与网络的基本概念 a1 a2 a3 a4 a14 a7 a8 a9 a a6 5 a10 a12 a11 a13 a15 (v1 ) 赵 (v2 )钱 (v3 )孙 (v4 ) 李 (v5 ) 周 (v6 )吴 (v7 )陈 如果我们把上面例子中的“相互认识”关系改为“认识” 的关系，那么只用两点之间的联线就很难刻画他们之间的关 系了，这是我们引入一个带箭头的联线，称为弧。下图就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示

§1 图与网络的基本概念 无向图： 由点和边构成的图，记作G=(V,E)。 有向图： 由点和弧构成的图，记作D=(V,A)。 连通图： 无向图G,若任何两个不同的点之间，至少存在一条链，则G为 连通图 回路： 若路的第一个点和最后一个点相同，则该路为回路。 赋权图： 对一个无向图G的每一条边(y,V),相应地有一个数w’则称图G 为赋权图，w称为边(W,V)上的权。 网络： 在赋权的有向图D中指定一点，称为发点，指定另一点称为收点？ 其它点称为中间点，并把D中的每一条弧的赋权数称为弧的容量，D就 称为网络

管 理 运 筹 学 5 §1 图与网络的基本概念 ▪ 无向图： 由点和边构成的图，记作G=（V，E）。 • 有向图： 由点和弧构成的图，记作D=（V，A）。 • 连通图： 对无向图G，若任何两个不同的点之间，至少存在一条链，则G为 连通图。 • 回路： 若路的第一个点和最后一个点相同，则该路为回路。 • 赋权图： 对一个无向图G的每一条边(vi ,vj )，相应地有一个数wij，则称图G 为赋权图，wij称为边(vi ,vj )上的权。 • 网络： 在赋权的有向图D中指定一点，称为发点，指定另一点称为收点， 其它点称为中间点，并把D中的每一条弧的赋权数称为弧的容量，D就 称为网络

§2 最短路问题 最短路问题：对一个赋权的有向图D中的指定的两个点V,和V找到一条 从V、到V的路，使得这条路上所有弧的权数的总和最小，这条路被称 之为从V,到V的最短路。这条路上所有弧的权数的总和被称为从V,到V 的距离。 一、求解最短路的Dijkstra:算法（双标号法） 步骤： 1.给出点V1以标号(0，s) 2.找出已标号的点的集合I,没标号的点的集合J以及弧的集合 {(y,v,)y,∈I,v,∈J} 3. 如果上述弧的集合是空集，则计算结束。如果v已标号(，k)，则vs 到v的距离为，而从ⅴ，到v的最短路径，则可以从k反向追踪到起点 V、而得到。如果v,未标号，则可以断言不存在从v,到v的有向路。如果 上述的弧的集合不是空集，则转下一步。 4. 对上述弧的集合中的每一条弧，计算s1l+c。在所有的s中，找到其 值为最小的弧。不妨设此弧为(V,V),则给此弧的终点以双标号 (Scd,c),返回步骤2。 6

管 理 运 筹 学 6 §2 最短路问题 • 最短路问题：对一个赋权的有向图D中的指定的两个点Vs和Vt找到一条 从 Vs 到 Vt 的路，使得这条路上所有弧的权数的总和最小，这条路被称 之为从Vs到Vt的最短路。这条路上所有弧的权数的总和被称为从Vs到Vt 的距离。 一、求解最短路的Dijkstra算法(双标号法） 步骤： 1.给出点V1以标号(0,s) 2.找出已标号的点的集合I，没标号的点的集合J以及弧的集合 3. 如果上述弧的集合是空集，则计算结束。如果vt已标号（l t ,kt），则vs 到vt的距离为l t，而从vs到vt的最短路径，则可以从kt 反向追踪到起点 vs 而得到。如果vt未标号，则可以断言不存在从vs到vt的有向路。如果 上述的弧的集合不是空集，则转下一步。 4. 对上述弧的集合中的每一条弧，计算sij=li+cij 。在所有的sij中，找到其 值为最小的弧。不妨设此弧为（Vc ,Vd），则给此弧的终点以双标号 （scd,c）,返回步骤2。 {( , ) | , } i j i j v v v I v J  

§2最短路问题 例1求下图中v到v的最短路 V3 解：采用Dijkstra算法，可解得最短路径为v1V3V4→V6 各点的标号图如下： (3,1) ,4) V2 7 6 3 3,3)5 5 2 (0s 5 (2,1) 3

管 理 运 筹 学 7 §2 最短路问题 例1 求下图中v1到v6的最短路 解：采用Dijkstra算法，可解得最短路径为v1 v3 v4 v6 各点的标号图如下： v2 3 5 2 7 5 3 1 5 2 1 v1 v6 v v5 3 v4 (3,1) v2 3 5 2 7 5 3 1 5 2 1 V1 （0,s) v5 (8,4) v6 (2,1) v3 (3,3) v4

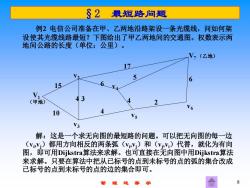
§2 最短路问题 例2电信公司准备在甲、乙两地沿路架设一条光缆线，问如何架 设使其光缆线路最短？下图给出了甲乙两地间的交通图。权数表示两 地间公路的长度（单位：公里）。 V2(乙地) 17 5 6 15 (甲地) 43 2 V6 10 4 V3 解：这是一个求无向图的最短路的问题。可以把无向图的每一边 (VV)都用方向相反的两条弧(VV)和(VY)代替，就化为有向 图，即可用Dijkstra算法来求解。也可直接在无向图中用Dijkstra算法 来求解。只要在算法中把从已标号的点到未标号的点的弧的集合改成 已标号的点到未标号的点的边的集合即可。 曹理运筹学

管 理 运 筹 学 8 §2 最短路问题 例2 电信公司准备在甲、乙两地沿路架设一条光缆线，问如何架 设使其光缆线路最短？下图给出了甲乙两地间的交通图。权数表示两 地间公路的长度（单位：公里）。 解：这是一个求无向图的最短路的问题。可以把无向图的每一边 （vi ,vj）都用方向相反的两条弧（vi ,vj）和（vj ,vi）代替，就化为有向 图，即可用Dijkstra算法来求解。也可直接在无向图中用Dijkstra算法 来求解。只要在算法中把从已标号的点到未标号的点的弧的集合改成 已标号的点到未标号的点的边的集合即可。 V1 （甲地） 15 17 6 2 4 4 4 3 10 6 5 v2 V7 （乙地） v3 v4 v5 v6

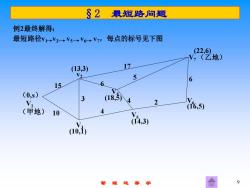
§2 最短路问题 例2最终解得： 最短路径vV3一V一V一V,每点的标号见下图 (22,6 (乙地) (13,3) 17 V2 5 6 15 6 (0,s) 3 (18,5) V 2 16,5) (甲地) 10 4 (T4,3) aod 9

管 理 运 筹 学 9 §2 最短路问题 例2最终解得： 最短路径v1 v3 v5 v6 v7，每点的标号见下图 （0,s） V1 （甲地） 15 17 6 2 4 4 3 10 6 5 (13,3) v2 (22,6) V7 （乙地） V5 (14,3) V6 (16,5) V3 (10,1) V4 (18,5)

§2 最短路问题 例3设备更新问题。某公司使用一台设备，在每年年初，公司就 要决定是购买新的设备还是继续使用旧设备。如果购置新设备，就要 支付一定的购置费，当然新设备的维修费用就低。如果继续使用旧设 备，可以省去购置费，但维修费用就高了。请设计一个五年之内的更 新设备的计划，使得五年内购置费用和维修费用总的支付费用最小。 已知：设备每年年初的价格表 年份 1 2 3 4 5 年初价格 11 11 12 12 13 设备维修费如下表 使用年数 0-1 1-2 2-3 3-4 4-5 每年维修 5 6 8 11 18 费用 10

管 理 运 筹 学 10 §2 最短路问题 例3 设备更新问题。某公司使用一台设备，在每年年初，公司就 要决定是购买新的设备还是继续使用旧设备。如果购置新设备，就要 支付一定的购置费，当然新设备的维修费用就低。如果继续使用旧设 备，可以省去购置费，但维修费用就高了。请设计一个五年之内的更 新设备的计划，使得五年内购置费用和维修费用总的支付费用最小。 已知：设备每年年初的价格表 设备维修费如下表 年份 1 2 3 4 5 年初价格 11 11 12 12 13 使用年数 0-1 1-2 2-3 3-4 4-5 每年维修 费用 5 6 8 11 18