《固体物理学》课程教学课件（PPT讲稿）Chapter 6 Electron motion in the crystal 6.1 The quasi-classical description of Bloch electrons 6.2. Electron quasi-momentum 6.3 The accelerated velocity and effective mass

Chap 6 Electron motion in the crystal Objectives At the end of this Chapter,you should 1.Be able to identify a wave packet in a crystal. 2.Be able to calculate the effective mass at different points in the band. 3.Understand the Electron quasi-momentum hk. 4.Understand the difference of electron motion in k space and real space. 5.Understand the concept of the hole,and understand its motion behavior

Chap 6 Electron motion in the crystal Objectives At the end of this Chapter, you should: 1.Be able to identify a wave packet in a crystal. 2. Be able to calculate the effective mass at different points in the band. 3. Understand the Electron quasi-momentum . 4. Understand the difference of electron motion in k space and real space. 5. Understand the concept of the hole, and understand its motion behavior. k

When I started to think about it,I felt that the main problem was to explain how the electrons could sneak by all the ions in a metal.To my delight,by straight Fourier analysis,I found that the wave differed from the plane wave of free electrons only by a periodic modulation F.BLOCH When an external field (electric and magnetic fields,etc.)is applied to the crystal,the electrons in the crystal does not just feel the role of the external field,but also feel the role of the crystal in a periodic potential.Normally,the external field is much weaker than the crystal periodic potential.Because the periodic field intensity is generally 108 V/cm,very difficult for the external electric field to achieve such magnitude.Therefore,the movement of electrons in the external field in crystal must be discussed based on the eigenstate basis of the periodic field

When I started to think about it, I felt that the main problem was to explain how the electrons could sneak by all the ions in a metal. To my delight，by straight Fourier analysis, I found that the wave differed from the plane wave of free electrons only by a periodic modulation F. BLOCH When an external field (electric and magnetic fields, etc.) is applied to the crystal, the electrons in the crystal does not just feel the role of the external field, but also feel the role of the crystal in a periodic potential. Normally, the external field is much weaker than the crystal periodic potential. Because the periodic field intensity is generally 108 V/cm, very difficult for the external electric field to achieve such magnitude. Therefore, the movement of electrons in the external field in crystal must be discussed based on the eigenstate basis of the periodic field

6.1 The quasi-classical description of Bloch electrons: There are two methods used: Solving the single-electron wave equation in the presence of the external field. Under certain conditions,solving the electronic movement with external field as a quasi-classical particle. Wave equation with external field [+U)-r= Typically,we can only approximately solve the wave equation in the presence of the external field.Very hard. Another method could be considered if:

6.1 The quasi-classical description of Bloch electrons： There are two methods used: Solving the single-electron wave equation in the presence of the external field. Under certain conditions, solving the electronic movement with external field as a quasi-classical particle. Typically, we can only approximately solve the wave equation in the presence of the external field. Very hard. ( ) 2 2 2 U V E m     −  + + =     r Wave equation with external field Another method could be considered if：

The field is weak and constant. Neglect the electronic transitions between different energy bands. Neglect the electron diffraction,interference and collision. This method can be simply used and show a clear physical image. We are willing to adopt it. Classical particle have defined energy and momentum,however,for microscopic particles governed by quantum mechanics,it is valid. Wave packet is often used for the description of quantum state classically,which means that the particles is spatially distributed at ro with uncertainty of Ar.The momentum is hk with uncertainty ofh△k.ro is treated as the centre of the particle,△r△kresults from the uncertainty princible

The field is weak and constant. Neglect the electronic transitions between different energy bands. Neglect the electron diffraction, interference and collision. This method can be simply used and show a clear physical image. We are willing to adopt it. Classical particle have defined energy and momentum, however, for microscopic particles governed by quantum mechanics, it is valid. Wave packet is often used for the description of quantum state classically, which means that the particles is spatially distributed at r0 with uncertainty of △r. The momentum is with uncertainty of . r0 is treated as the centre of the particle, results from the uncertainty princible. k  r k 0 k

Wave packet and electron velocity: In crystal,the quasi-classical movement of e-can be described by wave packet composed of Bloch functions.There are eigenstates with different energy in the wave packet.So,time factor should be considered for the Bloch functions. Firstly,consider the 1D case,assume the wave packet is composed of wave functions in the range of Ak centered at ko Ak is small and we can think that: ,(x)≈，(x)independent ofk. For defined k,the Bloch function with time factor is, y(x,t)=e-a4,(x) @(k)=E(k)/h the neighboring k'states will be mixed with quantum states ko:

Wave packet and electron velocity: In crystal, the quasi-classical movement of e- can be described by wave packet composed of Bloch functions. There are eigenstates with different energy in the wave packet. So, time factor should be considered for the Bloch functions. Firstly, consider the 1D case, assume the wave packet is composed of wave functions in the range of k centered at k0 . k is small and we can think that: ( ) ( ) 0 k k u x u x  independent of k . For defined k , the Bloch function with time factor is, ( ) ( ) , ( ) i kx t k k x t e u x   − =  (k E k ) = ( )/ the neighboring k’ states will be mixed with quantum states k0 :

Wavelet packet 平(x.）-小e4()s⑨-8因 (dk set k=ko+ ())5 x-e4ep〔月d =4,(x)e- 2sim{告[x-(保)1]》 x-(架)1

Wavelet packet ( ) ( ) ( ) 0 2 0 2 , d k k k i kx t k k x t e u x k    + − −  =  ( ) ( ) 0 2 0 0 2 d k k k i kx t k k u x e k    + − −   set 0 k k = + ( ) 0 0 d d k k k        +     ( ) ( ) ( ) 0 0 0 0 2 2 d , exp d d k k i k x t k k x t u x e i x t k       − −          = −                  ( ) ( )  ( )  ( ) 0 0 0 0 0 2 2sin k i k x t k k k d dk d dk x t u x e x t    −    −   =  − ( ) ( ) 0 k k u x u x 

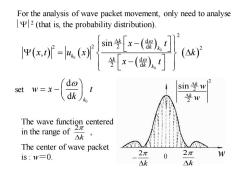
For the analysis of wave packet movement,only need to analyse 2(that is,the probability distribution). e中沿 (ay set w=x- sin学w dk The wave function centered in the range of △k The center of wave packet 2π 0 2π is:w=0. W △k △k

For the analysis of wave packet movement, only need to analyse 2 (that is, the probability distribution). ( ) ( ) ( ) ( ) ( ) 0 0 0 2 2 2 2 d 2 d d 2 d sin , k k k k k k k x t x t u x k x t         −      =        −     set 0 d d k w x t k    = −     2 w k   2 k  −  0 2 2 2 sin k k w w   The wave function centered in the range of , The center of wave packet is : w＝0. 2 k  

do There is x= I=. dk E(k)=ho(k) If the wave packet is a quasi-particle,the particle velocity is The width of Brillouin zone:2/a,assume that Ak is small, generally require Ak>a a △k For 3D case,the velocity of electron is: E

There is 0 0 d 1 d d d k k E x t t k k      = =         If the wave packet is a quasi-particle, the particle velocity is ( ) 0 0 d 1 d d d k x E v k t k   = =     E k k ( ) =  ( ) The width of Brillouin zone: 2/a ，assume that k is small, generally require that is For 3D case, the velocity of electron is: 1 v = k E a k 2   a k   2

For the dispersion of Bloch wave,a stable wave packet requires that the wave vector rangek should be very small. a Considering the uncertainty relation 9,=A≥经Aa suggesting that if the wave packet size is much larger than the cell size,the movement of electrons can be described in terms of wave packet.For transportation,only when the electron mean free path is much larger than the cell size,the electrons in the crystal can be solved as a quasi-classical particle.The motion speed of wave packet (group velocity)is equal to the average velocity of the particles in the center of wave packet

For the dispersion of Bloch wave, a stable wave packet requires that the wave vector range △k should be very small. Considering the uncertainty relation 2 x x    =     p x k x a k 2     x a suggesting that if the wave packet size is much larger than the cell size, the movement of electrons can be described in terms of wave packet. For transportation, only when the electron mean free path is much larger than the cell size, the electrons in the crystal can be solved as a quasi-classical particle. The motion speed of wave packet (group velocity) is equal to the average velocity of the particles in the center of wave packet

important fact 1: The average velocity of electrons are fully determined by energy and wave vector,which is independent of time and space. Therefore,average velocity will keep unchanged without attenuation.This means:the electrons can not be scattered by static atoms.The resistance of a strictly periodic crystal is zero. This point is entirely different from the concept of free electron theory:ion (scattering centers)will affect the average velocity (drift)of the electrons. In other words:If the electron is in a certain state 4k,as long as the lattice periodicity is kept unchanged,the electrons will be in constant motion throughout the crystal with the same velocity. Because the lattice influence on the propagation velocity,have been included in the definition of energy

important fact 1: The average velocity of electrons are fully determined by energy and wave vector, which is independent of time and space. Therefore, average velocity will keep unchanged without attenuation. This means: the electrons can not be scattered by static atoms. The resistance of a strictly periodic crystal is zero. This point is entirely different from the concept of free electron theory: ion (scattering centers) will affect the average velocity (drift) of the electrons. In other words: If the electron is in a certain state , as long as the lattice periodicity is kept unchanged, the electrons will be in constant motion throughout the crystal with the same velocity. Because the lattice influence on the propagation velocity, have been included in the definition of energy.  k