《固体物理学》课程教学课件（PPT讲稿）Chapter 5 band theory 5.6 Density of states（DOS）and Fermi surface 5.7 the electrons in the crystal 5.8 the experimental results for DOS

5.6 Density of states (DOS)and Fermi surface 5.6.1 DOS function AZ:the number of energy states dV-dSdk located in the scope of E~E+AE d △Z DOS function: N(E)=li kx E0△E PBC tell us that N N, All of the k values are uniformly distributed in the k space 01/27

5.6 Density of states (DOS) and Fermi surface 5.6.1 DOS function Z: the number of energy states located in the scope of E~E+E DOS function: 0 ( ) limE Z N E  → E  =  E 3 3 3 2 2 2 1 1 1 b N l b N l b N l k     = + + PBC tell us that All of the k values are uniformly distributed in the k space

The volume occupied by a k spot in the k space 1) (2π) k state density: the state density indexed 2π by the momentum So,the number of wave vectors in (2x)3N2 =N the FBZ is: Ω (2π)月 The surface of E(k)=constant is a surface with the same energy. The volume enclosed by the surface of E and E+AE of is AV

3 (2 ) Vc N N =    3 3 (2 ) (2 )   The volume occupied by a k spot in the k space k state density: So, the number of wave vectors in the FBZ is: the state density indexed by the momentum The surface of E(k)=constant is a surface with the same energy. The volume enclosed by the surface of E and E+ΔE of is V

k So,the number of states is dV=dSdk V ds the perpendicular dissonance between the surface of E and E+AE is dk dkVE=AE (2π) dSdk dkV,E=AB

 = dSdk V Z 3 (2 )  the perpendicular dissonance between the surface of E and E+ΔE is dk So, the number of states is

So,DOS function: Considering the spin of electrons N-2 a)For free electrons 0= h2k2 2m In the k space,the energy of spherical surface with the radius=2mE/ is equivalent

3 ( ) 2 (2 ) k V dS N E  E =     = E V dS N E k 3 (2 ) ( )  Considering the spin of electrons So, DOS function: a) For free electrons In the k space, the energy of spherical surface with the radius is equivalent

On the spherical surface ,小要的 m M两学”E b)The DOS of the NFE The influence of the periodic potential of the crystal on the energy is reflected near the Brilluion zones Take the 2D tetragonal lattice for example,the surface with the same energy is shown as the right image

On the spherical surface 3/ 2 2 2 2 2( ) (2 ) V m E  = b) The DOS of the NFE The influence of the periodic potential of the crystal on the energy is reflected near the Brilluion zones Take the 2D tetragonal lattice for example, the surface with the same energy is shown as the right image

the energy of point A with the wave vector close to the border of the Brilluion zone,is decreased due to the influence of perturbation effect,and the energy surface protrudes toward the border. the energy surface is no longer a whole enclosed surface between the point A and C,but a curved surface disengaged around the apexes

—— the energy of point A with the wave vector close to the border of the Brilluion zone, is decreased due to the influence of perturbation effect, and the energy surface protrudes toward the border. —— the energy surface is no longer a whole enclosed surface between the point A and C， but a curved surface disengaged around the apexes

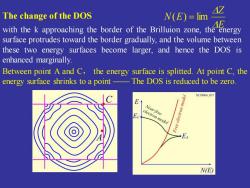
亿 The change of the DOS N(E)=lim E with the k approaching the border of the Brilluion zone,the energy surface protrudes toward the border gradually,and the volume between these two energy surfaces become larger,and hence the DOS is enhanced marginally. Between point A and C,the energy surface is splitted.At point C,the energy surface shrinks to a point -The DOS is reduced to be zero XCH004037 E↑ Near-free electron model EA N(E)

The change of the DOS with the k approaching the border of the Brilluion zone, the energy surface protrudes toward the border gradually, and the volume between these two energy surfaces become larger, and hence the DOS is enhanced marginally. Between point A and C， the energy surface is splitted. At point C, the energy surface shrinks to a point —— The DOS is reduced to be zero. E Z N E   ( ) = lim

The DOS in the second Brilluion zone when E surpasses the pint A in FBZ,the DOS will rapidly increase from zero. E↑ EA EA Band Without overlapping overlappiing Ec>E8 N(E) Ec<EB N(E)

The DOS in the second Brilluion zone —— when E surpasses the pint A in FBZ, the DOS will rapidly increase from zero

c)DOS for the TBA model The s band for scc crystal E*(k)=Eo-2J(cosk,a+cosk a+cosk.a) Near k=0 E6)=Etk+k+） the energy surface is a spherical one with the increase of E,whose energy surface is similar to that of NFE

c) DOS for the TBA model The s band for scc crystal —— the energy surface is a spherical one Near k=0 ( ) 2 (cos cos cos ) E k E0 J1 kx a ky a kz a s = − + + ( ) 2 ( ) 2 2 2 * 2 min x y z k k k m E k = E + + +  ——with the increase of E, whose energy surface is similar to that of NFE

E()=E。-2J(cosk,a+cosk,a+cosk,a） E=2a/）sin2k,a+sin2k,a+sin2k.a） 司 dS N(E)= 、 1 energy sin'ka+sin'k,a+sin2ka) surface =2a )(sin'k,a+sin'k,a+sin'k.a)