《量子力学》课程教学课件（讲稿）Chapter 2 波函数和薛定谔方程 The wave function and Schrödinger Equation

Chapter 2 The waoe junction and Scrodinger Eguation 第二章 波函数与薛定谔方程 The wave function and Schrodinger Equation

1 Chapter 2 The wave function and Schrödinger Equation 第二章 波函数与薛定谔方程 The wave function and Schrödinger Equation

学习内容 Chapter 2 The wave function and Scirdinger Eguation >2.1波函数的统计解释 The Wave function and its statistic explanation >2.2态叠加原理 The principle of superposition > 2.3薛定谔方程 The Schrodinger equation > 2.4粒子流密度和粒子数守恒定律 The current density of particles and conservation laws 2.5定态薛定谔方程 Time independent Schrodinger equation > 2.6一维无限深势阱 The infinite potential well > 2.7线性谐振子 The linear harmonic oscillator > 2.8势垒贯穿 The transmission of potential barrier

2 Chapter 2 The wave function and Schrödinger Equation ¾ 2.1 波函数的统计解释 The Wave function and its statistic explanation ¾ 2.2 态叠加原理 The principle of superposition ¾ 2.3 薛定谔方程 The Schrödinger equation ¾ 2.4 粒子流密度和粒子数守恒定律 The current density of particles and conservation laws ¾ 2.5 定态薛定谔方程 Time independent Schrödinger equation ¾ 2.6 一维无限深势阱 The infinite potential well ¾ 2.7 线性谐振子 The linear harmonic oscillator ¾ 2.8 势垒贯穿 The transmission of potential barrier 学习内容

学习要求 Dhaster 2 The wave function and Scirdinger Eguation 1.理解微观粒子运动状态的描述一 波函数 及其统计解释。 2.通过对实验的分析，理解态叠加原理。 3.掌握微观粒子运动的动力学方程 波函 数随时间演化的规律一 Schrodinger?方程。 4.掌握定态及其性质。 5.通过对三个实例的讨论，掌握定态Schr0 dinger 方程的求解

3 Chapter 2 The wave function and Schrödinger Equation 1.理解微观粒子运动状态的描述 波函数 及其统计解释。 2.通过对实验的分析,理解态叠加原理。 3.掌握微观粒子运动的动力学方程 波函 数随时间演化的规律 SchrÖdinger方程。 4.掌握定态及其性质。 5.通过对三个实例的讨论,掌握定态SchrÖdinger 方程的求解。 学习要求

§2.1波函数的统计解释 Chapter 2 The we junction and Sordinger Eguation 1.微观粒子状态的描述 微观粒子因具有波粒二象性，其运动状态的描 述必有别于经典力学对粒子运动状态的描述，即微 观粒子的运动状态不能用坐标、速度、加速度等物 理量来描述。这就要求在描述微观粒子的运动时， 要有创新的概念和思想来统一波和粒子这样两个在 经典物理中截然不同的物理图像。 德布罗意指出：微观粒子的运动状态可用一个复 函数Ψ（行，）来描述，函数Ψ（行，）一称为波函数。 ★描述自由粒子的波是具有确定能量和动量的平面波

4 Chapter 2 The wave function and Schrödinger Equation 微观粒子因具有波粒二象性，其运动状态的描 述必有别于经典力学对粒子运动状态的描述，即微 观粒子的运动状态不能用坐标、速度、加速度等物 理量来描述。这就要求在描述微观粒子的运动时， 要有创新的概念和思想来统一波和粒子这样两个在 经典物理中截然不同的物理图像。 §2.1 波函数的统计解释 1．微观粒子状态的描述 德布罗意指出：微观粒子的运动状态可用一个复 函数 来描述，函数 — 称为波函数。 Ψ(,) r t G Ψ(,) r t G ★ 描述自由粒子的波是具有确定能量和动量的平面波

§2.1波函数的统计解释（续1） Chapter 2 The waoc junction and Scrodinger Eguation 业p(F,t)=Ae (P.F-Et) de Broglie波 女如果粒子处于随时间和位置变化的力场U(行，)中 运动，他的动量和能量不再是常量（或不同时为常量） 粒子的状态就不能用平面波描写，而必须用较复杂的 波描写，一般记为： Ψ（行，） 三个问题？ 描写粒子状态购 波函数，它通常 是二个复函数。 (1) Ψ是怎样描述粒子的状态呢？ (2)Ψ如何体现波粒二象性的？ (3)Ψ描写的是什么样的波呢？

5 Chapter 2 The wave function and Schrödinger Equation ( ) (,) i P r Et P ψ r t Ae ⋅ − = K K = K K ★如果粒子处于随时间和位置变化的力场 中 运动，他的动量和能量不再是常量（或不同时为常量） 粒子的状态就不能用平面波描写，而必须用较复杂的 波描写，一般记为： Ψ( ,t) rG U , ( ) r t G 描写粒子状态的 波函数，它通常 是一个复函数。 • 三个问题？ (1) ψ 是怎样描述粒子的状态呢？ (2) ψ 如何体现波粒二象性的？ (3) ψ 描写的是什么样的波呢？ de Broglie 波 §2.1 波函数的统计解释（续1）

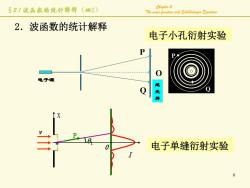
§21霞品煞的镜计解荐（换2） Chapter 2 The waoc junction and Scrodinger Eguation 2.波函数的统计解释 电子小孔衍射实验 D 0 电子源 光屏 电子单缝射实验

6 Chapter 2 The wave function and Schrödinger Equation a v I 0 θ1 X P 电子单缝衍射实验 2．波函数的统计解释 电子源 感 光 屏 P P Q Q O 电子小孔衍射实验 §2.1 波函数的统计解释（续2）

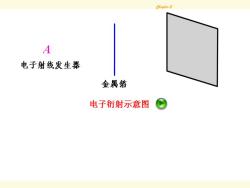
Chaster 2 A 电子射线发生擇 金隅结 电子衍射示意图

7 Chapter 2 The wave function and Schr ödinger Equation

§2.1波函数的统计解释（续3） Chapter 2 The waoc junction and Scrodinger Eguation 两种错误的看法 (1)波由粒子组成 如水波，声波，由物质的分子密度疏密变化而形 成的一种分布。 这种看法是与实验矛盾的，它不能解释长时间单 个电子衍射实验。 电子一个一个地通过小孔，但只要时间足够长， 底片上仍可呈现出衍射花纹。这说明电子的波动性 并不是许多电子在空间聚集在一起时才有的现象， 单个电子就具有波动性。 事实上，正是由于单个电子具有波动性，才能 理解氢原子（只含一个电子！）中电子运动的稳定 性以及能量量子化这样一些量子现象。 8

8 Chapter 2 The wave function and Schrödinger Equation ▲ 两种错误的看法 （1） 波由粒子组成 如水波，声波，由物质的分子密度疏密变化而形 成的一种分布。 这种看法是与实验矛盾的，它不能解释长时间单 个电子衍射实验。 电子一个一个地通过小孔，但只要时间足够长， 底片上仍可呈现出衍射花纹。这说明电子的波动性 并不是许多电子在空间聚集在一起时才有的现象， 单个电子就具有波动性。 事实上，正是由于单个电子具有波动性，才能 理解氢原子（只含一个电子！）中电子运动的稳定 性以及能量量子化这样一些量子现象。 §2.1 波函数的统计解释（续3）

§2.1波函数的统计解释（续4） Chapter 2 The waue junction and ScdingerEgeation 波由粒子组成的看法仅注意到了粒子性的一面，而抹 杀了粒子的波动性的一面，具有片面性。 (2)粒子由波组成 ·电子是波包。把电子波看成是电子的某种实际结构，是 维空间中连续分布的某种物质波包。因此呈现出干涉和 射等波动现象。波包的大小即电子的大小，波包的群速度 即电子的运动速度。 ·什么是波包？波包是各种波数（波长）平面波的迭加。 平面波描写自由粒子，其特点是充满整个空间，这是 因为平面波振幅与位置无关。如果粒子由波组成，那 么自由粒子将充满整个空间，这是没有意义的，与实 验事实相矛盾

9 Chapter 2 The wave function and Schrödinger Equation 波由粒子组成的看法仅注意到了粒子性的一面，而抹 杀了粒子的波动性的一面，具有片面性。 （2） 粒子由波组成 z电子是波包。把电子波看成是电子的某种实际结构,是三 维空间中连续分布的某种物质波包。因此呈现出干涉和衍 射等波动现象。波包的大小即电子的大小,波包的群速度 即电子的运动速度。 §2.1 波函数的统计解释（续4） z什么是波包？波包是各种波数(波长)平面波的迭加。 平面波描写自由粒子,其特点是充满整个空间,这是 因为平面波振幅与位置无关。如果粒子由波组成,那 么自由粒子将充满整个空间,这是没有意义的,与实 验事实相矛盾

§2.1波函数的统计解释（续5） Chapter 2 The wwue junction and Scndinger Eguation ·实验上观测到的电子，总是处于一个小区域内。 例如一个原子内的电子，其广延不会超过原子大小 ≈1A。 ·电子究竟是什么东西呢？是粒子？还是波？ “ 电子既不是粒子也不是波”，既不是经典的粒 子也不是经典的波，但是我们也可以说，“电子既 是粒子也是波，它是粒子和波动二重性矛盾的统一。 这个波不再是经典概念的波，粒子也不是经典概念 中的粒子。 经典概念 1.有一定质量、电荷等“颗粒性”的属性； 中粒子意 2.有确定的运动轨道，每一时刻有一定 味着 位置和速度。 10

10 Chapter 2 The wave function and Schrödinger Equation z 实验上观测到的电子，总是处于一个小区域内。 例如一个原子内的电子，其广延不会超过原子大小 ≈1 。0A z电子究竟是什么东西呢？是粒子？还是波？ “ 电子既不是粒子也不是波 ”，既不是经典的粒 子也不是经典的波，但是我们也可以说，“ 电子既 是粒子也是波，它是粒子和波动二重性矛盾的统一。” 这个波不再是经典概念的波，粒子也不是经典概念 中的粒子。 1.有一定质量、电荷等“颗粒性”的属性; 2．有确定的运动轨道，每一时刻有一定 位置和速度。 经典概念 中粒子意 味着 §2.1 波函数的统计解释（续5）