《量子力学》课程教学资源（习题解答）第三章 量子力学中的力学量

周世勋量子力学教程第三章习题解答 3.1一维谐振子处在基态x)= a V√π (1)势能的平均值可= 222 (2②)动能的平均值T= 4 (3)动量的几率分布函数。 解0=ore@2erh 2a34o2.h o =h@ x2eard在=135.(2n-) 元 4 2a”Va aF-上vaaa V2nEA-aix a方2 ialLods-a[ Vπ2 2a 盟- a2=.o 4u方 =40 (3)c(p)=∫y。(x)w(x)dk

1 周世勋 量子力学教程 第三章习题解答 3.1 一维谐振子处在基态 t x i x e      2 2 2 2 ( ) − − = ，求： (1)势能的平均值 2 2 2 1 U =  x ； (2)动能的平均值 2 2 p T = ； (3)动量的几率分布函数。 解：(1)   − − U = x = x e dx x 2 2 2 2 2 2 2 1 2 1                 =  = =  2 2 2 2 2 2 4 1 2 1 2 1 2 1 2 2 1  4 1 =   + −     − = 0 1 2 2 2 1 3 5 (2 1) a a n x e dx n n n ax   (2)   − = = x p x dx p T ( ) ˆ ( ) 2 1 2 * 2 2       − − − = − e dx dx d e x x 2 2 2 2 2 1 2 2 2 2 1 ( ) 2 1         − − = − x e dx x 2 2 (1 ) 2 2 2 2 2        [ ] 2 2 2 2 2 2 2 2 2    − −  − − = e dx − x e dx  x  x       ] 2 [ 2 3 2 2 2          = −                 = = =  2 2 4 4 2 2 2 2 2  4 1 = 或    4 1 4 1 2 1 T = E −U = − = (3)  c p = x x dx p ( ) ( ) ( ) *  

上层 层产。h a层哈步在 e 2元 点层本 =2 a 动量几率分布函数为 op)-k(p # ah 3.2.氢原子处在基态(，0，p)=- 应 (1)r的平均值： ②势能-上的平均值 (3)最可几半轻. (4)动能的平均值： (5)动量的几率分布函数。 gwr-jrwaofirrern8daoao 汇x"ed= a =433 a 2

2 2 1 2 2 2 1   − − − = e e dx Px i x         − − − = e e dx Px i x   2 2 2 1 2 1       − − + − = e dx ip p x 2 2 2 2 2 2 2 ( ) 2 1 2 1            − − − + = e e dx ip x p 2 2 2 2 2 2 ( ) 2 1 2 2 1                2 2 1 2 2 2 2   p e − = 2 2 2 2 1      p e − = 动量几率分布函数为 2 2 2 1 ( ) ( ) 2       p p c p e − = = # 3.2.氢原子处在基态 0 / 3 0 1 ( , , ) r a e a r − =     ，求： (1)r 的平均值； (2)势能 r e 2 − 的平均值； (3)最可几半径； (4)动能的平均值； (5)动量的几率分布函数。 解：(1)           re r drd d a r r r d r a sin 1 ( , , ) 0 2 2 0 0 2 / 3 0 2 0      − = =   − = 0 3 2 / 3 0 0 4 r a dr a r a   + − = 0 1 ! n n ax a n x e dx 4 0 0 3 0 2 3 2 4 3! a a a =         =

a0-e-云frn0n6o 云em9wo 营d s-4e21 (3)电子出现在r+d球壳内出现的几率为 o(rydr=L(r.0.r'sin 0drd0 do=dr )=4 do(r)=4 (2-2r)re dr ao ao 令do0=0,→5=0,5=0,5=a r 当片=0,5=o时，r)=0为几率最小位置 dio(r)=4 dr2 e0 d'o(r) .r=a。是最可几半径。 1 a T=盆0e gre心pm0a0o e-e灬女 2 do 3

3 0 2 2 0 3 0 2 0 2 / 3 0 2 0 2 0 0 2 / 3 0 2 0 2 0 0 2 / 2 3 0 2 2 2 4 1 4 sin sin 1 (2) ( ) 0 0 0 a e a a e e r dr a e e r drd d a e e r drd d a r e r e U r a r a r a = −         = − = − = − = − = −         −  −  −             (3)电子出现在 r+dr 球壳内出现的几率为   =          0 2 0 2 2 (r)dr [ (r, , )] r sin drd d e r dr a 2r / a 2 3 0 0 4 − = 2 / 2 3 0 0 4 ( ) e r a r − r a  = 0 2 / 0 3 0 ) 2 (2 ( ) 4 r a r re dr a a d r − = −  令 1 2 3 0 0 0, , ( ) r r r a dr d r = ， = =  =  当 r1 = 0, r2 = 时，(r) = 0 为几率最小位置 0 2 2 / 2 0 0 3 0 2 2 ) 8 4 (2 ( ) 4 r a r e a r dr a a d r − = − +  0 ( ) 8 2 3 0 2 2 0 = −  − = e dr a d r r a  ∴ a0 r = 是最可几半径。 (4) 2 2 2 2 ˆ 2 1 ˆ = = −     T p       − −       = − 0 2 0 0 / 2 / 2 3 0 2 [ ( )] sin 1 2 0 0 e e r drd d a T  r a r a     − − = −       0  2 0 0 2 / 2 2 / 3 0 2 [ ( )] sin 1 1 2 0 0 e r drd d dr d r dr d r e a  r a r a   − = − − − 0 / 0 2 0 3 0 2 (2 ) 1 ( 2 4 0 e dr a r r a a r a           +     +      = 2 2 2 2 2 sin 1 (sin ) sin 1 ( ) 1     r   r r r

(⑤)c(p)=「w()w(r,0,p)dr oa动贰成 drdod d-cos 2π 2jharehhel 2π ipr 5owc的h x'e-"dx= a (n为正整数，a心0) 2π 方。1 1 (i( 方p) 1 Aip 2anp元a,i 4 agh √2ah'πa。(a2p2+h2) 、 (2ah)32h z(a2p2+h2)月 动量几率分布函数 8aghs (p)=k(p)=(p 3.3证明氢原子中电子运动所产生的电流密度在球极坐标中的分量是 Jer=Jee=0 Je=chm na加e户 证：电子的电流密度为

4 2 0 2 2 0 2 0 4 0 2 2 ) 4 4 (2 2 4 a a a a    = − = (5) c p  r  r   d p ( ) ( ) ( , , ) *    =     − − =         2 0 0 cos 0 / 2 3 0 3/ 2 sin 1 (2 ) 1 ( ) 0 e r dr e d d a c p pr i r a     = −  − −       0 cos 0 2 / 3 0 3/ 2 ( cos ) (2 ) 2 0 r e dr e d a pr i r a     − − = 0 0 cos 2 / 3 0 3/ 2 0 (2 ) 2      pr i r a e ipr r e dr a      − − = − 0 / 3 0 3/ 2 ( ) (2 ) 2 0 re e e dr a ip pr i pr i r a         + − = 0 1 ! n n ax a n x e dx ( n 为正整数，a>0) ] ) 1 ( 1 ) 1 ( 1 [ (2 ) 2 2 0 2 0 3 0 3/ 2 p i a p i a a ip     + − − =    2 2 2 2 0 0 3 3 0 ) 1 ( 4 2 1    p a a ip a ip + =  2 2 2 2 0 4 4 0 0 3 3 0 2 ( ) 4    + = a p a a  a 2 2 2 2 0 3 / 2 0 ( ) (2 )    + = a p a  动量几率分布函数 2 2 4 0 2 3 5 0 2 ( ) 8 ( ) ( )   + = = a p a p c p   # 3.3 证明氢原子中电子运动所产生的电流密度在球极坐标中的分量是 Jer = Je = 0 2 sin e n m r e m J       = 证：电子的电流密度为

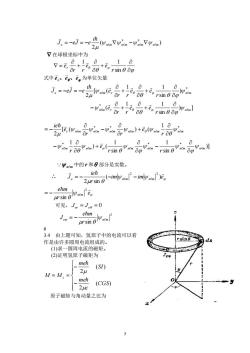
j.=-ej=-eh.@Wz-Yvim-yiwh） 24 又在球极坐标中为 1a rsin 0 do 式中，。，为单位矢量 j。=-ej=-e -Wic(E, -鼎-以景r侧品2 18 vi ro0"a)+,( 品0 Ψm中的r和日部分是实数。 ieh J.=-2ursm0 -imv-imV)e。 ofe 可见，J=J。=0 mgwa 3.4由上题可知，氢原子中的电流可以看 作是由许多圆周电流组成的。 (1)求一圆周电流的磁矩。 (2)证明氢原子磁矩为 meh (S) M=M.= 24 meh 2uc (CGS) 原子磁矩与角动量之比为 5

5 ( ) 2 * * e n m n m n m n m i J eJ e             = − = −  −   在球极坐标中为        +   +    = sin 1 1 r e e r r er    式中   e e e r    、 、 为单位矢量 ) ] sin 1 1 ( ) sin 1 1 [ ( 2 * * n m r n m e n m r n m r e e r r e r e e r r e i J eJ e                               +   +   −   +   +   = − = − )] sin 1 sin 1 ) ( 1 1 [ ( ) ( 2 * * * * * * n m n m n m n m n m n m r n m n m n m n m n m n m r r e r r e r r e ie                                        −   +   −   +   −   = −  nm 中的 r 和  部分是实数。 ∴      im im e r ie Je n m n m      ( ) 2 sin 2 2 = − − −     e r e m n m    2 sin = − 可见， Jer = Je = 0 2 sin e n m r e m J       = − # 3.4 由上题可知，氢原子中的电流可以看 作是由许多圆周电流组成的。 (1)求一圆周电流的磁矩。 (2)证明氢原子磁矩为        − − = = ( ) 2 ( ) 2 CGS c me SI me M M z     原子磁矩与角动量之比为

(e (S M. 24 L. e 2uc (CGS) 这个比值称为回转磁比率。 解：(1)一圆周电流的磁矩为 dM=iA=JndS·A(i为圆周电流，A为圆周所围面积) s、eim -snG加w'ds.(rsin =-ehm πrsin「dS =-ehmsin wdrd0 (ds rdrde) (2)氢原子的磁矩为 M-aM=[-imr产sm8din chm sindndo 24 =-gzwafrsn6dnaio ehm 2 (S0 在CGS单位制中M=-m 2uc 原子磁矩与角动量之比为 M.=M e M. e (S) (CGS)# 35一刚性转子转动惯量为1，它的能量的经典表示式是H=)号，L为 角动量，求与此对应的量子体系在下列情况下的定态能量及波函数： 转子绕一固定轴转动： 转子绕一固定点转动： 解：()设该固定轴沿Z轴方向，则有 2= 6

6        − − = ( ) 2 ( ) 2 CGS c e SI e L M z z   这个比值称为回转磁比率。 解：(1) 一圆周电流的磁矩为 dM = iA = JedS  A （ i 为圆周电流， A 为圆周所围面积） 2 2 ( sin ) sin      dS r r e m n m = −    r dS e m n m 2 sin      = −     r drd e m n m 2 2 sin   = − (dS = rdrd) (2)氢原子的磁矩为     = = −     0 0  2 2 r sin drd e m M dM nm     = −        0 0 2 2 2 sin 2 r drd e m nm         r drd d e m    n m  = − 2 0 0 0 2 2 sin 2   2 em = − (SI) 在 CGS 单位制中 c e m M 2  == − 原子磁矩与角动量之比为 ( ) 2 SI e L M L M z z z  = = − ( ) 2 CGS c e L M z z  = − # 3.5 一刚性转子转动惯量为 I，它的能量的经典表示式是 I L H 2 2 = ，L 为 角动量，求与此对应的量子体系在下列情况下的定态能量及波函数： 转子绕一固定轴转动： 转子绕一固定点转动： 解：(1)设该固定轴沿 Z 轴方向，则有 2 2 L = LZ

哈米顿算符 a-引p 方d2 其本征方程为（户与1无关，属定态问题） 方2d2 21 dp)=Edp) )2IE do p) 令m2=2E ,则 do)+m)=0 do 取其解为(p)=Aemp (m可正可负可为零) 由波函数的单值性，应有 p+2π)=glp)→eme+2w)=eme 即e2m=1 m=0,土1，±2，. 转子的能能量为E,- (m=0,±1，±2，) 可见能量只能取一系列分立值，构成分立谱。 定态波函数为 Bu =Aeime A为归一化常数，由归一化条件 1=p.d0=Ado=2π 1 →A=2 ∴转子的归一化波函数为 中n2r 综上所述，除m=0外，能级是二重简并的 (2)取固定点为坐标原点，则转子的哈米顿算符为 与1无关，属定态问题，其本征方程为 7

7 哈米顿算符 2 2 2 2 2 ˆ 2 1 ˆ d d I L I H Z  = = − 其本征方程为 ( H与t ˆ 无关，属定态问题) ( ) ( ) 2 ( ) ( ) 2 2 2 2 2 2 2             IE d d E d d I = − − = 令 2 2 2  IE m = ，则 ( ) 0 ( ) 2 2 2 +   =    m d d 取其解为    im ( ) = Ae ( m 可正可负可为零) 由波函数的单值性，应有         im im + =  e = e ( +2 ) ( 2 ) ( ) 即 1 2 = i m e ∴m= 0，±1，±2，. 转子的定态能量为 I m Em 2 2 2  = (m= 0，±1，±2，.) 可见能量只能取一系列分立值，构成分立谱。 定态波函数为   im m = Ae A 为归一化常数，由归一化条件         2 1 1 2 2 2 0 2 2 0 *  = = = =   A m md A d A ∴ 转子的归一化波函数为    im m e 2 1 = 综上所述，除 m=0 外，能级是二重简并的。 (2)取固定点为坐标原点，则转子的哈米顿算符为 ˆ 2 2 1 ˆ L I H = H与t ˆ 无关，属定态问题，其本征方程为

(.p)-EY(0.p) (式中Y(0,p)设为户的本征函数，E为其本征值) 2Y(8,p)=2IEr(8,p) 令2E=2,则有 2Y(0,p)=h2Y(0,p) 此即为角动量？的本征方程，其本征值为 2=22=(+10h2 (0=0,1,2,) 其波函数为球谐函数Yn(O,p)=NnP州(cosO)emp ∴转子的定态能量为 E=(c+h 2 可见，能量是分立的，且是(2(+1)重简并的。 3.6设=0时，粒子的状态为 (x)=Alsinkx+cos kx] 求此时粒子的平均动量和平均动能。 w(x)=Alsin2kx+coskx]=l(1-cos2kx)+coskx] =1-cos2kx +coskoxl =2l-e-ea)+5e+e】 _42通1e-c业-e+e+e小2 2 (已经展开为动量本征函数的形式了) 可见，动量P,的可能值为 02防 -2 动能广的可能值为0 2k2h22k2h2 k2h2 k2h2 24 24 24 对应的几率0n应为p.84(4)】 A2 A A A A 16 6 6 62城 (5 8 8 令4办

8 ( , ) ( , ) ˆ 2 1 2 L Y   EY   I = (式中 Y( ,) 设为 H ˆ 的本征函数， E 为其本征值) ( , ) 2 ( , ) ˆ 2 L Y   = IEY   令 2 2IE =  ，则有 ( , ) ( , ) ˆ 2 2 L Y   =  Y   此即为角动量 2 L ˆ 的本征方程，其本征值为 ( 1) ( 0, 1, 2, ) L 2 =  2 =   +  2  =  其波函数为球谐函数     m im m m Y ( , ) N P (cos )e  =   ∴ 转子的定态能量为 2 ( 1) 2 I E     + = 可见，能量是分立的，且是 (2 + 1) 重简并的。 # 3.6 设 t=0 时，粒子的状态为 ( ) [sin cos ] 2 2 1  x = A kx + kx 求此时粒子的平均动量和平均动能。 解： ( ) [sin cos ] [ (1 cos 2 ) cos ] 2 1 2 1 2 2 1  x = A k x + k x = A − k x + k x [1 cos2 cos ] 2 kx kx A = − + [1 ( ) ( )] 2 2 2 2 1 2 1 i kx i kx ikx ikx e e e e A − − = − − + +     2 1 [ ] 2 2 2 1 2 2 1 2 2 1 2 0 1 = − − + +  i x i kx −i kx ikx −ikx e e e e e A （已经展开为动量本征函数的形式了） 可见，动量 n p 的可能值为 0 2k − 2k k − k 动能 2 2 n p 的可能值为    2 2 2 2 0 2 2 2 2 2 2 2 2 k  k  k  k  对应的几率 n 应为[ p.84(4) ] ) 2 16 16 16 16 4 ( 2 2 2 2 2  A A A A A  2 ) 8 1 8 1 8 1 8 1 2 1 (  A

上述的A为归一化常数，可由归一化条件，得 1-2@,=f+4 62城= 2.2 A=1/√ ∴动量p的平均值为 p=p.0 =0+2hx 16 2h-2h×4 16 2+hx .2劢=0 16 2-hx4 16 -0+24n×2+× 81 2h8*2 -5k2h2 3.7一维运动粒子的状态是 w(x)= [Arex,当r20 0, 当r0，求 ()粒子动量的几率分布函数： (2)粒子的平均动量。 解：（①先求归一化常数，由 1=vxd=fxed 2分4？ 1 ∴.A=22/2 x)=222xe(x≥0 Ψ(x)=0 (x<0) 动量为自变量的本征函数为： 4p- =ey(x)dx=( a2ea 9

9 上述的 A 为归一化常数，可由归一化条件，得   2 2 ) 2 16 4 4 1 ( 2 2 2 =  = +   =  A A A n n ∴ A = 1/  ∴ 动量 p 的平均值为 2 0 16 2 16 2 16 2 2 16 0 2 2 2 2 2 = +   −   +   −   = =           A k A k A k A k p p n n n = =  n n p pn T  2 2 2 2 2 8 1 2 2 8 2 1 0 2 2 2 2 = +   +     k  k  8 5 2 2 k  = # 3.7 一维运动粒子的状态是      = − 0, 0 , 0 ( ) x Axe x x x 当  当  其中   0 ，求： (1)粒子动量的几率分布函数； (2)粒子的平均动量。 解：(1)先求归一化常数，由    −  − = = 0 2 2 2 2 1 (x) dx A x e dx x  2 3 4 1 A  = ∴ 3 / 2 A = 2 x x xe    − = 3/ 2 ( ) 2 ( x  0)  ( x) = 0 ( x  0) 动量为自变量的本征函数为： 1 1 1/ 2 3/ 2 ( ) ( ) ( ) ( ) 2 2 2 ikx ik x c p e x dx xe dx        − − + − − = =   

x 1 2劢 元+k e+云+庆e肉 2 x 221 =(2a+i=(2 (+i 动量几率分布为 a(p)=c(p)= 2212231 而伏+T+网 an=上yir恤=-4e太e达 =-ih422x1-x)e2 =-ih4（x-x2)e2d 1 =4玩绿 =0 或者，p=∫c*pcdp=.=0 3.8.在一维无限深势阱中运动的粒子，势阱的宽度为a,如果粒子的状态 由波函数 V(x)=Ax(a-x) 描写，A为归一化常数，求粒子的几率分布和能量的平均值。 解：由波函数(x)的形式可知一维无限深势阱的分布如图示。粒子 能量的本征函数和本征值为 ,巨sim5x,0sxsa V a (x) (0 x≤0，x2a (n=1,2,3, 能量的几率分布函数为o(E)=C广.p.832)

10 ] 1 ) [ 2 2 ( ( ) 0 1/ 2 ( ) 3   − − +  − + + + + = − e dx ik e ik x  ik x  ik x      2 1 / 2 3 2 1 / 2 3 ( ) 1 ) 2 2 ( ( ) ) 2 2 (    p i ik x + = = + =       动量几率分布为 2 2 2 2 3 3 2 2 2 2 3 2 ( ) 2 1 ( ) 2 1 ( ) ( ) p p p c p + = + = =            (2)    − − −  − = = − e dx dx d p x p x dx i xe x x ( ) ˆ ( ) 4 ( ) * 3       3 2 4 (1 ) x i x x e dx     − − = − −  3 2 2 4 ( ) x i x x e dx     − − = − −  3 2 2 1 1 4 ( ) 4 4 i    = − − = 0 或者， = * = = 0   − p c pcdp  # 3.8.在一维无限深势阱中运动的粒子，势阱的宽度为 a ，如果粒子的状态 由波函数 (x) = Ax(a − x) 描写，A 为归一化常数，求粒子的几率分布和能量的平均值。 解：由波函数 (x) 的形式可知一维无限深势阱的分布如图示。粒子 能量的本征函数和本征值为          x x a x x a a n x a 0, 0, sin , 0 2 ( )   ＝          x x a x x a a n x a 0, 0, sin , 0 2 ( )   2 2 2 2 2 a n En    = (n = 1，2，3， ) 能量的几率分布函数为 2 ( )  E = Cn . [p.83(2)]