《量子力学》课程教学资源（习题解答）第七章 自旋与角动量、全同粒子体系

第七章自旋与全同粒子 7.1证明：666：=i 证：由对易关系66，-6,6.=2i6: 及 反对易关系G6,+6,6=0， 得 6.6,=i6 上式两边乘6，得 66,6=i6 62=1 ∴66,6=i 7.2求在自旋态(S)中，5和5，的测不准关系： (4S)2(4S,)2=? 解：在5，表象中x(S)、S、S,的矩阵表示分别为 48)-0-北周80。 在x8)态中可-x对9,4-00000-0 及-=0008调-号 -8-5-4 1

1 7.2 求在自旋态 ( ) 2 1  Sz 中， Sx ˆ 和 Sy ˆ 的测不准关系： ( ) ( ) ? 2 2 Sx Sy = 解：在 Sz ˆ 表象中 ( ) 2 1  Sz 、 Sx ˆ 、 Sy ˆ 的矩阵表示分别为         = 0 1 ( ) 2 1  Sz         = 1 0 0 1 2 ˆ  Sx         − = 0 0 2 ˆ i i S y  0 4 1 1 0 0 1 1 0 2 0 1 2 (1 0) ˆ 2 2 2 2 1 2 1    =                        = = + Sx  Sx  4 ( ) 2 2 2 2  Sx = Sx − Sx = ∴ 在 ( ) 2 1  Sz 态中 0 0 1 1 0 0 1 2 (1 0) 2 1 2 1 =                = = +  Sx  Sx 7.1.证明： i x y z  ˆ  ˆ  ˆ = 证：由对易关系 x y y x z  ˆ  ˆ − ˆ  ˆ = 2i ˆ 及 反对易关系 ˆ x ˆ y +  ˆ y ˆ x = 0 ， 得 x y z  ˆ  ˆ = i ˆ 上式两边乘  z ˆ ，得 2 ˆ ˆ ˆ ˆ x y z z    = i ∵ ˆ 1 2  z = ∴ i  ˆ x ˆ y ˆ z = 第七章 自旋与全同粒子

=x84=100=0 =对x4=0o0）00-号 四-可 ssF-名 讨论：由5、5，的对易关系 [心，S1=8 器 要求a,产a,之 4 在x心)态中，耳=号 :西四落 可见①式符合上式的要求。 73求-60，-的本征值和 所属的本征函数。 解：S的久期方程为 2=0 -身=0→及=号 2 :及的本征值为±号

2 0 0 1 0 0 2 (1 0) ˆ 2 1 2 1 =                − = = + i i Sy Sy    0 4 1 0 0 0 2 0 2 (1 0) ˆ 2 2 2 2 1 2 1    =                −         − = = + i i i i Sy  Sy 4 ( ) 2 2 2 2  Sy = Sy − Sy = 16 ( ) ( ) 4 2 2  Sx Sy = 16 ( ) ( ) 4 2 2  Sx Sy = 讨论：由 Sx ˆ 、 Sy ˆ 的对易关系 [ Sx ˆ ， Sy ˆ ] Sz i ˆ =  要求 4 ( ) ( ) 2 2 2 2 z x y S S S     在 ( ) 2 1  Sz 态中， 2  Sz = ∴ 16 ( ) ( ) 4 2 2  Sx Sy  可见①式符合上式的要求。 7.3.求         − − =         = 0 0 2 ˆ 1 0 0 1 2 ˆ i i Sx S y   及 的本征值和 所属的本征函数。 解： Sx ˆ 的久期方程为 0 2 2 = − −     2 ) 0 2 ( 2  2   − =   =  ∴ Sx ˆ 的本征值为 2  

7.4求自旋角动量(cosa,cosB,cos）方向的投影 即 =成o+5c0+项cogA方 2a,=1 a1= 寿惩绰梨鞭履的笨酱数为、2= 11 在这些本猛态中，测量5，有哪些可能值？以丛可 能值各以多大的几率出现？S,的平均值是多少？ →（份）（公）6=4 即2a2=1∴. :。方 对应于本征值-的本征函数为：= 11 同理可求得5，的本征值为土号。其相应的本征西数分别为 4周

3 即 2 1 2 a1 = ∴ 2 1 2 1 a1 = b1 = 对应于本征值 2  的本征函数为         = 1 1 2 1 1/ 2 2 2 2 2 2 2 b a b a a b  = −         − − =         同理可求得 Sy ˆ 的本征值为 2   。其相应的本征函数分别为         = i 1 2 1 2  1         − = − i 1 2 1 2  1 即 2 1 2 a2 = ∴ 2 1 2 1 a2 = b2 = − 对应于本征值 2  − 的本征函数为         − − = 1 1 2 1  1/ 2 7.4 求自旋角动量 (cos,cos ,cos ) 方向的投影   cos ˆ cos ˆ cos ˆ ˆ n x y z S = S + S + S 本征值和所属的本征函数。 在这些本征态中，测量 Sz ˆ 有哪些可能值？这些可 能值各以多大的几率出现？ Sz ˆ 的平均值是多少？

7.4求自旋角动量(cosa,cosB,cos)方向的投影 S.=S.coa+S,co8+S.cox 本征值和所属的本征函数。 在这些本征态中，测量有哪些可能值？这些可 能值各以多大的几率出现？S,的平均值是多少？ 解：在3。表象，3m的矩阵元为 -0a+Cm+0s .gs -cosy 其相应的久期方程为 2os7-2osa-ios =0 3(eosa+icos月）-cos7-2 22、h2 cos2yh (cos2 a+cos0 即 R-F-0(利用c0s2a+cos2B+cos27=) 4

4 解：在 Sz ˆ 表象， Sn ˆ 的矩阵元为   cos 0 1 1 0 2 cos 0 0 2 cos 1 0 0 1 2 ˆ         − +         − +         =    i i Sn 7.4 求自旋角动量 (cos,cos ,cos ) 方向的投影   cos ˆ cos ˆ cos ˆ ˆ Sn = Sx + Sy + Sz 本征值和所属的本征函数。 在这些本征态中，测量 Sz ˆ 有哪些可能值？这些可 能值各以多大的几率出现？ Sz ˆ 的平均值是多少？         + − − =       cos cos cos cos cos cos 2 i i Sn  其相应的久期方程为 0 cos 2 (cos cos ) 2 (cos cos ) 2 cos 2 = + − − − −             i i 即 (cos cos ) 0 4 cos 4 2 2 2 2 2 2  −  −  +  =   0 4 2 2 − =   ( cos cos cos 1) 2 2 2 利用  +  +  =

。=号 所拟或的本证值为±号 设对应于8.一受的本证函数的矩库表示为x46,)-日】 则 h cosy 2 cosa+icos B r8-8 -cosy a(cosa+icos B)-bcosy=b b=cosa+icosB 1+cos7 由归一化条件，得 1=x4-a68=+f ldcosatreosa1 1+cosy 取a=2 +c0里，得b=0+ic0 √2(1+c0) 1+cosy 名S)= cosa+icosB 2(1+cosy)

5  2   =  所以 Sn ˆ 的本征值为 2   。 设对应于 2  Sn = 的本征函数的矩阵表示为         = b a Sn ( ) 2  1 ， 则         =                + − − b a b a i i cos cos cos 2 cos cos cos 2          a(cos + i cos ) −bcos = b    1 cos cos cos + + = i b 由归一化条件，得 2 2 * * 1 ( , ) 2 1 2 1 a b b a a b = +         = = +   1 1 cos cos cos 2 2 2 = + + + a i a    1 1 cos 2 2 = + a  取 2 1+ cos a = ，得 2(1 cos ) cos cos    + + = i b             + + + = 2(1 cos ) cos cos 1 1 cos ( ) 2 1      i Sn

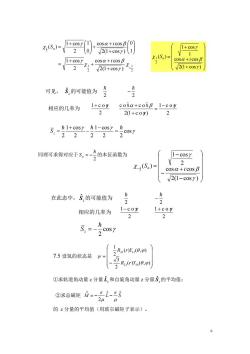
2(0V21+cosy)1 1+cos 1+cosy cosa+icosB (S)= cosa+icos B F2+V20+c0s7 V2(1+cos7) 可见，令的可能值为身 相应的几率为 1+c0y cosa+co3β_1-coy 2 21+co) -+2-oy 2222 同理可求得对应于5，=一号的本征函数为 1-cosy 2 Z(S,)= cosa+icos B 2(1-cosy) 在此态中，S,的可能值为 h 相应的几率为 1-cos 1+cox 2 2 7.5设氢的状态是Ψ= ①求轨道角动量z分量L,和自旋角动量z分量3的平均值： ②求总磁能成：一 的z分量的平均值（用玻尔磁矩子表示）。 6

6             + + + = 2(1 cos ) cos cos 1 1 cos ( ) 2 1      i Sn 2 1 2 1 2(1 cos ) cos cos 2 1 cos 1 0 2(1 cos ) cos cos 0 1 2 1 cos ( ) 2 1 + − + + + =         + + +       +  =            i i Sn 可见， Sz ˆ 的可能值为 2 2   − 相应的几率为 2 1+ cos 2 1 cos 2(1 cos) cos cos 2 2     − = + +    cos 2 2 1 cos 2 2 1 cos 2    = − − + Sz = 同理可求得对应于 2  Sn = − 的本征函数为 在此态中， Sz ˆ 的可能值为 2 2   − 相应的几率为 2 1− cos 2 1+ cos             − + − − = − 2(1 cos ) cos cos 2 1 cos ( ) 2 1      i Sn cos 2  Sz = − 7.5 设氢的状态是             − = ( ) ( , ) 2 3 ( ) ( , ) 2 1 21 10 21 11      R r Y R r Y ①求轨道角动量 z 分量 Lz ˆ 和自旋角动量 z 分量 Sz ˆ 的平均值； ②求总磁矩 S e L e M ˆ ˆ 2 ˆ      = − − 的 z 分量的平均值（用玻尔磁矩子表示）

t可成v-ao9oa.o周 -s.(l0.wz(5)-5k.(Y.0.z.5) 从中的表达式中可看出，的可能值为方0 相应的几率为 曰元-4 5,的可能值为登一分相应的几率C s-8s好身 品8=品骨骨0学 7.6一体系由三个全同的玻色子组成，玻色子之间无相互作用。玻色子只 有两个可能的单粒子态。问体系可能的状态有几个？它们的波函数怎样用 单粒子波函数构成？ 解：体系可能的状态有4个。设两个单粒子态为4， 中，则体系可能的状态为 Φ，=4(q1)4(q2)4(q3)Φ2=中，(91)中，(q2)p,(93) D=54(9g:,g)+4,(g） +4,(q2)-,(q3)p,(41】 。=5[,(q)中，(，(g)+,(4中，(q0(q2） +中，(q2)p(q3)中(q】

7 解：ψ可改写成         −        = 1 0 ( ) ( , ) 2 3 0 1 ( ) ( , ) 2 1  R21 r Y11   R21 r Y10   ( ) ( , ) ( ) 2 3 ( ) ( , ) ( ) 2 1 2 2 1 1 0 1 2 2 1 1 1 1 z Y Sz R r Y S R r − =    −    从ψ的表达式中可看出 Lz ˆ 的可能值为  0 相应的几率为 4 1 4 3 4   Lz = Sz ˆ 的可能值为 2  ， 2  − 。相应的几率 2 Ci 为 4 1 ， 4 3 。 4 4 3 4 2 1 2 2    Sz =  Ci Szi =  −  = − ) 4 ( 2 2 4   = − − = −  −  −     e e S e L e Mz z z MB e 4 1 2 4 =  =   7.6 一体系由三个全同的玻色子组成，玻色子之间无相互作用。玻色子只 有两个可能的单粒子态。问体系可能的状态有几个？它们的波函数怎样用 单粒子波函数构成？ 解：体系可能的状态有 4 个。设两个单粒子态为 i ，  j ，则体系可能的状态为 ( ) ( ) ( ) 1 =i q1 i q2 i q3 ( ) ( ) ( ) 2 =  j q1  j q2  j q3 ( ) ( ) ( )] [ ( ) ( ) ( ) ( ) ( ) ( ) 3 1 2 3 1 3 1 2 3 1 3 2 q q q q q q q q q i i j i i j i i j           + = + ( ) ( ) ( )] [ ( ) ( ) ( ) ( ) ( ) ( ) 3 1 2 3 1 4 1 2 3 1 3 2 q q q q q q q q q j j i j j i j j i           + = +

7.7证明x”,x,xX和x,组成的正交归一系。 解xS”x=[%2(S-)X2(S2.[12(S-)x2(S2.】 =X2(S2.)X2(S1-)X2(Se)12(S2:) =X2(S2-)X2(S2=)=1 x0x2=[x2(S)x12(S2.J[z-2(S.)x-2(S2.】 =Xt2(S2:)xt2(S1-)X12(S:)X12(S2.)=0 增发-方a.a低川. ·[x1w2(S1:)X-/2(S2=)+X-12(S:)X1/2(S2:] -xi(S.)zi(.)zu:(S.)z-(S.)+ +2(S2:)X2(S1:)x2(S:)%12(S2.J =方i,z8,0=0 同理可证其它的正交归一关系。 zv(5).)+(). [X2(S1-)X-2(S2.)+X-2(S1-)X2(S2.】 8

8 [ ( ) ( ) ( ) ( )] [ ( ) ( )] 2 1 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 (1) (3) z z z z S S z z S S S S S S         − − + +  + =  ( ) ( ) ( ) ( )] [ ( ) ( ) ( ) ( ) 2 1 1/ 2 2 1/ 2 1 1/ 2 1 1/ 2 2 1/ 2 2 1/ 2 1 1/ 2 1 1/ 2 2 z z z z z z z z S S S S S S S S         − + + − + + + = + [ ( ) ( ) 0] 2 1 = 1 / 2 2 − 1 / 2 2 + +  S z  S z = 0 同理可证其它的正交归一关系。 [ ( ) ( ) ( ) ( )] [ ( ) ( ) ( ) ( )] 2 1 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 (3) (3) z z z z S S z z z z S S S S S S S S           − − + − − +  + = +  7.7 证明 (1) (2) (3) , ,  S  S  S 和  A组成的正交归一系。 解 [ ( ) ( )] [ ( ) ( )] 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 (1) (1) S S z z z z    S  S  S  S + + = ( ) ( ) ( ) ( ) 1/ 2 S2z 1/ 2 S1z 1/ 2 S1z 1/ 2 S2z + + = ( ) ( )  1 / 2 S2z  1 / 2 S2z + = = 1 [ ( ) ( )] [ ( ) ( )] 1/ 2 1 1/ 2 2 1/ 2 1 1/ 2 2 (1) (2) S S S z S z − S z − S z + +   =     ( ) ( ) ( ) ( ) 1/ 2 S2z 1/ 2 S1z −1/ 2 S1z −1/ 2 S2z + + =     = 0

=xa&.x-(5.FIzr(S.zs.】 +zv(S)z-v(S:.T[zv:(S.)z-v2(S +aSzn6.rz6.zn】 +[名(S.)x2(Sr[x2(S.)z2(S〗 =0+0+1 7.8设两电子在弹性辏力场中运动，每个电子的势能是 U)=)4o。如果电子之间的库仑能和U)相比可以忽略， 求当一个电子处在基态，另一电子处于沿x方向运动的第一激发 态时，两电子组成体系的波函数。 解：电子波函数的空间部分满足定态S-方程 ()(()EMK) 方2 )Evr) h2,82.a2.a2 2,0282.2、 2u(r)+Hrv(r)=Ev(r) 考虑到r2=x2+y2+2,令(r)=X(x)Y(y)Z()

9 [ ( ) ( )] [ ( ) ( )] 2 1 1/ 2 S1z 1/ 2 S2z 1/ 2 S2z −1/ 2 S1z + +   −   [ ( ) ( )] [ ( ) ( )] 2 1 1/ 2 S2z 1/ 2 S1z 1/ 2 S1z −1/ 2 S1z + +   −   [ ( ) ( )] [ ( ) ( )] 2 1 1/ 2 S2z 1/ 2 S1z 1/ 2 S2z −1/ 2 S1z + +   −   1 2 1 0 0 2 1 = + + + = [ ( ) ( )] [ ( ) ( )] 2 1 1/ 2 S1z 1/ 2 S2z 1/ 2 S1z −1/ 2 S2z + =   −   7.8 设两电子在弹性辏力场中运动，每个电子的势能是 2 2 2 1 U(r) =  r 。如果电子之间的库仑能和U (r) 相比可以忽略， 求当一个电子处在基态，另一电子处于沿 x 方向运动的第一激发 态时，两电子组成体系的波函数。 解：电子波函数的空间部分满足定态S-方程 ( ) ( ) ( ) ( ) 2 2  r U r  r E r  −  + =  ( ) ( ) 2 1 ( ) ( ) 2 2 2 2 2 2 2 2 2 2 r r r E r x y z      + =   +   +   −  ( ) ( ) 2 1 ( ) ( ) 2 2 2 2 2 2 2 2 2 2 r r r E r x y z      + =   +   +   −  考虑到 2 2 2 2 r = x + y + z ，令  (r) = X (x)Y( y)Z(z)

2na+0+z+2o'(x2+y2+:3z=Ez （w-(}w 21a2y+1 +(1az,1 2uZa2+24w2:3)=E →器=6 票+m-民5=+8 2器· 其中水=20a=贸 三X,的=N.e产H(a)y.0=NeH.a) Z,e=N,eH,a） w.(r)-N.N-NeH.(ax)H1(@y)H(a=) v-(r)-N.N.N.eH.(co)(@/)H.c) Emc =(n+m++)h@ 对于基态n=m=(=0,H。=1 Pw。=wmo=（。中】 对于沿x方向的第一激发态n=1,m=(=0, H(x)=2ax

10 XYZ x y z XYZ EXYZ x y z + + + =   +   +   − ( ) 2 1 ( ) 2 2 2 2 2 2 2 2 2 2 2 2    z E x Z Z y x Y Y x x X X + =   + − +   + + −   − ) 2 1 1 2 ( ) 2 1 1 2 ) ( 2 1 1 2 ( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2          Ex x x X X + =    − ) 2 1 1 2 ( 2 2 2 2 2    Ey y x Y Y + =   − ) 2 1 1 2 ( 2 2 2 2 2    E Ex Ey Ez = + + Ez z x Z Z + =   − ) 2 1 1 2 ( 2 2 2 2 2    其中 2 ! 1/ 2 n Nn n   = ，    = ( ) ( ) 2 2 2 1 X x N e H x n x n n  −   = ( ) ( ) 2 2 2 1 Y y N e H y m y m m  −  = ( ) ( ) 2 2 2 1 Z z N e H z z      − = ( ) ( ) ( ) ( ) 2 2 2 1 r N N N e H x H y H z n m r  n m n m        − = ( ) ( ) ( ) ( ) 2 2 2 1 r N N N e H x H y H z n m r  nm n m        − = Enm = (n + m +  + 2 3 ) 对于基态n = m =  = 0， 1 0 H = 2 2 r 2 1 3/ 2 0 000 (r) ( ) e      −  = = 对 于 沿 χ 方 向 的 第 一 激 发 态 n =1，m =  = 0 ， H x) 2 x （1 = 