《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.3 Nearly Free Electron 5.4 BZ and energy bands

5.3 Nearly Free Electron The potential of electron is weaker than the kinetics of electron, and the motion could be seen as almost free.So,free electron motion is supposed to be the zeroth order approximation and the influence of periodical potential is regarded as the perturbation.at the same time,the motion must also obeys the symmetry condition This model is called empty lattice model. potential U ion core 1D periodical potential field for the electrons in the crystal
5.3 Nearly Free Electron The potential of electron is weaker than the kinetics of electron, and the motion could be seen as almost free. So, free electron motion is supposed to be the zeroth order approximation and the influence of periodical potential is regarded as the perturbation. at the same time, the motion must also obeys the symmetry condition. This model is called empty lattice model. 1D periodical potential field for the electrons in the crystal

for the case of 1D,the state function and energy for the empty lattice model should be: 1 2m where 0 indicates the solution with no perturbation.The relation between energy and wave vector is parabolic.Considering the requirement of symmetry,it is splitted into many parts.The energy of any two equivalent points could be the same by translatingthe integer multi of reciprocal vector G= a The values ofk for free e is not limited and the energy is continuous
for the case of 1D, the state function and energy for the empty lattice model should be: 2 2 (0) (0) 1 , 2 ik r k k k e E L m = = where 0 indicates the solution with no perturbation. The relation between energy and wave vector is parabolic. Considering the requirement of symmetry, it is splitted into many parts. The energy of any two equivalent points could be the same by translating the integer multi of reciprocal vector 2 Gh a = The values of k for free e is not limited and the energy is continuous

E-K for the empty lattice model: End band Ist band 24 2nd band Ist band 2nd band K is limited in the FBZ for Bloche and the energy could be corresponding to many k When we consider the influences of the weaker periodical potential,the energy spectroscopy changes occurred at the border and the centre of the FBZ.The continuous parts were separated and a gap occurred.eg., the shape of the energy spectroscopy is modified at these points.In fact, the sharp parts were smoothed by the periodical potential in the empty lattice model.).In other parts,the influence of energy spectroscopy is little, and keep the basic parabolic shape
E-K for the empty lattice model: K is limited in the FBZ for Bloch e and the energy could be corresponding to many k When we consider the influences of the weaker periodical potential , the energy spectroscopy changes occurred at the border and the centre of the FBZ. The continuous parts were separated and a gap occurred. eg., the shape of the energy spectroscopy is modified at these points. In fact, the sharp parts were smoothed by the periodical potential in the empty lattice model.). In other parts, the influence of energy spectroscopy is little, and keep the basic parabolic shape
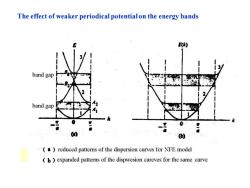
The effect of weaker periodical potential on the energy bands band gap band gap (a)reduced patterns of the dispersion curves for NFE model b expanded patterns of the dispwesion cureves for the same curve
The effect of weaker periodical potential on the energy bands
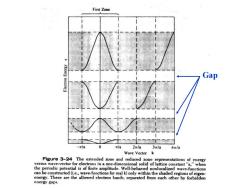
First Zone Gap -/a la2πla3πla4/a Wave Vector k Figure 3-24 The extended zone and reduced zone representations of energy versus wave-vector for electrons in a one-dimensional solid of lattice constant"a,"when the periodic potential is of finite amplitude.Well-behaved nonlocalized wave-functions can be constructed(i.e.,wave-functions for real k)only within the shaded regions of eigen- energy.These are the allowed electron bands,separated from each other by forbidden energy gaps
Gap

Perturbation method calculation:a 1D crystal L=Na 「-器e=vd U(x)=U(x+a) a is the lattice constant Fourier expansion: U(x)=U,+∑U,exp ,2πx a where U-U()dk average potential U =constant v.(es U minute term Potential is real term,not complex,so U(x)=U(x),UU
U x U x a ( ) = + ( ) a is the lattice constant Fourier expansion: ( ) 0 0 2 exp n n nx U x U U i a = + where ( ) 0 0 1 L U U x dx L = —— average potential =constant ( ) 0 1 2 exp L n nx U U x i dx L a = − L Na = Un minute term Potential is real term, not complex,so U(x)=U* (x), Un * =U-n 。 Perturbation method calculation: a 1D crystal ( ) ( ) ( ) 2 2 2 2 d U x x E x m dx − + = U

5.3.1.Nondegenerate perturbation H4=E(k)4H=- h2 d2 mdr+U(x) 品+-. 、 =H。+H n≠( H h2 d2 2m dx2 Zeroth order approximation r-22) Perturbationterm expand E(k)and v(k) E(k)=E0+E+E2+. 4=g0)+y0+y2)+
5.3.1. Nondegenerate perturbation ( ) H E k k k = ( ) 2 2 2 d 2 d H U x m x = − + 2 2 2 0 0 0 d 2 exp 2 d n n nx U U i H H m x a = − + + = + 2 2 0 0 2 d 2 d H U m x = − + Zeroth order approximation 0 2 exp n n nx H U i a = Perturbation term expand E(k) and (k) ( ) (0) (1) (2) E k E E E = + + + k k k (0) (1) (2) k k k k = + + +

Substitute it in the Schrodinger equation Hw=E How+H'vEw+Eo How +Hv=EE+E HEZeroth order approximation 2k2 Energy eigenvalue Let Uo=0 2m = 1 The corresponding wave function e Orthogonal normalization: ∫yery9=k1k)=d The 1st order perturbation eq H"+Hy°=E0+Ey0
Substitute it in the Schrödinger equation (0) (0) (0) H E 0 k k k = (1) (0) (0) (1) (1) (0) H H E E 0 k k k k k k + = + (2) (1) (0) (2) (1) (1) (2) (0) H H E E E 0 k k k k k k k k + = + + Zeroth order approximation (0) (0) (0) H E 0 k k k = Energy eigenvalue 2 2 2 2 (0) 0 2 2 k k k E U m m = + = The corresponding wave function (0) 1 ikx k e L = Orthogonal normalization: (0) (0) 0 L k k k k dx k k = = The 1st order perturbation eq (1) (0) (0) (1) (1) (0) H H E E 0 k k k k k k + = + Let U0=0

assume "-∑a"y9 ∑a"Ey0+Hy=E∑ap°+Ew° Lef-handed multiplicationrespectively and then integral aE0+Hk=Ega0+Eδ if k'=k E=H=∫*H'yk=kHlk) -e[Σ4,m2a产0 ifk≠k a E-E because E(1)=0,we need the second perturbation eq for the determination of perturbation energy
assume (1) (1) (0) k = a (1) (0) (0) (0) (0) (1) (0) (1) (0) k k k k a E H E a E + = + Left-handed multiplication respectively and then integral (0) k (1) (0) (0) (1) (1) k k k k k k k k k a E H E a E + = + if k’ = k (1) (0) (0) 0 L E H H dx k H k k kk k k = = = (1) 0 0 1 2 exp 0 L ikx ikx k n n nx E e U i e dx L a − = = if k’ k (1) (0) (0) k k k k k H a E E = − because Ek (1)=0,we need the second perturbation eq for the determination of perturbation energy

assume aSubstitute it into the second perturbation eq A=E”+-+a 2m E-E0 + 2mU, 2m 以1时+名” K'=k+2πn a 1得
assume (2) (2) (0) k = a Substitute it into the second perturbation eq 2 2 2 (0) (2) (0) (0) 2 k k k k k k k k k k H E E E m E E = + = + − 2 2 2 2 0 2 2 2 2 2 2 n n k m U m n k k a = + − + (0) (1) (0) (0) (0) (0) k k k k k k k k k k k H E E = + = + − ( ) ( ) 2 2 2 2 0 1 2 exp 2 / 1 2 / ikx n n mU i nx a e L k k n a = + − + 2 n k k a = +
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.5 The symmetry of bands.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4(supplement - Thermal Expansion of Glass).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.6 Anharmonic Effects 4.7 Equation of states for Lattice 4.8 Experimental methods for the determinations of lattice vibration spectroscopy.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.1 general background and approximations 5.2 Bloch’s Theorem.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.5 Heat capacity of the lattice.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 4 lattice dynamics and lattice capacity 4.1 Normal Modes of Vibration 4.2 Density of States 4.3 Harmonic approximation and normal mode coordinates 4.4 phonon.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3.1 General crystal binding 3.2 typical binding.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3(Supplement - Rules of crystal binding).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 3 Interatomic Bonding 3.3 The cohesive energy for ionic crystal.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice(2.1-2.5).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice 2.6 X-Ray Diffraction Methods 2.7 Applications of XRD.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 2 Wave Diffraction & the Reciprocal Lattice(supplement - Review & Overview of X-Rays).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.9 Elements of Symmetry 1.10 Space groups 1.11 7 crystal system and 14 Bravis Lattice.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure(Supplement - microstructure and crystal system).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Introduction.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.1 Elementary Crystallography 1.2 Crystal Structure ≡ Lattice + Basis 1.3 Lattice Translation Vectors 1.4 Non-Bravais Lattices 1.5 Wigner-Seitz Method.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.6 typical crystal structure.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 1 Crystal Structure 1.7 Lattice Sites in a Cubic Unit Cell 1.8 crystal plane and miller index.ppt
- 《固体物理学》课程教学资源(参考资料)词汇汉英对照.pdf
- 《固体物理学》课程授课教案(讲义)第五章 能带理论.pdf
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.4 Tight Binding Approximation(TBA).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 6 Electron motion in the crystal 6.1 The quasi-classical description of Bloch electrons 6.2. Electron quasi-momentum 6.3 The accelerated velocity and effective mass.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 6 Electron motion in the crystal 6(supplement - a more concise description of quasi-momentum).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 6 Electron motion in the crystal 6.4 The electron motion in a constant electric field 6.5 Band structure of conductor, insulator and semiconductor.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 7 The electronic theory of metal(supplement - Sommerfield expansion).ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 7 The electronic theory of metal 7.1 Fermi statistics and the heat capacity of electron 7.2 Work function and contact potential.ppt
- 《固体物理学》课程教学课件(PPT讲稿)Chapter 5 band theory 5.6 Density of states(DOS)and Fermi surface 5.7 the electrons in the crystal 5.8 the experimental results for DOS.ppt
- 《近代物理实验》课程教学大纲.doc
- 《近代物理实验》课程教学资源(PPT课件讲稿,共五部分).ppt
- 《工程光学》课程教学大纲 Engineering Optics.doc
- 安徽大学:《工程光学》课程授课教案(讲义,共十三章,授课教师:李桂华).doc
- 《工程光学》课程实验指导书(共六个实验).doc
- 《量子力学》课程教学课件(讲稿)Chapter 4 态和力学量的表象 The representation for the states and dynamical variable.pdf
- 《量子力学》课程教学课件(讲稿)Chapter 1 绪论 Quantum mechanism(量子力学的诞生).pdf
- 《量子力学》课程教学课件(讲稿)Chapter 2 波函数和薛定谔方程 The wave function and Schrödinger Equation.pdf
- 《量子力学》课程教学课件(讲稿)Chapter 3 量子力学中的力学量 The Dynamical variable in Quantum Mechanism.pdf
- 《量子力学》课程教学课件(讲稿)Chapter 6 散射 Scattering.pdf
- 《量子力学》课程教学课件(讲稿)Chapter 5 微扰理论近似方法 Approximation(本征值问题的似解).pdf
- 《量子力学》课程教学课件(讲稿)Chapter 7 自旋与角动量、全同粒子体系 Spin and undistinguished similar particles.pdf
- 《量子力学》课程教学资源(习题解答)第七章 自旋与角动量、全同粒子体系.doc
