《固体物理学》课程教学课件（PPT讲稿）Chapter 1 Crystal Structure 1.6 typical crystal structure

1.6 typical crystal structure Body Centered Cubic Packing Space Group Im3m a=4r/(32 Atom Site x M 2a 0 0 0 *r=metallic radius Representative Examples Fe(a=2.8664A Cr(a=2.8846A) Mo(a=3.1469A W(a=3.1650A) Cubic or Hexagonal Close Packing Coordination Number =12 Ta(a=3.3026A) Packing Efficiency 74% Ba(a=5.019A) Body Centered Cubic Packing Coordination Number 8 Packing Efficiency 68%

1.6 typical crystal structure

1).bcc lattice (Li,Na,K,Rb,Cs.etc) One possible choice of primitive vectors lattice a constant a(+方-动 属-++头 A conventional unit cell, 属(-+头 (nonprimitive) Note:A bcc lattice is a simple lattice. But we can also treat it as a cubic lattice with a 2-point basis! (to take advantage of the cubic symmetry

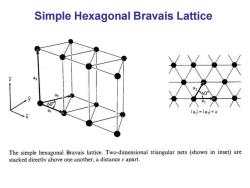
Simple Hexagonal Bravais Lattice 60 lal=la=a The simple hexagonal Bravais lattice.Two-dimensional triangular nets (shown in inset)are stacked directly above one another,a distance c apart

Simple Hexagonal Bravais Lattice

Conventional Primitive Unit Cells Points of Primitive Cell Hexagonal Bravais Lattice w Primitive Cell Conventional Cell Fractional coordinates of lattice points in conventional cell: 100,010,110,101,011 111,000,001 b

Conventional & Primitive Unit Cells Hexagonal Bravais Lattice Primitive Cell = Conventional Cell Fractional coordinates of lattice points in conventional cell: 100, 010, 110, 101, 011 111, 000, 001 Points of Primitive Cell a b c

Hexagonal Close Packed (HCP)Structure: (A Simple Hexagonal Bravais Lattice with a 2 Atom Basis) Figure 22 The hexagonal close-packed struc- ture.The atom positions in this structure do The HCP lattice is not a Bravais not constitute a space lattice.The space lattice is simple hexagonal with a basis of two identi- lattice,because the orientation of cal atoms associated with each lattice point. the environment of a point varies The lattice parameters a and c are indicated, where a is in the basal plane and c is the mag- from layer to layer along the c-axis. nitude of the axis ag of Fig.14

Hexagonal Close Packed (HCP) Structure: (A Simple Hexagonal Bravais Lattice with a 2 Atom Basis) The HCP lattice is not a Bravais lattice, because the orientation of the environment of a point varies from layer to layer along the c-axis

Hexagonal Close Packed (HCP)Lattice Hexagonal Close Packed and related structures Crystal cla Crystal cla Crystal clu He 1.633 1.861 1.594 Be 1.581 d 1.886 d 1.592 Mg 1.623 Co 1.622 Lu 1.586 1.586 Y 1.570

Hexagonal Close Packed (HCP) Lattice

3).hcp structure (=simple hexagonal lattice a 2-point basis.) e.g.Be,Mg.etc.complex lattices 2 overlapping "simple hexagonal lattices" d(dxa,)ae nt basis For ideal hcp structure Figure 22 The hexagonal close-packed struc Figure 23 The primitive cell has a,=ag ture.The atom positions in this structure do with an included angle of 120.The e axis (or not constitute a space lattice.The space lattice snormal to the plane of a and The /8 is simple hexagonal with a basts of two identi- ideal hep structure hase=1.633 The two C cal atoms associated with each lattice point. atoms of one basis are shown as solid cireles. One atom of the basis is at the origin:the a N =1.633 The lattice parameters a and c are indicated where a is in the basal plane and c is the mag. other atom is at which means at the posi nitude of the axis a of Fig 14. tion r ia+a:+las. >Primitive vectors:a,a2,c [c=2av(2/3)for hcp] >The 2 atoms of the basis are located at d,=0 and atd2=(2/3)a1+(13)a2+(1/2)c

a a a a c 2 1 2 3 2 3 (  ) =    1.633 3 8 = = a c For ideal hcp structure

Hexagonal Close Packed (HCP)Lattice Bravais Lattice: a=b Hexagonal Lattice Angle between a b=120 He,Be,Mg,Hf,Re c=1.633a, (Group IⅡelements) basis: ABABAB Type of Stacking (0,0,0)(2/3a,1/3a,1/2c)

Crystal Structure 8 Bravais Lattice : Hexagonal Lattice He, Be, Mg, Hf, Re (Group II elements) ABABAB Type of Stacking a = b Angle between a & b = 120° c = 1.633a, basis: (0,0,0) (2/3a ,1/3a,1/2c) Hexagonal Close Packed (HCP) Lattice

Close Packed Array of Spheres The gray spheres represent a 2D Close Packed Array. In 3D the next layer of spheres could sit on the depressions marked in red (B)or those marked in blue (C). AB Stacking AC Stacking

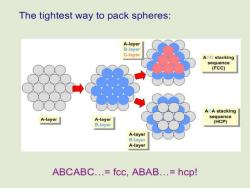
The tightest way to pack spheres: A-layer B-layer C-layer ABC stacking sequence (FCC) ABA stacking A-layer A-layer sequence (HCP) B-layer A-layer B-layer A-layer ABCABC.=fcc,ABAB.=hcp!